En la primera parte, analizamos el álgebra externa y nos dimos cuenta de que los vectores normales en 3D se pueden interpretar como bivectores. Para transformar bivectores, en el caso general, se necesita una matriz diferente a la que transforma los vectores ordinarios. Usando la base canónica para bivectores, descubrimos que esta es la matriz adjunta , que es proporcional a la transpuesta inversa. Este razonamiento explica al menos parcialmente por qué las normales son transformadas por la matriz transpuesta inversa.
Pero algunas cuestiones quedaron ocultas.
Consideramos matrices adjuntas, pero no mostramos cómo se relacionan con la prueba algebraica de que para transformar la ecuación planase necesita una matriz transpuesta inversa. La proporcionalidad entre las matrices fue, en cierto sentido, inverosímil.
Además, vimos que -vectores del álgebra externa proporcionan a los objetos geométricos vectoriales una interpretación natural, en la que contienen unidades de longitud, área y volumen, que cambian en consecuencia al escalar. Pero no encontramos nada como esto para las densidades: unidades inversas a la longitud, el área y el volumen.
En este artículo, veremos otro concepto geométrico que será necesario para completar la pintura. La fusión de este nuevo concepto con el álgebra externa ya estudiada aclarará y resolverá las cuestiones restantes.
Funciones como vectores
, . , , , .
: , ,
. — , … , ? ?
, . , (). , , : ( ). .
! . , : . , , .
: ( , ) — . . , , "". .
. , .
, .
, , . , .
( : , . !)
(3D) (2D), / , . :
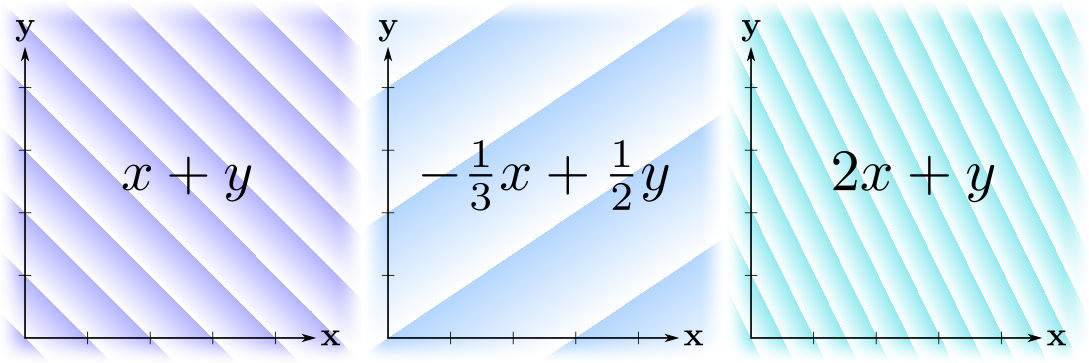
— . . , "́" ( ́ ) , .
, . , .
— — , : ( ) . . ( ) .
, — , , . - , , . , , .
, . . , — — , :
, — !
, : . .
, , , . , , "" . , — , … .
: . — , — . , . , — , .
:
, " " , .
. , , . :
. :
.
, , , . , . , . .
:
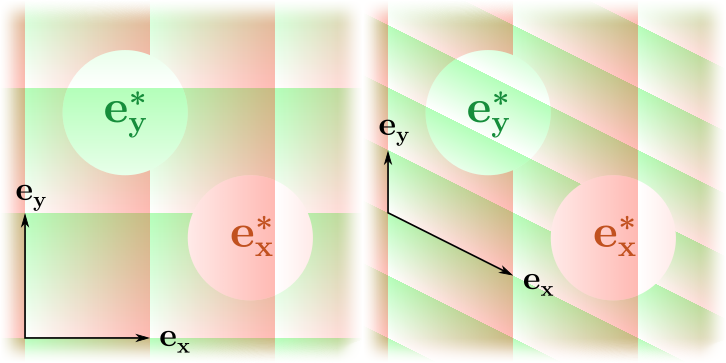
:
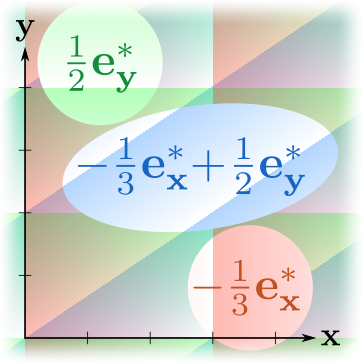
. :
, ( ), , , .
! "" ( ), ( 3D), ( ). !
— , . ?
: . , . : - . ( , ).
: , , . :
, , .
, . " " : .
, , . , . .
, . , ?
, , . , :
! , . "" "" . , , !
, . , (, , , //) - . ( ), " "" ?"
"". , , - , . .
. , , — , . .
. , :
:

? : .
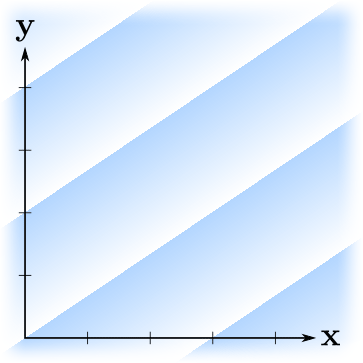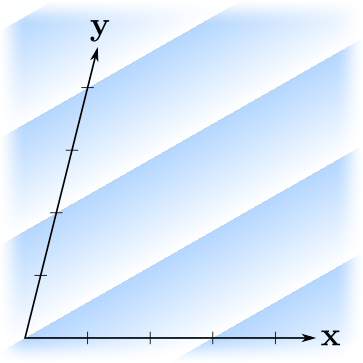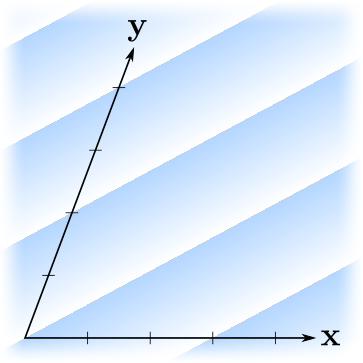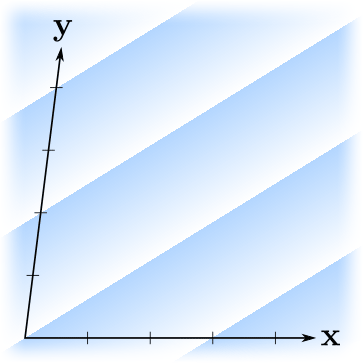
, ? . , — . ?
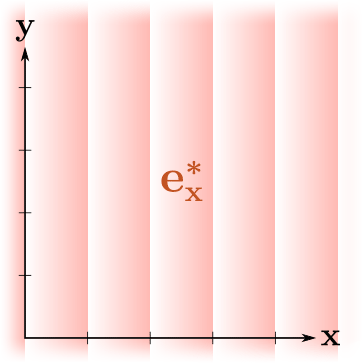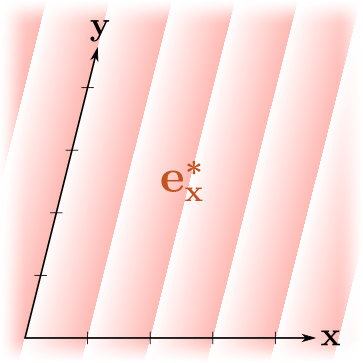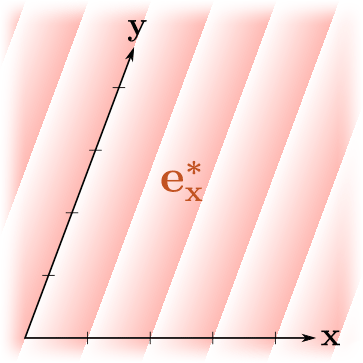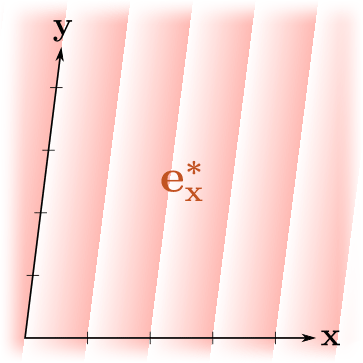
, ! , , , "" , . , .
, . , , , ,
!
, , . , , ( ), . :
.
, , .
?
, — 2D 3D. , , :
.
, , . :
, .
, , .
. , , , ? ?
, . " " , , . , : , . : , — .
Esto es todo lo que quería hablar sobre las transformaciones de los vectores normales, pero algunas preguntas más permanecen en el limbo. Al final de la primera parte, hice una pregunta sobre los grados negativos de escala. Ahora tenemos menos el primer grado, pero ¿qué pasa con -2 y -3? Para entender esto, tenemos que combinar álgebra externa y espacios duales, lo que haremos en la tercera parte.