Existe un hecho tan misterioso acerca de las transformaciones lineales: algunas de ellas, a saber, el escalado y la traducción no uniformes, por alguna razón distinguen entre vectores "ordinarios" y normales. Cuando transformamos un vector "normal" por una matriz, entonces las normales por alguna razón necesitan ser transformadas por una matriz transpuesta inversa. ¿Cómo entender esto?

Con la ayuda de cálculos simples, puede asegurarse de que la matriz transpuesta inversa preserva la perpendicularidad de las normales a sus planos tangentes. Hasta cierto punto, esta prueba es suficiente, pero se pierde una historia más profunda e interesante sobre la geometría detrás de todo. Esta es la historia que quiero contar en los próximos artículos.

Unidades y escala

Aquí hay un resumen rápido antes de profundizar en el corazón del artículo. Considere un buen escalado uniforme antiguo (un factor en todos los ejes). Es difícil pensar en una transformación más inocua: es solo la multiplicación de todos los vectores por el mismo número.

Pero tras una inspección más cercana, algo no del todo trivial está sucediendo aquí. Ciertas cantidades llevan consigo "dimensiones" o "unidades" físicas como longitudes, áreas y volúmenes. Al escalar, estos valores cambian de acuerdo con sus unidades. Algunos valores son generalmente "adimensionales" y no cambian cuando se escalan.

Como ejemplo, enumeremos todos los posibles comportamientos de las unidades al escalar en un espacio tridimensional. Denotamos el factor de escala como $a>0$ . Entonces:

Los números adimensionales no cambian, en otras palabras, se multiplican por $a^0$ .
Las longitudes se multiplican por $a$ .
Las áreas se multiplican por $a^2$ .
$a^3$ .

: , :
$1\over{a}$ .
$1\over{a^2}$ .
$1\over{a^3}$ .

, , . 3D- , , , .

, ( ) , : , ( ), , - . , -3 3. , $k$ - , $a^k$ .

( $\pm 4$ , . , 3D.)

, - . ? ? ? -, .

, . , . , Geometric Algebra for Computer Science. .

— , , , , . $k$ -, $k$ — . , — . .

— ( ) , . , , . , .

, , . , . , . , , , .

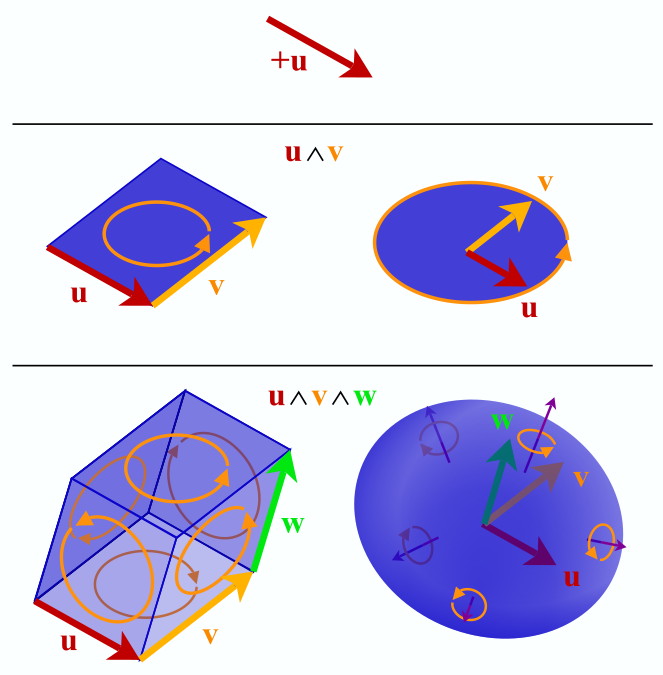
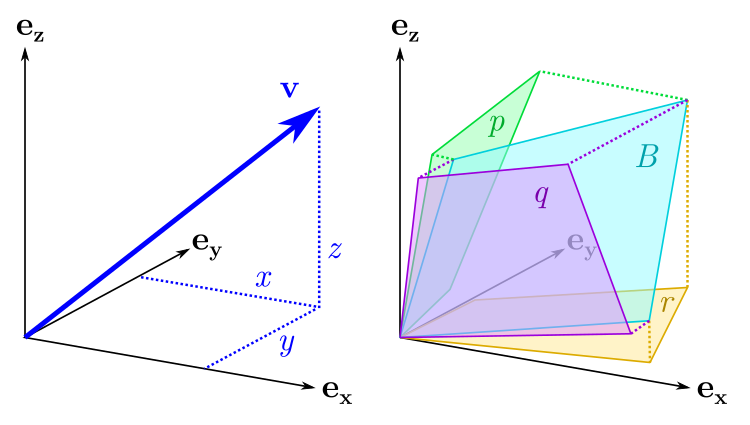
imagen

, — , , . , , , , .

. , , . , , "" "", "" "". , , .

́ , . , $k$ - . .

$k$ -

, . $v=(x, y, z)$ , , $v$ :

v = x e_{x} + y e_{y} + z e_{z}

$v=x{\bf e_x}+y{\bf e_y}+z{\bf e_z}$

${\bf e_x}$ , ${\bf e_y}$ , ${\bf e_z}$ , $y$ , $z$ . $B$ :

B = p e_{y z} + q e_{z x} + r e_{x y}

$B=p{\bf e_{yz}}+q{\bf e_{zx}}+r{\bf e_{xy}}$

${\bf e_{xy}}$ — , $xy$ . ${\bf e_{yz}}$ ${\bf e_{zx}}$ . , , . " " $(p, q, r)$ , .

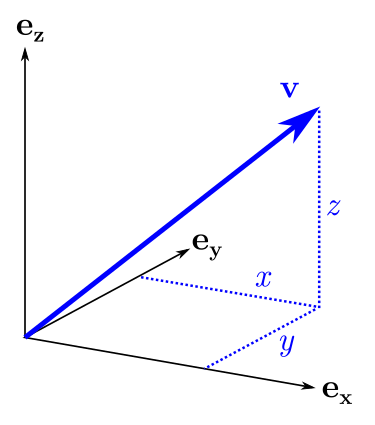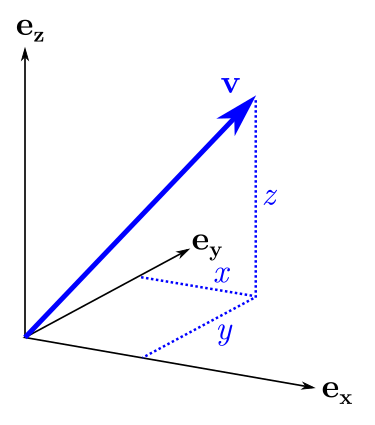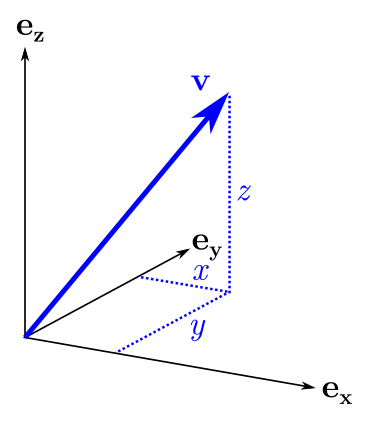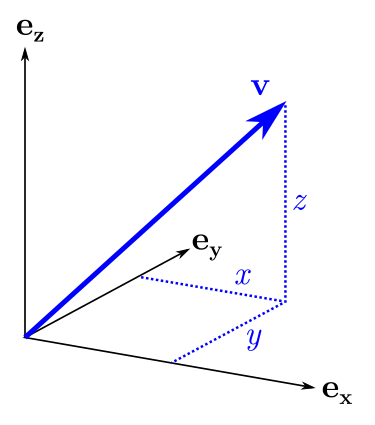
imagen

:

T = t e_{x y z}

$T=t{\bf e_{xyz}}$

, 3D , : "" $(xyz)$ . — ${\bf e_{xyz}}$ .

, : ( 1), ( 2) ( 3). 0. , , , $\wedge$ . , , :

e_{x} \land e_{y} = e_{x y}

${\bf e_x}\wedge{\bf e_y} = {\bf e_{xy}}$

, , . , ( ).

, "" . , , . , .

, , .

e_{x} \land e_{y} \land e_{z} = e_{x y} \land e_{z} = e_{x y z}

${\bf e_x}\wedge{\bf e_y}\wedge{\bf e_z} = {\bf e_{xy}}\wedge{\bf e_z}={\bf e_{xyz}}$

" ", , , .

, . . $a$ :

(a u) \land v = u \land (a v) = a (u \land v)

$(au)\wedge v=u\wedge (av) = a(u\wedge v)$

, . $u, v$ :

u \land v = - (v \land u)

$u\wedge v=-(v\wedge u)$

. -, : $v\wedge v=0$ . , . , $u\wedge v=0$ $u$ $v$ . , $u\wedge v\wedge w=0$ $u, v, w$ .

3 . , .

$k$ -

, , — , — . ?

, , - . $a>0$ , $a, a^2, a^3$ . , , .

, :

v \mapsto M v

$v\mapsto Mv$

[\begin{matrix} x \\ y \\ z \end{matrix}] \mapsto [\begin{matrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \end{matrix}] [\begin{matrix} x \\ y \\ z \end{matrix}] = [\begin{matrix} a x \\ a y \\ . a z \end{matrix}] = a v

$\begin{bmatrix} x \\ y \\ z \end{bmatrix} \mapsto \begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} ax \\ ay \\. az \end{bmatrix} = av$

$v$ , $x, y, z$ , , $a$ , , .

? ( ), . . , , :

\begin{aligned} B & = u \land v \\ (u \land v) & \mapsto (M u) \land (M v) \\ = (a u) \land (a v) \\ = a^{2} (u \land v) \\ = a^{2} B \end{aligned}

$\begin{aligned} B &= u \wedge v \\ (u \wedge v) &\mapsto (Mu) \wedge (Mv) \\ &= (au) \wedge (av) \\ &= a^2 (u \wedge v) \\ &= a^2 B \end{aligned}$

! , $a$ , $a^2$ , .

, . , - $a^3$ . :

\begin{aligned} T & = (u \land v \land w) \\ (u \land v \land w) & \mapsto (M u) \land (M v) \land (M w) \\ = (a u) \land (a v) \land (a w) \\ = a^{3} (u \land v \land w) \\ = a^{3} T \end{aligned}

$\begin{aligned} T &= (u \wedge v \wedge w) \\ (u \wedge v \wedge w) &\mapsto (Mu) \wedge (Mv) \wedge (Mw) \\ &= (au) \wedge (av) \wedge (aw) \\ &= a^3 (u \wedge v \wedge w) \\ &= a^3 T \end{aligned}$

. , ?

, . 3 $x$ , . :

M = [\begin{matrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]

$M = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

: $x$ 3, $y, z$ . , : , $x$ , $yz$ — .

imagen

? . , "" . $x$ , . : , $yz$ , , , $x$ , .

imagen

, . , , :

B = p e_{y z} + q e_{z x} + r e_{x y}

$B = p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}$

$M$ , . $M$ :

\begin{aligned} e_{y z} = e_{y} \land e_{z} & \mapsto (M e_{y}) \land (M e_{z}) = e_{y} \land e_{z} = e_{y z} \\ e_{z x} = e_{z} \land e_{x} & \mapsto (M e_{z}) \land (M e_{x}) = e_{z} \land 3 e_{x} = 3 e_{z x} \\ e_{x y} = e_{x} \land e_{y} & \mapsto (M e_{x}) \land (M e_{y}) = 3 e_{x} \land e_{y} = 3 e_{x y} \end{aligned}

$\begin{aligned} {\bf e_{yz}} = {\bf e_y} \wedge {\bf e_z} \quad &\mapsto \quad (M{\bf e_y}) \wedge (M{\bf e_z}) = {\bf e_y} \wedge {\bf e_z} = {\bf e_{yz}} \\ {\bf e_{zx}} = {\bf e_z} \wedge {\bf e_x} \quad &\mapsto \quad (M{\bf e_z}) \wedge (M{\bf e_x}) = {\bf e_z} \wedge 3{\bf e_x} = 3{\bf e_{zx}} \\ {\bf e_{xy}} = {\bf e_x} \wedge {\bf e_y} \quad &\mapsto \quad (M{\bf e_x}) \wedge (M{\bf e_y}) = 3{\bf e_x} \wedge {\bf e_y} = 3{\bf e_{xy}} \end{aligned}$

: $\bf e_{yz}$ , $\bf e_{zx}$ $\bf e_{xy}$ 3, $x$ .

, $M$ $B$ :

B \mapsto p e_{y z} + 3 q e_{z x} + 3 r e_{x y}

$B \mapsto p \, {\bf e_{yz}} + 3q \, {\bf e_{zx}} + 3r \, {\bf e_{xy}}$

, , $B$ , :

[\begin{matrix} p \\ q \\ r \end{matrix}] \mapsto [\begin{matrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{matrix}] [\begin{matrix} p \\ q \\ r \end{matrix}] = [\begin{matrix} p \\ 3 q \\ 3 r \end{matrix}]

$\begin{bmatrix} p \\ q \\ r \end{bmatrix} \mapsto \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} p \\ q \\ r \end{bmatrix} = \begin{bmatrix} p \\ 3q \\ 3r \end{bmatrix}$

, , . : $M$ .

: $M$ :

M^{- T} = [\begin{matrix} \frac{1}{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]

$M^{-T} = \begin{bmatrix} \tfrac{1}{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

, — $M$ .

$\det M$ . ( $M$ , $\det M$ ). $M$ . , , !

— , . .

$n\times n$ . $i$ - $j$ - :

$n\times n$ $i$ $j$ . $(n-1)\times (n-1)$ .
.
$(-1)^{i+j}$ , $i+j$ . !

$n\times n$ , .

, ? $p \, {\bf e_{yz}}$ . $yz$ , , $M$ $y$ $z$ . $1,1$ $M$ $2\times2$ , $M$ $y$ $z$ . , , $yz$ !

- , ${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ , , $M$ . , , $M$ . , , .

( , . ${\bf e_{xz}}$ ${\bf e_{zx}}$ . .)

, , $n$ $(n-1)$ - . , $k$ - $(n-k)$ - , $n-k$ .

. . : 3D. , $(p, q, r)$ — $(x, y, z)$ !

. , . , $B$ :

B \land v = 0

$B\wedge v=0$

$v$ , $B$ , . , , , $B$ $v$ .

\begin{matrix} (p e_{y z} + q e_{z x} + r e_{x y}) \land (x e_{x} + y e_{y} + z e_{z}) = 0 \\ (p x e_{y z x} + q y e_{z x y} + r z e_{x y z}) = 0 \\ (p x + q y + r z) e_{x y z} = 0 \\ p x + q y + r z = 0 \end{matrix}

$\begin{gathered} (p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}) \wedge (x \, {\bf e_x} + y \, {\bf e_y} + z \, {\bf e_z}) = 0 \\ (px \, {\bf e_{yzx}} + qy \, {\bf e_{zxy}} + rz \, {\bf e_{xyz}}) = 0 \\ (px + qy + rz) {\bf e_{xyz}} = 0 \\ px + qy + rz = 0 \\ \end{gathered}$

. , , (, ${\bf e_{yz}} \wedge {\bf e_y} = 0$ ). $\bf e_{xyz}$ , , . . , $\bf e_{xyz}$ .

$(p, q, r)$ $(x, y, z)$ ! , $n\cdot v = 0$ $n=(p, q, r)$ .

, $(p, q, r)$ ${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ ${\bf e_x}, {\bf e_y}, {\bf e_z}$ . , . , . .

, - . — . ( ) " ".

, . , "" , . ? , , ? , , ( ). .

: , , -3 3. , $k$ - $k$ 0 a 3. Pero, ¿qué pasa con las unidades vectoriales con grados de escala negativos? ¿Existen? Si es así, ¿Que son?

En el próximo episodio, profundizaremos aún más y complicaremos aún más nuestra historia geométrica.

Normales y transposición inversa, parte 1: álgebra externa

Unidades y escala

$k$ -

$k$ -

More articles:

Normales y transposición inversa, parte 1: álgebra externa

Unidades y escala

kk-

kk-

More articles:

$k$ -

$k$ -