¿Qué? ¿Para qué?
¡Hola!
Me gustaría considerar un problema de geometría computacional, a saber, la construcción de un casco convexo en 3D . Como me parece, este no es ni el algoritmo más complicado ni el más simple, lo que sería muy interesante y útil de analizar.
Si nunca te has enfrentado a una tarea así, creo que te resultará interesante conocerla, ver de qué se trata.
Si acaba de escuchar algo sobre los cascos convexos, puede obtener más información sobre ellos.
Si eres un gurú de los cascos convexos, es posible que quieras escuchar de nuevo la solución a un problema interesante.
Contenido
- ¿Qué? ¿Para qué?
- ¿Qué es un casco convexo?
- Palabras comunes
- Descripción del algoritmo
- Asintóticos
- Implementación de algoritmos
- Plena aplicación
Expreso mi gratitud muji-4ok para obtener ayuda para escribir y editar el artículo.
¿Qué es un casco convexo?
El casco convexo de un conjunto X es el conjunto convexo más pequeño que contiene el conjunto X.
Estrictamente, pero no muy claro. Ahora intentaré decirte con un ejemplo:
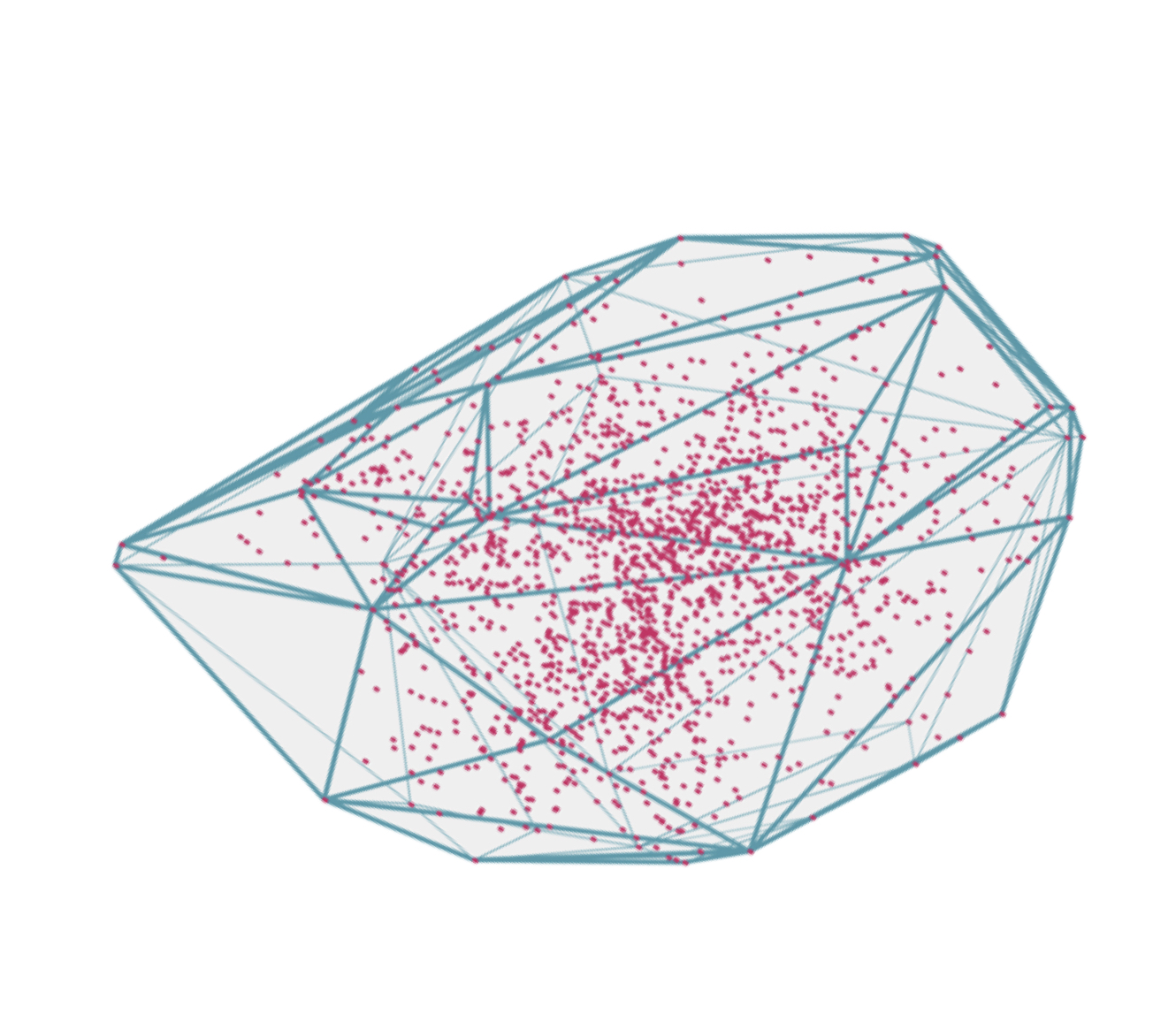
imagina un conjunto de puntos en un plano, y, digamos, queremos saber cuál es el número mínimo de puntos que deben estar conectados para que todo el conjunto de puntos restante se encuentre dentro de la superficie delineada. Este es el problema de encontrar el casco convexo mínimo.

2D
,
, , , , , , "" , .
, , , 3D . , .
: , ?
— .
— . , , : .
, , .
, ( ) " ".
, 4 . 3 .
, , .
, , 3d , . , .
1.
, , , , .
, .
Z. , , "" Z . XY , . . , . P, , "" — f.
, . Q, f ( prQ). , () {P, Q} {Q, prQ} — — . , Q , . Q .

. R, , P, Q R (0, 0, 1) . , f — XY. , , . , , R .
, , , , ( - ).
, P, Q, R .
-! , .
2.
, , , . , .
: , . , , , , () ( ), , . , , , , .
: , . : .
1. ? , . . E. , , E — R. ( E) , E R. , , , — .
2. , , " ", E , , E .
3. , , . , , . , , , .
4. , . , . , "" , .
5. , "" , .
6. , . , .
, ( ), 3D .
, , . , . N, H , O(NH). H 2N, O(N^2).
, , , O(NlogN), , . 2D , O(NlogN), , , , .
, , : .
, , , , , . C++.
. . , , -. - . ( , ).
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point (coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator- (const Point& other) const;
Point operator+ (const Point& other) const;
bool operator!= (const Point& other) const;
bool operator== (const Point& other) const;
};. 22 ( ).
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}( A — — - - AB AC):
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}( ):
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}:
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}, .
. , . , , , , . , , .
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false; // , ?
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)) :
first(first), second(second), flatness(flatness) {}
};Flatness — . 3 , ( ). — Another, . ( — if — .)
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two);
};Class .
class ConvexHull
{
struct Flatness;
struct Edge;
std::vector<Point> points_; //
std::vector<Flatness> verge_; //
std::vector<Edge> edges_; //
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull(); }
};
: Z ( , )
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}, :
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}. (-)
. , : . - , , .
:
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point; //
first_point = findMinZ();, Z. "".
double min_angle = 7; // 2pi, 7
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i) //
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;, .
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;, , XY, (0, 0, 1). .
( ), .
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
} :
:
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);: , . , : .
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}, , e , . , , is_closed = true, , , , — — , .
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id); // -1,
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} // #include <iostream>
#include <vector>
#include <cmath>
#include <stack>
#include <iomanip>
using coordinate = int64_t;
struct Point;
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22);
Point VectorProduct(const Point& A, const Point& B, const Point& C);
double GetLenghtVector(Point A, Point B);
double GetAngle(const Point& n1, const Point& n2);
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point(coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator-(const Point& other) const
{
return Point(x - other.x, y - other.y, z - other.z);
}
Point operator+(const Point& other) const
{
return Point(x + other.x, y + other.y, z + other.z);
}
bool operator!= (const Point& other) const
{
return (x != other.x || y != other.y || z != other.z);
}
bool operator== (const Point& other) const
{
return (x == other.x && y == other.y && z == other.z);
}
};
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}
//[AB, AC]
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}
//vector AB
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}
class ConvexHull
{
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two)
{
if ((one == first && two == second) || (one == second && two == first))
{
return third;
}
if ((one == first && two == third) || (one == third && two == first))
{
return second;
}
if ((one == third && two == second) || (one == second && two == third))
{
return first;
}
return -1; // error
}
};
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false;
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)):
first(first), second(second), flatness(flatness) {}
};
std::vector<Point> points_;
std::vector<Flatness> verge_;
std::vector<Edge> edges_;
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull();}
};
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id);
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} //
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point;
first_point = findMinZ();
double min_angle = 7;
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i)
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;
//
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
}
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}.