☁️ 👩🏻‍⚖️ ♣️ Problema de mochila en criptografía (problema de mochila en criptografía) 👨🏻‍🎨 ✍🏻 👨🏼‍💻

El problema de la mochila (problema de la mochila) en criptografía es el problema a partir del cual los criptógrafos estadounidenses Ralph Merkle y Martin Hellman desarrollaron el primer algoritmo de cifrado de clave pública.

Más adelante en el programa

Formulación del problema de la mochila (+ ¿por qué una mochila?)
Desafíos fáciles y difíciles
Ejemplos de
Historia

¿Qué es el cifrado de clave pública?

, , «», .

. , , , .

: , .

, - !

El primer algoritmo de clave pública general utilizó el algoritmo de mochila.

Según la definición de sistemas de claves públicas, se necesitan dos claves para cifrar (y descifrar) un mensaje con éxito. El destinatario "legal" del mensaje conoce la clave secreta

А

mientras el remitente posee otra clave pública

B

$B$ ...

¿Qué hacer si un atacante conoce una clave pública?

Hay una respuesta: la clave pública debe obtenerse de la clave secreta mediante una transformación ( función unidireccional )

f

$f$ con las siguientes dos propiedades:

$B = f(A)$ conociendo A, es fácil calcular la función en sí

$A = f^{-1} (B)$ , Y es difícil de calcular la función inversa

¿Qué es "fácil" y "difícil"?

.

«» , . ..

n

$n$ , —

t \propto n^{a}

$t \propto n^a$ ,

a

$a$ — . , .

«» . , , .

..

n

$n$ ,

t \propto 2 n

$t \propto 2n$ , , .

El problema de la mochila se formula de la siguiente manera

Dado un conjunto de (vector de mochila)

A = (a_{1}, . . ., a_{n})

$A = (a_1, ... , a_n)$ Es un conjunto ordenado de

n

$n$ (

n > 2),

$n > 2),$ números naturales distintos

a_{i}

$a_i$ ... Que haya un numero

k

$k$ - completo y positivo. La tarea es encontrar tal conjunto

a_{i}

$a_i$ para que en total den exactamente

k

$k$ ...

En la versión más famosa del problema de la mochila, se requiere averiguar si un par dado tiene

(A, k)

$(A , k)$ decisión. En la variante utilizada en criptografía, necesita esta entrada

(A, k)

$(A , k)$ construya una solución sabiendo que tal solución existe. Ambas opciones son NP-completas.

Analogía de la mochila

En el caso mas simple

k

$k$ denota el tamaño (capacidad) de la mochila y cada uno de los números

a_{i}

$a_i$ indica el tamaño (peso) de un artículo que se puede guardar en una mochila. La tarea es encontrar ese conjunto de elementos para que la

mochila esté completamente llena.

Es decir, imagina que tienes un juego de pesos 1, 6, 8, 15 y 24, necesitas empacar una mochila con un peso de 30.

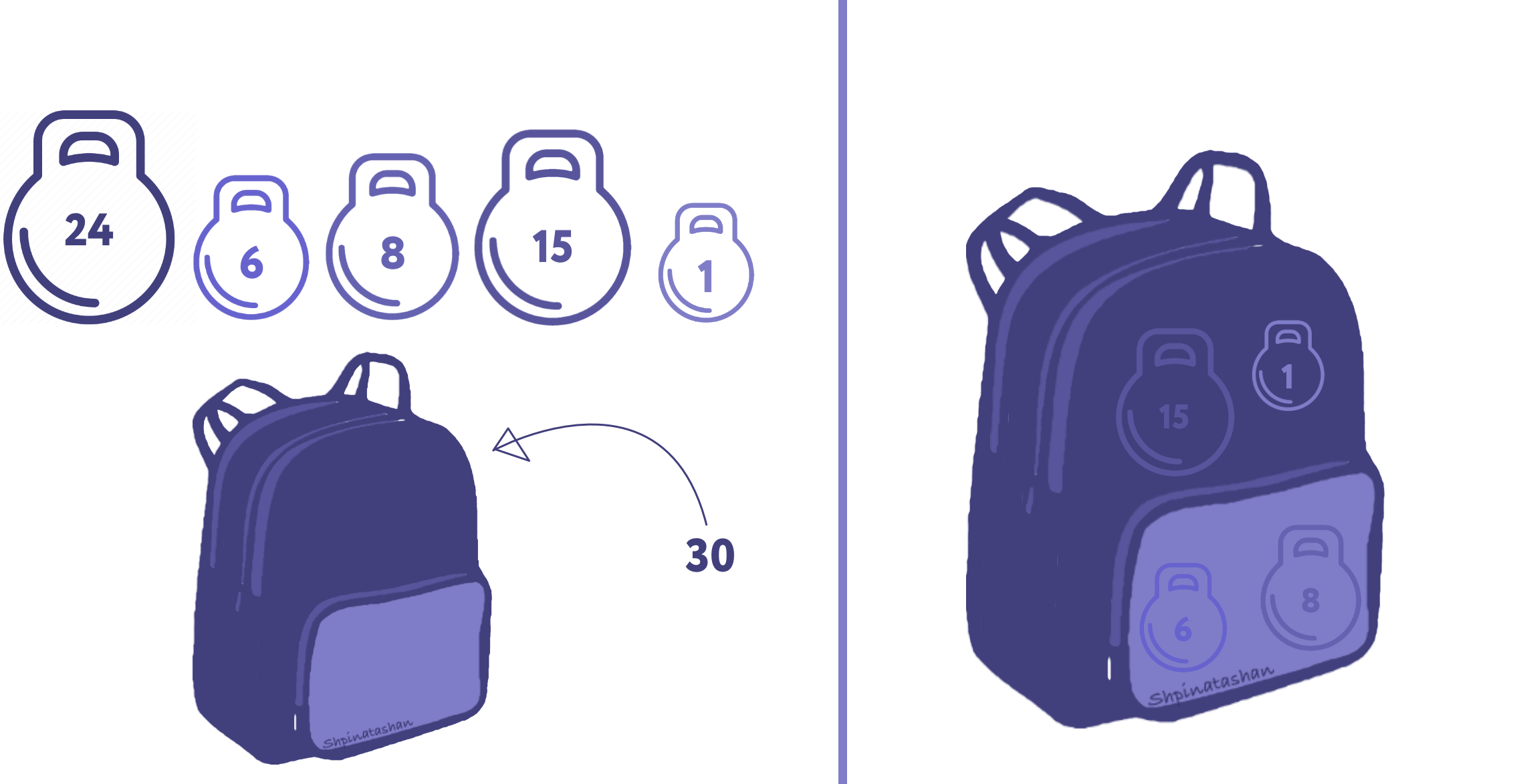
En principio, una solución siempre se puede encontrar mediante una búsqueda exhaustiva de subconjuntos

А

y comprobar cuál de sus sumas es

k

$k$ ... En nuestro caso, esto significa fuerza bruta.

2^{5} = 32

$2^5 = 32$ subconjuntos (incluido el conjunto vacío). Esto es bastante factible.

Pero, ¿y si hay varios cientos de números? $a_i$ ?

En nuestro ejemplo, n = 5, a fin de no complicar la presentación. En condiciones reales, un ejemplo tendrá, por ejemplo, 300

a_{i} - х

$a_i-$ ... El punto aquí es que no se conocen algoritmos que tengan una complejidad significativamente menor en comparación con la búsqueda exhaustiva. Buscar entre

2^{300}

$2^{300}$ los subconjuntos no se pueden procesar. De hecho, el problema de la mochila se conoce como NP-completo ... Los problemas NP-completos se consideran difíciles de calcular.

¿La función cumple con los requisitos especificados?

Definimos la función

f (x)

$f(x)$ de la siguiente manera. Cualquier número

0 \leq x \leq 2 n - 1

$0 ≤ x ≤ 2n − 1$ puede ser dado por una representación binaria de

n

$n$ bits, donde se añaden ceros a la izquierda si es necesario. Ahora definamos

f (x)

$f(x)$ como un número obtenido de

A

$A$ resumiendo todo eso

a_{i}

$a_i$ que el bit correspondiente en notación binaria

x

$x$ es igual a 1.

Es decir,

f (1) = f (0 . . . 001) = a_{n}

$f(1) = f(0 . . . 001) = a_n$

f (2) = f (0 . . . 010) = a_{n - 1}

$f(2) = f(0 . . . 010) = a_{n−1}$

f (3) = f (0 . . . 011) = a_{n - 1} + a_{n}

$f(3) = f(0 . . . 011) = a_{n−1} + a_n$

. . .

$...$

Función

f (х)

$f( )$ estaba determinado

n -

$n-$ conjunto

A

$A$ ... Obviamente, si somos capaces de calcular

x

$x$ de

f (x)

$f(x)$ , entonces prácticamente al mismo tiempo se resolverá el problema de la mochila:

x

$x$ su representación binaria se calcula inmediatamente, lo que a su vez da los componentes del conjunto

A

$A$ incluido en la suma de

f (x)

$f(x)$ ... Por otro lado, el cálculo

f (x)

$f(x)$ de

x

$x$ es ligero. Dado que el problema de la mochila es NP-completo,

f (x)

$f(x)$ es un buen candidato para una función unidireccional. Por supuesto, hay que exigir que $n$ era lo suficientemente grande, no digas menos $200$ ...

Cifrado

Texto sin formato

(. plain text) — , , . ( ).

Puede cifrar de dos formas:

El cifrado del mensaje se obtiene elevando los elementos de este vector mochila a la potencia de los bits correspondientes del mensaje cifrado y luego multiplicando todos los resultados, es decir, si $A = (2,3,5)$ y el mensaje $(100)$ , entonces el cifrado será el número $2^1*3^0*5^0=2$ ... Esta es una forma multiplicativa .
El cifrado del mensaje se obtiene multiplicando los elementos de este vector de mochila por los bits correspondientes del mensaje cifrado y luego sumando todos los resultados, es decir, si $A = (2,3,5)$ y el mensaje $(100)$ , entonces el cifrado será el número $2^ *1+3^ *0+5^ *0= 2$ ... Este método se llama aditivo .

Ejemplo

Para cifrar texto sin formato en representación binaria, se divide en bloques de longitud

n

$n$ (por ejemplo, puede representar el peso 30 con el binario 11110). Se cree que uno indica la presencia de un artículo en la mochila y el cero indica su ausencia.

El cifrado de mochila proporciona un buen enfoque para crear claves públicas y privadas, donde la clave privada es fácil de usar y la clave pública es difícil de descifrar.

Entonces, podemos crear un sistema donde: el problema "difícil" es la

clave pública , porque con él, puede cifrar fácilmente y es imposible descifrar el mensaje.

una clave privada : el problema "fácil" servirá como usándolo, puede descifrar fácilmente el mensaje. Sin la clave privada, tienes que resolver el "difícil" problema de la mochila.

Problema "fácil"

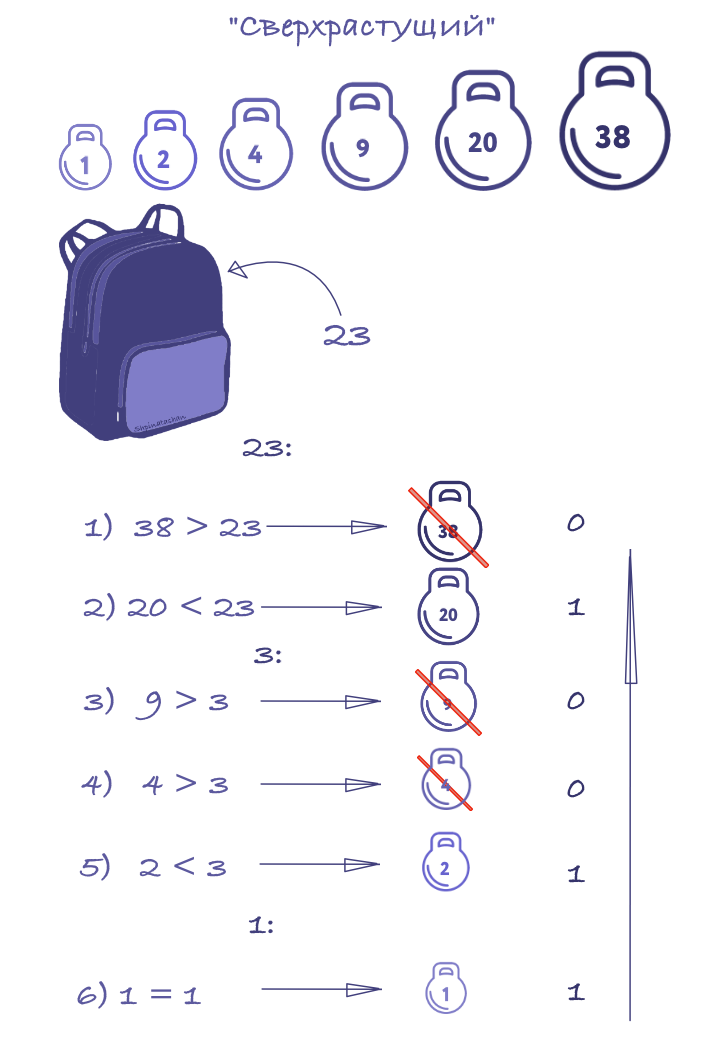
Vector de mochila super creciente

A = (a_{1}, . . ., a_{n})

$A=(a_{1},...,a_{n})$ ,

Σ_{i = 1}^{j - 1} a_{i} < a_{j}

$Σ_{i=1}^{j-1} a_{i} < a_{j}$

j = 2, . . ., n

$j=2,...,n$ , . .

Para los vectores sverhrastuschih, el problema de la mochila se puede resolver fácilmente. Aquellos. Mochila fácil de montar.

Tomemos un ejemplo:

Algoritmo

.

, , . , .
.
(1)-(2) .

, .

"Problema dificil

Es mucho más difícil descifrar el problema de una mochila no demasiado grande .

Merkle y Hellman crearon un algoritmo, que utiliza una mochila de clave privada de gran tamaño y una mochila de clave pública no demasiado grande.

Hicieron esto tomando la tarea de la mochila de gran tamaño y transformándola en una tarea que no es demasiado grande.

(Merkle y Hellman, utilizando aritmética modular, idearon una forma de transformar una mochila "ligera" en una "dura").

Crear una clave pública

Varios conceptos importantes

$(x, mod m)$ $x$ $m$ ,

$x$ — , $m > 1$ , [x/m] — ,
$x = (x, m o d m) + [x / m] * m$
$x = (x, mod m) + [x/m]*m$

$A$ , $m > max A$ $t < m$ , $(t, m) = 1$ .

$B = (b_1, . . . , b_n)$ , $b_i = (ta_i, modm)$ , $i = 1, . . . , n$ , , B A m t , , $(m, t)$ .

$(t, m) = 1$

$t^{−1} = u$ , ,

$t u \equiv 1 (m o d m)$
$tu ≡ 1 (mod m)$

$1 ≤ u < m$ . , $A$ $B$

$m, u$ .

$m > max A$

$m > Σ_{i=1}^{n} a_{i}$ , , $B$ $A$ $m, t$ .

— , , , .

El creador del criptosistema elige tal sistema

A, t, m, B

$A, t, m, B$ ese vector

A

$A$ está creciendo mucho, y

B

$B$ obtenido de

A

$A$ fuerte multiplicación modular con respecto a

m, t

$m, t$ ... Vector

B

$B$ expandido como clave de cifrado y bloques binarios de longitud

n

$n$ enviado al diseñador como números

β

$β$ Obtenido por vector

B

$B$ ...

El interceptor de mensajes debe resolver el problema de la mochila para ingresar

(B, β)

$(B, β)$ ... El creador del criptosistema calcula

α = (u β, m o d m)

$α = (uβ, modm)$

y resuelve el problema de la mochila para entrar

(A, α)

$(A, α)$ ... Por qué funciona todo esto se

muestra en el siguiente lema.

Lema . Pretendamos que

A = (a_{1}, . . ., a_{n})

$A = (a_1, . . . , a_n)$ vector y vector super creciente

B

$B$ derivado de

A

$A$ fuerte multiplicación modular con respecto a

m, t

$m, t$ ... Supongamos además que

u \equiv t^{- 1} (m o d m)

$u ≡ t^{−1} (mod m)$ ,

β

$β$ - un número natural arbitrario y

α = (u β, m o d m)

$α = (uβ,modm)$ ... Entonces las siguientes afirmaciones son verdaderas.

(i) El problema de la mochila

(A, α)

$(A, α)$ se puede resolver en tiempo lineal. Si existe una solución, entonces es única.

(ii) El problema de la mochila

(B, β)

$(B, β)$ tiene como máximo una solución.

(iii) Si hay una solución para ingresar

(B, β)

$(B, β)$ , entonces coincide con la única solución de entrada

(A, α)

$(A, α)$ ...

prueba (p. 104)

Ejemplo

Considere una secuencia de supercrecimiento; por ejemplo, {1, 2, 4, 10, 20, 40}. El módulo debe ser mayor que la suma de todos los números en la secuencia, por ejemplo 110. El multiplicador no debe tener divisores comunes con el módulo. Así que escojamos 31.

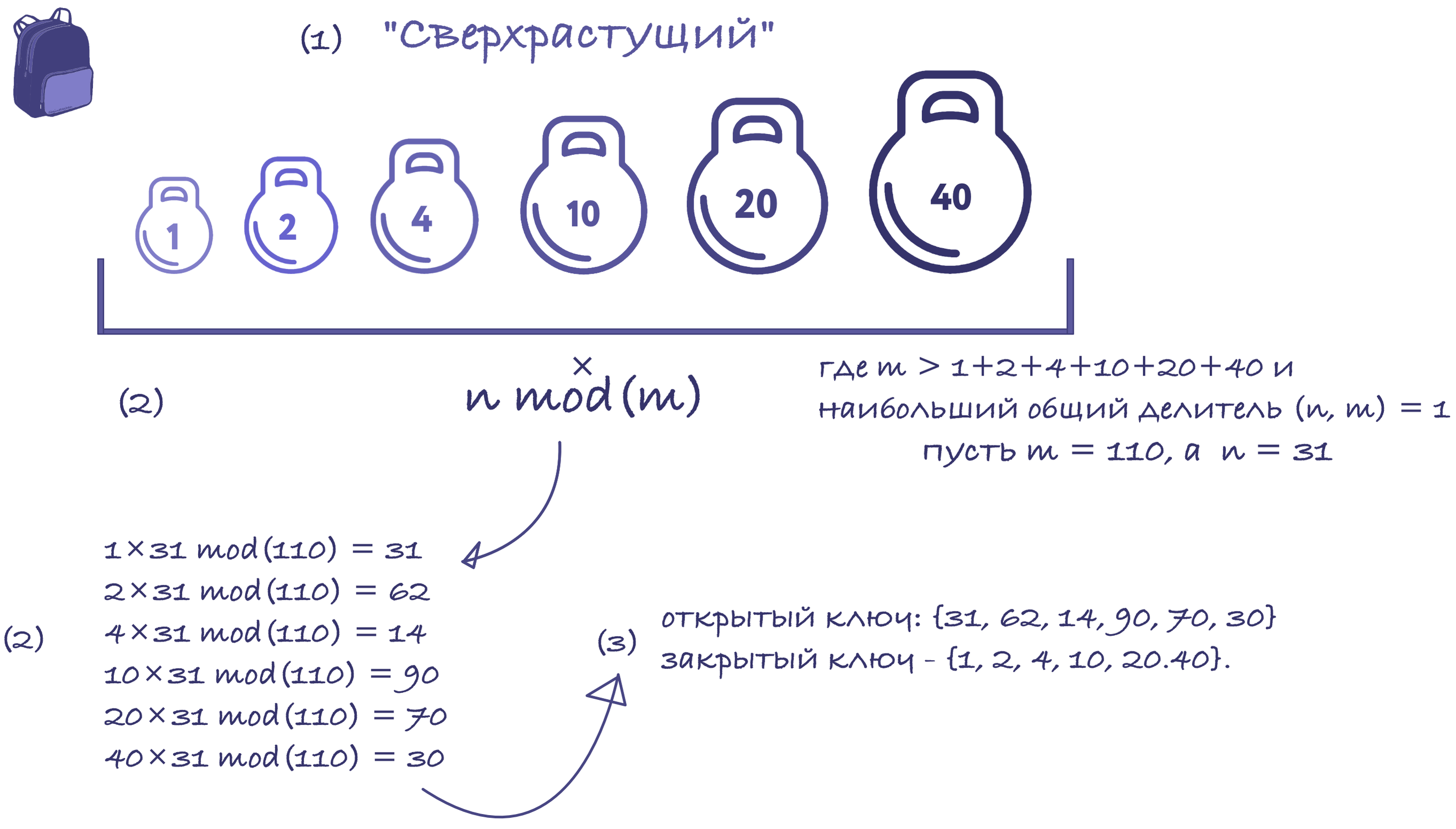
Entonces, calculamos la clave pública: {31, 62, 14, 90, 70, 30} y la clave privada: {1, 2, 4, 10, 20.40}.

Ahora intentemos enviar una secuencia binaria: 100100111100101110

Algunos de los beneficios de las claves públicas

Cuando se usa un criptosistema de clave pública, ambas partes no se encuentran, es posible que ni siquiera se conozcan y utilicen algún tipo de comunicación.

Longitud de la clave. En criptografía simétrica, si la clave es más larga que el mensaje original, no se logra una ganancia real. En cuanto a los criptosistemas de clave pública, la longitud de la clave de cifrado no importa, ya que es abierta y pública. Por lo tanto, la longitud de la clave de descifrado no es tan importante (el destinatario solo la almacena en un lugar secreto)

Historia

Durante mucho tiempo, los criptosistemas de mochila se consideraron los criptosistemas más atractivos y prometedores debido a su NP-completo y alta velocidad de cifrado y descifrado. Muchos esquemas usan el problema de la mochila (en varias variaciones), aquí hay solo algunos de ellos: el problema de la mochila compacta, el problema de la mochila multiplicativa, el problema de la mochila modular, el problema de la cubierta de la matriz, el problema de la factorización de grupos ...

Desafortunadamente, la mayoría de ellos son vulnerables a Ataques Resultó que no es trivial diseñar un criptosistema seguro basado en el problema de la mochila, aunque el problema se conoce como NP-completo. La mayoría de los criptosistemas de mochila han sido pirateados. A pesar de esto, en contraste con la factorización de enteros y el logaritmo discreto, el problema general de la mochila (solución) es un problema NP-completo probado.

Algunas personas piensan que algún día se podría inventar un algoritmo de tiempo polinomial para resolver problemas de factorización de enteros y logaritmos discretos, mientras que el problema de la mochila seguirá siendo NP completo.

Hay varios "PERO" aquí.

Primero, NP-completitud se basa en el análisis del peor de los casos, y segundo, NP-completitud son características de un problema general, no de un caso específico. Esto significa que si consideramos la complejidad media, el problema de la mochila puede ser fácil.

El material se preparó sobre la base de esta literatura:

(1) A. Salomaa. Criptografía de clave pública. - Springer-Verlag, 1990. - p. 75-82, págs.101-111

(2)Min Kin Lai. Criptosistemas de mochila : pasado y futuro - Universidad de California, 2001

(3) Baocang Wang, Qianhong Wu, Yupu Hu. Un esquema de cifrado probabilístico basado en mochila. 2007

(4) - (5)

Problema de mochila en criptografía (problema de mochila en criptografía)