epígrafe, Google / Yandex no encontró al autor
Esta es la segunda parte del artículo “Lo que está claro para todos”.
Para una mejor comprensión del algoritmo Z descrito en él, agregaré aquí un buen ejemplo dado anteriormente en la discusión / comentarios.
Imagínese que la tarea es construir una curva de alguna función T (X) en un intervalo dado de valores (permisibles). Es deseable hacer esto con el mayor detalle posible, pero no sabe de antemano cuándo será "agarrado de la mano". Desea generar los valores X para que en cualquier momento cuando se interrumpa el trazado de la curva (generando los parámetros X en el intervalo y calculando T (X)), el gráfico resultante refleje esta función con la mayor precisión posible. Tomará más tiempo, el gráfico será más preciso, pero siempre el máximo de lo que es posible en este momento para una función arbitraria .
Por supuesto, para una función conocida, el algoritmo de partición de intervalo puede tener en cuenta su comportamiento, pero aquí estamos hablando de un enfoque general que da el resultado deseado con mínimas "pérdidas". Para un caso bidimensional, puede dar un ejemplo de visualización de un cierto relieve / superficie y querer estar seguro de que, en la medida de lo posible, ha mostrado el máximo de sus características.
El problema y los objetos del modelado (de la primera parte) en el caso general pueden ser muy diferentes: hay un modelo teórico / físico o una aproximación o no (caja negra); habrá matices en la construcción de modelos en todas partes. Pero la necesidad de generar parámetros (incluido el algoritmo Z) es una parte integral y común para todos. Hay objetos (por ejemplo, tales ) cuando el tiempo para obtener T es demasiado largo (días y semanas), entonces el algoritmo para elegir un nuevo paso se detiene de acuerdo con otros criterios, no debido a la finalización del ciclo de cálculo principal en un proceso paralelo. No tiene sentido disminuir aún más el paso para mejorar la búsqueda del próximo pronóstico T si la mejora esperada es obviamente peor que el error del modelo y / o errores de medición T.
Daré una ilustración más de la división del intervalo admisible para el caso bidimensional del algoritmo Z (K = 3 en el campo 64 * 64):

Los puntos resaltados en la figura (9 uds.) Son los puntos de inicio de los bordes y la mitad del intervalo, si es necesario, se consideran fuera del algoritmo Z. Se puede ver que a lo largo de las direcciones / "caminos" horizontal y vertical que conectan estos puntos generados por el algoritmo Faltan valores Z. Los puntos adicionales aquí son fáciles de calcular por separado, pero con un aumento en el número de puntos a lo largo de estas direcciones / "pistas", la representación de la función mejorará (las "pistas" se vuelven más estrechas) y la necesidad de complementar el algoritmo en sí (se necesitan 7 líneas, de las cuales 4 operadores están en el bucle principal en n, ver más abajo) o no veo la creación de un cálculo por separado. Además, en este caso, la eficiencia media del algoritmo se deteriora y no habrá una mejora particular en la representación del modelo (incluso para n> 8, el paso en el parámetro es inferior a 1/1000, consulte la tabla siguiente).
La segunda característica del algoritmo Z es (para el caso bidimensional) la asimetría en el orden de sumar puntos: son más frecuentes en el eje / parámetro Y, la imagen se alinea al final de cada ciclo por n.
Algoritmo Z, caso unidimensional, en lenguaje VBA:
Xmax =
Xmin =
Dx = (Xmax - Xmin) / 2
L = 2
Sx = 0
For n = 1 To K
Dx = Dx / 2
D = Dx
For j = 1 To L Step 2
X = Xmin + D
Cells(5, X) = "O" ' - / T(X)
X = Xmax - D
Cells(5, X) = "O"
D = D + Sx
Next j
Sx = Dx
L = L + L
Next nAlgoritmo Z, caso 2D, lenguaje VBA:
Xmax = ' 65 - , GIF
Xmin = ' 1
Ymax = ' 65
Ymin = ' 1
Dx = (Xmax - Xmin) / 2
Dy = (Ymax - Ymin) / 2
L = 2
Sx = 0
Sy = 0
For n = 1 To K ' K = 3 GIF
Dx = Dx / 2
Dy = Dy / 2
Tx = Dx
For j = 1 To L Step 2
X1 = Xmin + Tx
X2 = Xmax - Tx
Ty = Dy
For i = 1 To L Step 2
Y = Ymin + Ty
Cells(Y, X1) = "O" ' - / T(Y,X)
Cells(Y, X2) = "O"
Y = Ymax - Ty
Cells(Y, X1) = "O"
Cells(Y, X2) = "O"
Ty = Ty + Sy
Next i
Tx = Tx + Sx
Next j
Sx = Dx
Sy = Dy
L = L + L
Next nCostos computacionales:
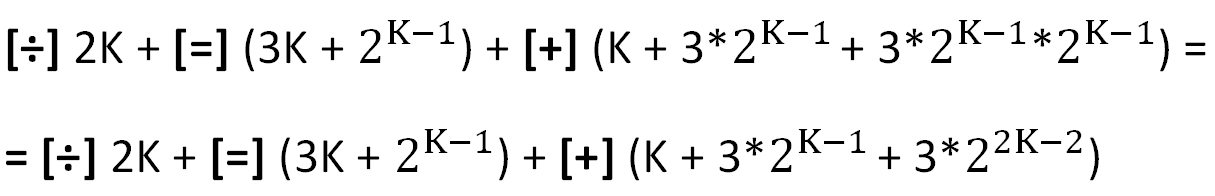
Las principales operaciones utilizadas en los cálculos se indican entre corchetes (no se tienen en cuenta los costos de organización de ciclos).
Cabe señalar aquí que la operación bastante "pesada" de la división [÷] en este caso no es cara, porque la división entera por 2 es un desplazamiento de un dígito. Los costos relativos de la operación de división y asignación ([=], segundo término) tienden rápidamente a cero a medida que K crece.
Puntos totales:

Costes medios:

Para los primeros valores de K, realizaremos cálculos utilizando estas fórmulas y completaremos la tabla:

Aquí "fracción del intervalo" es el paso relativo entre puntos al final del ciclo por n.
La última línea ("promedio") muestra el costo relativo por punto, la proporción de sumas / restas. El límite tiende a 0.5625 o 1 / 1.77777 de la operación de adición.
Volviendo a la afirmación de la primera parte del artículo , se muestra aquí que “el algoritmo propuesto para la discusión presenta costos computacionales extremadamente bajos y no presenta inconvenientes ni dificultades”, y en condiciones de interrupción repentina de los cálculos, además tiene ventajas. Es aconsejable utilizarlo en todas las aplicaciones adecuadas.
Pido ayuda para distribuir e implementar tanto software como hardware.