Roger Penrose recibió el Premio Nobel de Física 2020 "por su descubrimiento de que la formación de agujeros negros es una predicción confiable de la relatividad general".
Además, el Premio Nobel de Física fue otorgado a Reinhard Henzel y Andrea Gez "por el descubrimiento de un objeto compacto supermasivo en el centro de nuestra galaxia".
Roger Penrose es miembro de la Royal Society of London. Trabaja en diversos campos de las matemáticas, la relatividad general y la teoría cuántica. Penrose es autor de teorías relacionadas con la conciencia cuántica, el salto cuántico, la biología cuántica y el autor del libro Moda, fe, fantasía y la nueva física del universo, publicado por Peter Publishing House.
Moda, fe, fantasía y la nueva física del universo se basa en tres conferencias impartidas por Penrose en la Universidad de Princeton. El propio autor admite que normalmente la moda, la fantasía y la fe no molestan en absoluto a las personas que estudian seriamente los principios fundamentales del universo. Dejaremos la fe a las iglesias, la moda a los desfiles de moda, la fantasía a los escritores. Roger Penrose demuestra en 500 páginas que estas palabras románticas pueden ser importantes en la búsqueda de la base del universo.
Fantasía
3.1. El Big Bang y los universos de Friedman
¿Podría la fantasía desempeñar un papel no ilusorio en nuestros intentos de comprender la realidad física? Ciertamente, la fantasía es todo lo contrario de la ciencia como tal y no tiene lugar en el discurso científico serio. Sin embargo, permanece la sensación de que esta cuestión no es tan fácil de descartar como podría parecer: muchos procesos naturales parecerán fantásticos si partimos de las conclusiones a las que nos puede llevar la experiencia científica racional basada en investigaciones experimentales fiables. Como vimos, especialmente en el capítulo anterior, el mundo está realmente organizado de la manera más fantástica si lo estudiamos en el micronivel, donde reinan los fenómenos cuánticos. Un objeto material específico puede estar en varios lugares y, como un vampiro fabuloso (capaz de transformarse de murciélago en humano y viceversa cuando le plazca),puede mostrar propiedades ondulatorias o corpusculares como si lo eligiera. Además, su "comportamiento" obedece a números misteriosos, que contienen la raíz cuadrada imaginaria de -1.
Además, en una escala extremadamente grande, se están descubriendo nuevamente fenómenos, muchos de los cuales pueden parecer fantásticos, quizás incluso más sorprendentes que todos los hallazgos de la ficción literaria. Por ejemplo, a veces se observan colisiones entre galaxias enteras, y uno tiene que asumir que inevitablemente se absorben entre sí (y arreglamos esto por las distorsiones que surgen del espacio-tiempo provocadas por ambas galaxias).
De hecho, estas distorsiones del espacio-tiempo a veces se pueden observar incluso directamente, mediante la áspera curvatura de imágenes de galaxias muy distantes. Además, las distorsiones espacio-temporales más extremas que conocemos pueden conducir a la aparición de agujeros negros masivos en el espacio exterior: recientemente logramos observar cómo dos de esos agujeros se absorben entre sí y forman uno aún mayor [Abbott et al., 2016]. Hay agujeros negros que son millones o decenas de miles de millones de veces más pesados que el Sol, por lo que estos agujeros podrían tragarse fácilmente sistemas solares enteros. Sin embargo, estos monstruos son muy pequeños en comparación con las propias galaxias, en cuyos centros se encuentran. A menudo, tal agujero negro delata su existencia, generando dos haces colimados de partículas de alta energía.Estos rayos son expulsados del agujero negro en direcciones opuestas desde la diminuta región central de la galaxia en la que se encuentra el agujero; las partículas vuelan a una velocidad que puede alcanzar hasta el 99,5% de la velocidad de la luz [Tombesi et al., 2012; Piner, 2006]. Una vez pude observar cómo un rayo de este tipo salía volando de una galaxia y apuntaba a otra, como si se tratara de una colosal guerra intergaláctica.
En una escala aún mayor, regiones enteras se encuentran llenas de algo invisible que impregna el espacio. Uno tiene la impresión de que esta sustancia completamente desconocida representa aproximadamente el 84,5% de toda la materia del universo. Al mismo tiempo, hay algo más que alcanza los límites más lejanos del Universo observable y parece separarlo en diferentes direcciones con una velocidad creciente. Como si estuviera desesperado, los científicos dieron a estas dos entidades nombres bastante vagos: "materia oscura" y "energía oscura", respectivamente. Es la materia oscura y la energía oscura las que determinan principalmente la estructura general del universo conocido. El siguiente hecho parece aún más alarmante: la cosmología moderna prueba casi con certeza que todo el universo que conocemos surgió de una explosión gigante,antes del cual no había nada en absoluto, si es que podemos hablar de algo "antes" del surgimiento del continuo espacio-tiempo, que, como creemos, subyace a toda la realidad material. ¡En verdad, un concepto tan Big Bang es una idea fantástica!
Y ahí está; pero tenemos a nuestra disposición cada vez más pruebas empíricas a favor del hecho de que, en los albores de la existencia, nuestro universo era realmente increíblemente denso y se expandía rápidamente. Contenía no sólo todo el contenido material del cosmos que conocemos, sino también todo el espacio-tiempo, en cuyo contexto se desarrolla ahora la existencia de la realidad física y que, aparentemente, se extiende infinitamente en todas direcciones. Todo lo que sabemos parece haber surgido como resultado de este Big Bang. ¿Cuál es la evidencia? Debemos evaluar la credibilidad de esta idea e intentar comprender a dónde nos puede llevar.
En este capítulo discutiremos algunas ideas modernas sobre el origen del propio universo, y en particular tocaremos el siguiente problema: hasta qué punto se justifica recurrir a la fantasía para explicar hechos empíricos. En los últimos años, numerosos experimentos nos han proporcionado grandes cantidades de datos que son directamente relevantes para comprender los orígenes del universo. Cosas que antes parecían una colección de especulaciones en su mayoría no probadas se han movido a la categoría de ciencia exacta. Los más importantes son los satélites COBE, lanzado en 1989, WMAP, lanzado en 2001, y el Observatorio Espacial. Un tablón que está en funcionamiento desde 2009. Los satélites antes mencionados estudiaron gradualmente el fondo de microondas cósmico relicto (ver Sección 3.4) con más y más detalle. Sin embargo, quedan problemas sin resolver,y en busca de respuestas a ellos, algunos especialistas en cosmología teórica se adentraron en la jungla, lo que es bastante apropiado llamarla absolutamente fantástica.
Sí, hasta cierto punto, la fantasía está ciertamente justificada, pero ¿no se han apresurado los teóricos modernos con demasiado celo en esta dirección? En la sección 4.3, expresaré mi propia versión poco convencional para resolver muchos de estos misterios. Las ideas en las que está involucrada mi respuesta también pueden parecer descabelladas para algunos, y describiré brevemente por qué deben tomarse en serio. Sin embargo, en este libro estoy más interesado en los conceptos bien establecidos de las primeras etapas de la evolución de nuestro maravilloso Universo, y me gustaría discutir cuán plausibles son ciertas direcciones en las que algunos cosmólogos modernos están llevando a cabo sus investigaciones.
Para empezar, tenemos la majestuosa teoría de la relatividad general de Einstein, que se sabe que es extremadamente precisa al describir la estructura de nuestro espacio-tiempo curvo y el movimiento de los cuerpos celestes (véanse las Secciones 1.1 y 1.7). En 1922 y 1924, tras los primeros intentos de Einstein de aplicar esta teoría para describir la estructura integral del Universo, el matemático ruso Alexander Fridman encontró por primera vez soluciones para las ecuaciones de campo de Einstein en el contexto de una distribución espacialmente uniforme (homogénea e isótropa) de materia en expansión, y un líquido ideal se consideró un modelo aproximado de dicha materia. (solución de polvo) que representa la distribución media de masa-energía de las galaxias [Rindler, 2001; Wald, 1984; Hartle, 2003; Weinberg, 1972]. De hecho, desde un punto de vista empírico, pareceque en este caso se obtiene una aproximación general bastante buena a la distribución promedio de materia en el Universo existente, y se deriva el tensor de energíaT , que Friedman necesitaba para representar la gravedad en la ecuación de Einstein G = 8π ע T + Λg (consulte la Sección 1.1). Un rasgo característico de los modelos de Friedman es que la expansión comienza con una singularidad (ahora este momento se llama Big Bang). Entonces, la curvatura del espacio-tiempo era infinita, y la densidad de masa-energía de la fuente de materia T se precipitaría hasta el infinito si intentáramos rebobinar el tiempo hasta esta singularidad del espacio-tiempo.
(Sorprendentemente, el término ahora comúnmente utilizado "Big Bang" fue concebido como un peyorativo; acuñado por Fred Hoyle, un ferviente partidario de la teoría alternativa de un universo estacionario; consulte la Sección 3.2.) Primero mencionó las palabras "Big Bang" en una radio de la BBC. hecho en 1950. La sección 3.10 menciona estas entrevistas en un contexto diferente; más tarde, se compiló un libro sobre su base [Hoyle, 1950].
Si bien asumiré condicionalmente que la muy pequeña constante cosmológica de Einstein Λ, es esta constante la que determina la expansión acelerada del Universo, mencionada anteriormente (ver también la Sección 1.1), es igual a cero. Entonces necesitamos considerar solo tres situaciones separadas determinadas por la geometría espacial: la curvatura del espacio K puede ser positiva (K> 0), cero (K = 0) o negativa (K <0). En los libros autorizados sobre cosmología, se acostumbra normalizar el valor de K, llevándolo a uno de tres valores: 1, 0, –1. Aquí la historia será más clara si consideramos K como un número real que caracteriza la curvatura real del espacio. Podemos pensar en K como una cantidad que indica tal curvatura espacial en un tiempo t especialmente seleccionado. Por ejemplo, puede aceptarque t corresponderá a la época de la última dispersión (ver Sección 3.4), cuando se formó el fondo cósmico de microondas, pero la elección de un momento específico no es importante en este caso. La conclusión es que el signo de K no cambiará con el tiempo, por lo tanto, un valor positivo, negativo o cero de K caracteriza al modelo como un todo, independientemente del "punto de referencia" elegido.
Sin embargo, cabe señalar que el valor de K por sí solo no caracteriza completamente la geometría del espacio-tiempo. También existen versiones "plegadas" no estándar de dichos modelos, cuya geometría espacial es bastante compleja y, en algunos ejemplos, el Universo puede ser finito, incluso si K = 0 o K <0. Algunos científicos estaban interesados en
tales modelos (ver Levin [2012], Luminet et al., [2003], originalmente Schwarzschild [1900]). Sin embargo, estos modelos no son importantes para nosotros aquí; este problema no afecta significativamente a la mayoría de los argumentos que presento en este caso. Si no tenemos en cuenta las complicaciones topológicas, obtenemos solo tres tipos de geometría homogénea, que (en el plano) fueron muy bellamente representados por el artista holandés M.K. Escher (Fig. 3.1; compárese también con la Fig. 1.38 en la sección 1.15). La imagen 3D se ve igual.
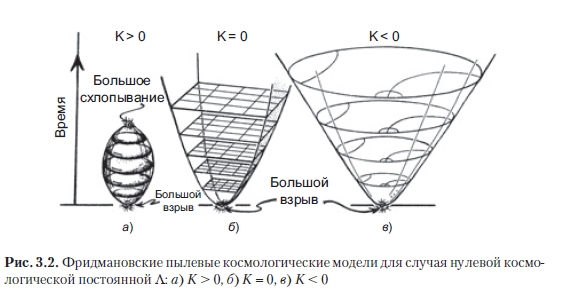
La forma más fácil de entender el caso es K = 0, ya que en este caso la sección espacial será un espacio euclidiano tridimensional ordinario, aunque para describir el Universo en expansión, necesitaremos muchas secciones sucesivas de este tipo: ver Fig. 3.2 b. (Esta expansión puede entenderse en términos de las líneas temporales divergentes que corresponden a las líneas del mundo de las galaxias idealizadas descritas por este modelo. Estas serán las líneas temporales, de las que hablaremos más adelante). Los espacios tridimensionales, que son secciones espaciales en el caso de K> 0, son un poco más difíciles de representar. ya que son 3 esferas (), cada una de las cuales en tres dimensiones es análoga a la superficie bidimensional de una esfera ordinaria (), y la expansión del Universo se expresa como un aumento en el radio de la esfera con el tiempo (figura 3.2 a). En el caso de curvatura negativa (K <0), los espacios tridimensionales tienen geometría hiperbólica (también conocida como geometría de Lobachevsky). Dicha geometría se puede representar con precisión usando la representación conforme (Beltrami - Poincaré), que en el caso bidimensional se describe como una región delimitada por un círculo S en el plano euclidiano, donde las líneas rectas se representan como arcos circulares que intersecan el círculo delimitador en ángulos rectos (Fig. 3.2 en y la Figura 1.38 en la sección 1.15) (ver, en particular, RQR, secciones 2.4–2.6; Needham [1997]). La geometría hiperbólica tridimensional se ve similar, sin embargo, en lugar de un círculo S, contiene una esfera (2 esferas ordinarias), que delimita una región (3 bolas) en el espacio tridimensional euclidiano.
El término "conforme" utilizado en estos modelos se utiliza porque en la geometría hiperbólica el ángulo entre dos curvas suaves en su punto de intersección será el mismo que en la geometría euclidiana de fondo (por ejemplo, los ángulos en las puntas de las aletas de pescado en la Fig. 1.38a o las alas de los demonios en la figura 3.1c se presentan sin distorsión, sin importar qué tan cerca del círculo delimitador estén ubicadas). Otra formulación (aproximada) del mismo principio es que las formas (pero no las dimensiones) de los detalles muy finos en tales representaciones siempre se muestran sin distorsión (ver también la Figura A.39 en la Sección A.10).
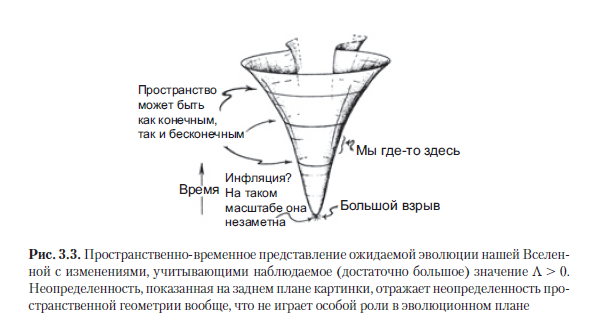
Como se señaló anteriormente, ya se ha encontrado alguna evidencia convincente de que en nuestro Universo la constante cosmológica Λ tiene un valor positivo pequeño, por lo que debemos considerar los modelos de Friedmann correspondientes a Λ> 0. De hecho, no importa cuán insignificante sea Λ, su valor sigue siendo suficiente es grande (al mismo tiempo, de acuerdo con las ecuaciones de Einstein, seguimos considerándolo una constante) para superar el colapso y el “gran colapso” que se muestra en la Fig. 3.2 a. En cambio, con los tres posibles valores de K permitidos por las observaciones actuales, el universo debería eventualmente expandirse con aceleración. Con una constante tan positiva Λ, la expansión del Universo continuará indefinidamente y eventualmente se volverá exponencial (vea la Figura A.1 en la Sección A.1).De acuerdo con tales cálculos, imaginamos la historia general del Universo como se muestra en la Fig. 3.3. El fondo se representa de manera vaga para mostrar que las observaciones permiten las tres variaciones en la curvatura espacial de K.
Las variantes del futuro lejano en todos estos modelos para Λ> 0, aunque existan algunas irregularidades en ellos, son muy similares y están bien descritas por un modelo espacio-tiempo específico, que se denomina espacio de Sitter. El tensor T de Einstein en él es simplemente Λg . Este modelo fue encontrado por Willem de Sitter (e independientemente por Tullio Levi-Civita) en 1917 (ver [de Sitter, 1917a, b; Levi-Cività, 1917; Schrödinger, 1956]; PKR, p. 28.4). En la actualidad, se acepta generalmente que este modelo se aproxima bien al futuro lejano de nuestro Universo, cuando el tensor de energía está completamente determinado por Λ, por lo tanto, en un futuro extremadamente lejano, se desarrollará la situación G≈Λg .
Por supuesto, aquí asumimos que las ecuaciones de Einstein (G = 8π ע T + Λg)actuará indefinidamente y el valor de Λ, definido en nuestro tiempo, se mantendrá constante. En la sección 3.9, se mostrará que, de acuerdo con las ideas exóticas de la cosmología inflacionaria, el modelo de De Sitter debería haber descrito el Universo en una etapa mucho más temprana, inmediatamente después del Big Bang, pero el valor de Λ en ese momento debería haber sido colosalmente más alto que el actual. Estas preguntas serán importantes para nosotros más adelante (consulte las Secciones 3.7-3.9 y 4.3), pero por ahora no nos detendremos en ellas en detalle.
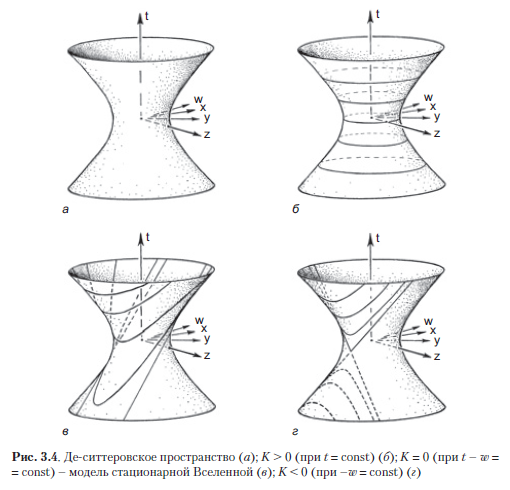
El espacio de De Sitter es un espacio-tiempo altamente simétrico que puede describirse como una (pseudo) esfera en el espacio de Minkowski de cinco dimensiones (figura 3.4 a). Esta (pseudo-) esfera surge en el punto = –3 / Λ, obteniendo la estructura métrica local del espacio de Minkowski de cinco dimensiones circundante con coordenadas (t, w, x, y, z) (Aquellos que saben cómo escribir métricas de la manera estándar usando diferenciales entienden que esta métrica de Minkowski de cinco dimensiones toma la forma =.) El espacio De-Sitter repite completamente la simetría del espacio tetradimensional de Minkowski; en ambos casos, tenemos un grupo de simetría de 10 parámetros. También puede recordar el espacio hipotético anti-des-Sitter discutido en la sección 1.15. Está muy relacionado con el espacio de Sitter y tiene un grupo de simetría del mismo orden.
El espacio de De Sitter es un modelo vacío en el que el tensor de energía Tes cero, por lo que no hay galaxias (idealizadas) que puedan definir líneas de tiempo, cuyas secciones espaciales tridimensionales ortogonales permitirían definir geometrías tridimensionales específicas de "tiempo sincrónico". De hecho, un hecho bastante notable: resulta que tales secciones espaciales tridimensionales (con tiempo sincrónico) se pueden seleccionar en el espacio de De Sitter de tres formas fundamentalmente diferentes, de modo que el espacio de De Sitter se puede interpretar como un Universo que se expande uniformemente en el espacio con cada una de las tres alternativas. tipos de curvatura espacial, dependiendo de cómo esté cortada por tales secciones tridimensionales correspondientes al mismo tiempo cósmico: K> 0 (en t = constante), K = 0 (en t - w = constante) y K <0 ( en –w = constante) (Fig. 3.4 b - d).Esto fue bellamente demostrado por Erwin Schrödinger en su libro Expanding Universes (1956). Un modelo anterior de un universo estacionario, que discutiremos en la Sección 3.2, es descrito por el espacio de De Sitter de acuerdo con la sección transversal K = 0 que se muestra en la Fig. 3.4 c (y presentado conforme a la figura 3.26 b en la sección 3.5). La mayoría de las versiones de la cosmología inflacionaria (a la que llegaremos en la sección 3.9) también utilizan ese corte K = 0, por lo que la inflación puede continuar de manera uniforme y exponencial durante un tiempo ilimitado.26 b en la Sección 3.5). La mayoría de las versiones de la cosmología inflacionaria (a la que llegaremos en la sección 3.9) también utilizan ese corte K = 0, por lo que la inflación puede continuar de manera uniforme y exponencial durante un tiempo ilimitado.26 b en la Sección 3.5). La mayoría de las versiones de la cosmología inflacionaria (a la que llegaremos en la sección 3.9) también utilizan este corte K = 0, por lo que la inflación puede continuar de manera uniforme y exponencial durante un tiempo ilimitado.
De hecho, con respecto a la estructura a gran escala de nuestro Universo real, las observaciones modernas no nos permiten responder de manera inequívoca cuál de estas variantes de geometría espacial la describe con mayor precisión. Sin embargo, cualquiera que sea la respuesta final, ahora no parece que la opción K = 0 esté tan cerca de la verdad (digno de mención, especialmente dada la evidencia aparentemente convincente a favor de K <0 que apareció hacia fines del siglo XX). En cierto sentido, esta situación es extremadamente insatisfactoria desde un punto de vista empírico; porque si solo podemos decir que el valor de K es muy cercano a cero, entonces todavía existe la posibilidad de que una observación más cuidadosa (o una teoría más convincente) muestre posteriormente queque nuestro Universo corresponde más precisamente a alguna otra geometría espacial (es decir, esférica o hiperbólica). Entonces, si al final hay buena evidencia a favor de K> 0, esto será verdaderamente importante desde un punto de vista filosófico, ya que significaría que las dimensiones espaciales del universo son finitas. Sin embargo, a partir de ahora, es costumbre decir simplemente lo siguiente: según las observaciones, K = 0. Esta puede ser una muy buena aproximación, pero en cualquier caso no sabemos qué tan cerca está el universo real de la verdadera homogeneidad espacial e isotropía, especialmente dados ciertos datos contradictorios. obtenido al observar el fondo cósmico de microondas (por ejemplo, [Starkman et al., 2012; Gurzadyan y Penrose, 2013, 2016]).si al final hay buena evidencia a favor de K> 0, esto será verdaderamente importante desde un punto de vista filosófico, ya que significaría que las dimensiones espaciales del universo son finitas. Sin embargo, a partir de ahora, es costumbre decir simplemente lo siguiente: según las observaciones, K = 0. Esta puede ser una muy buena aproximación, pero en cualquier caso, no sabemos qué tan cerca está el universo real de la verdadera homogeneidad espacial e isotropía, especialmente dados ciertos datos contradictorios. obtenido al observar el fondo cósmico de microondas (por ejemplo, [Starkman et al., 2012; Gurzadyan y Penrose, 2013, 2016]).si al final hay buena evidencia a favor de K> 0, esto será verdaderamente importante desde un punto de vista filosófico, ya que significaría que las dimensiones espaciales del universo son finitas. Sin embargo, a partir de ahora, es costumbre decir simplemente lo siguiente: según las observaciones, K = 0. Esta puede ser una muy buena aproximación, pero en cualquier caso no sabemos qué tan cerca está el universo real de la verdadera homogeneidad espacial e isotropía, especialmente dados ciertos datos contradictorios. obtenido al observar el fondo cósmico de microondas (por ejemplo, [Starkman et al., 2012; Gurzadyan y Penrose, 2013, 2016]).Sin embargo, a partir de ahora, es costumbre decir simplemente lo siguiente: según las observaciones, K = 0. Esta puede ser una muy buena aproximación, pero en cualquier caso, no sabemos qué tan cerca está el universo real de la verdadera homogeneidad espacial e isotropía, especialmente dados ciertos datos contradictorios. obtenido al observar el fondo cósmico de microondas (por ejemplo, [Starkman et al., 2012; Gurzadyan y Penrose, 2013, 2016]).Sin embargo, a partir de ahora, es costumbre decir simplemente lo siguiente: según las observaciones, K = 0. Esta puede ser una muy buena aproximación, pero en cualquier caso no sabemos qué tan cerca está el universo real de la verdadera homogeneidad espacial e isotropía, especialmente dados ciertos datos contradictorios. obtenido al observar el fondo cósmico de microondas (por ejemplo, [Starkman et al., 2012; Gurzadyan y Penrose, 2013, 2016]).
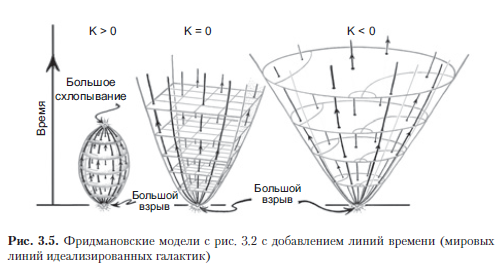
Para construir una imagen del espacio-tiempo completo de acuerdo con los modelos de Friedmann y sus generalizaciones, es necesario saber cómo cambiarán las "dimensiones" de nuestra geometría espacial con el tiempo y desde el principio. En modelos cosmológicos estándar, por ejemplo, de Friedman, o en modelos generalizados, brevemente referidos como FLRU (Friedman - Lemaitre - Robertson - Walker), en todos los modelos de esta clase general las secciones espaciales son homogéneas e isotrópicas y el espacio-tiempo total tiene la misma simetría que y las propias secciones. Tienen una definición clara del tiempo cósmico t, que describe la evolución de tal modelo universal. Este tiempo cósmico comienza en el momento t = 0 (Big Bang) y es contado por relojes idealizados que siguen las líneas del mundo de las galaxias idealizadas (Fig.3.5, así como Fig.1.17 en la sección 1.7). Me referiré a estas líneas del mundo como líneas de tiempo en el modelo FLRU (en los trabajos cosmológicos a veces también se les llama líneas del mundo de los observadores fundamentales). Las líneas de tiempo son curvas geodésicas ortogonales a las secciones espaciales que, a su vez, son 3 planos con el mismo valor t.
El caso del espacio de De Sitter tiene una característica importante: dado que, como se mencionó anteriormente, el espacio está vacío, es decir, el tensor de energía-momento T en la ecuación G = 8πT + Λg es igual a cero, entonces no tenemos ninguna línea de mundo asociada con cuerpos materiales, lo que permitió ¿Definiríamos líneas de tiempo o, respectivamente, geometría espacial? Por tanto, a nivel local tenemos la opción de cómo interpretar este modelo de descripción del Universo: si corresponde a K> 0, K = 0 o K <0. Sin embargo, globalmente, estas tres situaciones difieren, como se puede ver en la Fig. 3.4 b - d: en cada uno de estos casos, el corte captura una parte diferente del espacio integral de-Sitter. Más lejos
Partiré del hecho de que T no es igual a cero y proporciona una densidad de energía positiva de la materia, lo que hace posible determinar bien tanto las líneas de tiempo como las 3 superficies espaciales de tiempo constante para cada valor de t, como se muestra en la Fig. 3.2.
En el caso de una curvatura positiva del espacio (K> 0) en el Universo Friedman estándar lleno de polvo, su "tamaño" se puede caracterizar utilizando el radio R de secciones espaciales de 3 esferas, y este tamaño se puede estudiar en función de t. Para Λ = 0, encontramos la función R (t) que describe la cicloide en el plano (R, t) (en este caso, la velocidad de la luz se toma como una unidad: c = 1). Una cicloide es una curva con una característica geométrica simple: se describe mediante un punto de un círculo que rueda a lo largo del eje t (figura 3.6 b). Tenga en cuenta que (después del tiempo) el valor de R vuelve a llegar a cero, como en el Big Bang, por lo que todo el modelo del Universo con 0 <t < vuelve a colapsar en una singularidad, y este momento a menudo se llama un gran colapso.
En los casos restantes K <0 y K = 0 (con cero Λ), el Universo se expandirá infinitamente y no habrá un gran colapso. En el caso de K <0, hay un "radio" similar a R, pero para K = 0 uno puede simplemente elegir un par arbitrario de líneas de mundo de galaxias idealizadas y tomar como R el segmento que las divide en el espacio. En el caso de K = 0, la tasa de expansión tiende asintóticamente a cero, y en el caso de K <0, a algún valor positivo.
Las observaciones modernas indican que Λ es muy probablemente positivo y su valor es suficiente para jugar un papel decisivo en la tasa de expansión del Universo, por lo tanto, el valor de K pierde su importancia para esta dinámica, y el Universo eventualmente se descompone en una expansión acelerada, como se muestra en higo. 3.3.
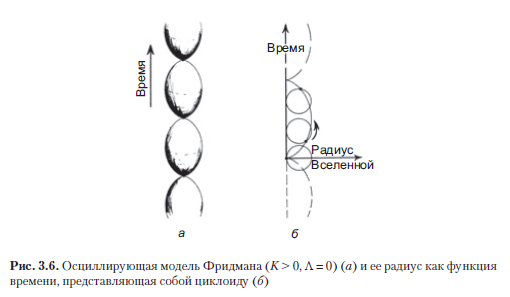
En los albores de la cosmología relativista, un modelo con un valor de K positivo (y Λ = 0) a menudo se denominaba modelo oscilante (figura 3.6 a), ya que la curva cicloide continuará indefinidamente si permitimos que el "aro" haga más de una revolución (la curva discontinua en la figura 3.6 b ). Se puede suponer que las secciones de reemplazo continuo de la cicloide pueden corresponder a ciclos sucesivos en la historia del Universo real, donde, bajo la influencia de algún tipo de sacudida, cada colapso que sufre el Universo es reemplazado por un nuevo Big Bang. Una posibilidad similar también surge en K = 0, y se puede suponer que en una etapa anterior, el espacio-tiempo sufrió un colapso, idéntico a la inversión del tiempo durante la etapa de expansión, y la Gran Implosión de esa etapa coincide con el Big Bang, que consideramos el inicio de la expansión actual del Universo.De nuevo, tendrías que imaginar algún tipo de rebote que de alguna manera te permita convertir la implosión en una extensión.
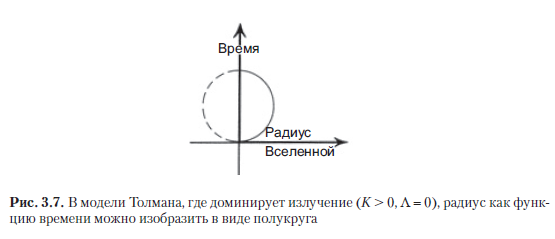
Sin embargo, para que tal imagen sea físicamente plausible, se requiere presentar algún esquema matemático convincente que esté de acuerdo con los conceptos y métodos físicos modernos y en el que encajaría tal rebote. Por ejemplo, suponga que puede cambiar las ecuaciones de estado que adoptó Friedman, con las que trató de describir la distribución general de la materia en sus galaxias "uniformemente manchadas". Friedman usó un modelo aproximado a veces llamado modelo de polvo; este modelo no tiene en cuenta ninguna interacción (excepto la gravedad) entre "elementos constituyentes" (es decir, "galaxias"), cuyas líneas de mundo son líneas de tiempo. Si cambiamos las ecuaciones de estado, esto puede afectar significativamente las propiedades de R (t) cerca de t = 0. Una aproximación aún más precisa,en lugar del polvo de Friedman (en el período inmediatamente posterior al Big Bang), aparece tal ecuación de estado, que luego fue utilizada por Richard Chase Tolman [1934], un especialista estadounidense en física matemática y cosmología. En los modelos FLRU de Tolman, se utilizó la ecuación de estado de radiación pura. Se cree que es una buena aproximación del estado de la materia en las primeras etapas del desarrollo del Universo, cuando hacía tanto calor que cada partícula tenía mucha más energía que la ecuación.que se aproxima bien al estado de la materia en las primeras etapas del desarrollo del Universo, cuando hacía tanto calor que cada partícula tenía significativamente más energía que según la ecuaciónque se aproxima bien al estado de la materia en las primeras etapas del desarrollo del Universo, cuando hacía tanto calor que cada partícula tenía significativamente más energía que según la ecuaciónpara la masa m de incluso las partículas más pesadas que podrían existir inmediatamente después del Big Bang. En el esquema de Tolman para el caso K> 0, la curva R (t) no es un arco de una cicloide, sino que (con una escala de R y t seleccionada correctamente) forma un semicírculo (figura 3.7). En el caso del modelo de polvo, se podría justificar la transición de Colapso a Explosión recurriendo a una continuación analítica (ver Sección A.10), que de hecho permite pasar de un arco de la curva cicloide al siguiente utilizando un método matemático de este tipo. Pero en el modelo de Tolman con radiación pura, la continuación analítica simplemente complementaría el semicírculo y lo convertiría en un círculo, y esto no tiene ningún sentido si este procedimiento nos interesa para describir un rebote, es decir, debe permitir una continuación hacia valores negativos de t.
Para que la nueva ecuación de estado describa el mecanismo de rebote, se necesita algo mucho más radical que la radiación de Tolman. En este caso, un punto tan serio merece atención: si se produce un rebote en alguna transición no singular, durante la cual se conservan la suavidad del espacio-tiempo y la simetría espacial del modelo, entonces las líneas de tiempo convergentes de la fase de compresión pueden convertirse en líneas de tiempo divergentes de la fase de expansión, pasando por el cuello de botella. ”Eso combinaría ambas fases. Si este cuello fuera suave (no singular), entonces la transformación de una convergencia tan extrema de líneas de tiempo en una divergencia extrema se podría lograr con una curvatura increíble del cuello, lo que conduciría a una fuerte repulsión, y esto contradice groseramente las condiciones estándar para la energía positiva.que se satisface con la materia clásica ordinaria (véanse las secciones 1.11, 3.2 y 3.7; [Hawking y Penrose, 1970]).
Por lo tanto, no se puede esperar que cualquier ecuación de estado clásica razonable nos permita describir el rebote en el contexto de los modelos FLRU, y surge inevitablemente la pregunta: ¿no nos ayudarían las ecuaciones de la mecánica cuántica a movernos en esta dirección? Es necesario tener en cuenta que cerca de la singularidad FLRU clásica, la curvatura del espacio-tiempo se vuelve indefinidamente grande. Si intentáramos describir dicha curvatura en términos de su radio, entonces este radio (el inverso de la curvatura) sería correspondientemente pequeño. Continuando con los conceptos de geometría clásica, a medida que nos acercamos a la singularidad clásica, recibiríamos radios de curvatura de espacio-tiempo cada vez más pequeños y, como resultado, el radio sería incluso menor que la escala de Planck del orden de
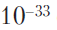ver (ver secciones 1.1 y 1.5). La mayoría de los teóricos, al pensar en la gravedad cuántica, asumen que a estas escalas, el espacio-tiempo ya sería marcadamente diferente de su forma habitual (variedad suave) (aunque en la sección 4.3 presentaré argumentos completamente diferentes a este respecto). Sea esto cierto o no, no hay razón para dudar de que los procedimientos de la relatividad general inevitablemente tendrán que ser modificados para combinarlos con los métodos de la mecánica cuántica en los enfoques de una geometría espacio-tiempo tan radicalmente curvada. Es decir, necesitamos una teoría de la gravedad cuántica adecuada para nuestro caso, que nos permita hacer frente a situaciones en las que los procedimientos clásicos de Einstein conducen a una singularidad (pero compárese con la Sección 4.3).
A menudo escuchamos declaraciones de que ese precedente ya ha sucedido. Como se señaló en la Sección 2.1, a principios del siglo XX, surgió un serio problema con los conceptos clásicos del átomo, ya que, según la teoría, los átomos deberían haber colapsado catastróficamente en un estado singular, cuando los electrones caerían en espiral sobre el núcleo (con la generación de un pulso de radiación), y resolverían este problema solo fue posible con la llegada de la mecánica cuántica. ¿No debería uno esperar que incluso cuando se habla de un colapso tan catastrófico de todo el Universo, la situación podría volverse más clara a nivel de la mecánica cuántica? Pero aquí está el truco: incluso ahora, no existe una hipótesis generalmente aceptada de la gravedad cuántica. Aún más grave es el hecho de que la mayoría de las hipótesis ya planteadas no resuelven el problema de la singularidad; las singularidades permanecen incluso en una teoría cuantificada.Hay algunas excepciones dignas de mención: la hipótesis del rebote cuántico no singular [Bojowald, 2007; Ashtekar et al., 2006], pero tendré que volver a este tema en las Secciones 3.9 y 3.11 (así como en la Sección 4.3), donde sostengo que tales hipótesis no dan muchas esperanzas para resolver el problema de la singularidad en nuestro Universo. ...
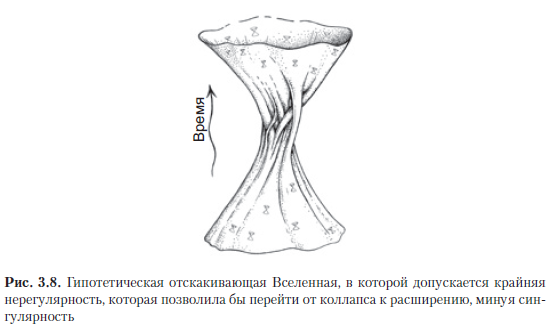
Una posibilidad completamente diferente de evitar la singularidad está asociada con la expectativa de que pequeñas desviaciones de la simetría exacta, presentes en la etapa del colapso del Universo, podrían crecer radicalmente a medida que se acerca el Gran Impacto, por lo tanto, inmediatamente antes del colapso completo, la estructura del espacio-tiempo no correspondería exactamente al modelo FLRU. Por lo tanto, a menudo se expresa la esperanza de que la singularidad que se manifiesta en los modelos FLRU pueda ser falsa y que en una situación asimétrica más general, tales singularidades clásicas del espacio-tiempo simplemente no surjan; por lo tanto, hay razones para esperar que, en el caso general, el Universo en colapso, debido a alguna geometría de espacio-tiempo intermedia compleja (Fig. 3.8), pueda convertirse en una expansión irregular.Incluso el propio Einstein trató de presentar tales argumentos: que la singularidad puede evitarse rebotando de un colapso irregular [Einstein, 1931; Einstein y Rosen, 1935] o porque el colapso final y las singularidades pueden de alguna manera prevenir los movimientos orbitales de los cuerpos celestes [Einstein, 1939].
Se puede argumentar que después de tal colapso casi singular (pero no estrictamente singular), surgirá un estado, cuyas perturbaciones se suavizarán gradualmente y, como resultado, se parecerá mucho al modelo FLRU en expansión (como en la figura 3.8). En 1963, este problema fue analizado en detalle por dos físicos teóricos soviéticos: Evgeny Mikhailovich Lifshits e Isaak Markovich Khalatnikov [Lifshits y Khalatnikov, 1963]. Su trabajo muestra que, en condiciones normales, estas singularidades aparentemente no surgen, lo que apoya la hipótesis de rebote no singular descrita anteriormente. En consecuencia, se argumentó que en la relatividad general, las singularidades espacio-temporales que surgen durante el colapso gravitacional y aparecen en las soluciones exactas conocidas de los modelos de Friedmann colapsando u otros modelos FLRU se generan solo porqueque las soluciones conocidas tienen propiedades específicas poco realistas, por ejemplo, simetría estricta. Por lo tanto, tales singularidades no se habrían desarrollado bajo las condiciones de perturbaciones asimétricas típicas. Sin embargo, este supuesto no fue confirmado, lo que se discutirá en la siguiente sección.
»Más detalles sobre el libro se pueden encontrar en el sitio web de la editorial
» Tabla de contenido
» Extracto
para los habitantes un 30% de descuento en el cupón - Penrose
Al pagar la versión impresa del libro, se envía un libro electrónico al correo electrónico.