La renormalización es posiblemente el avance más importante de la física teórica en los últimos 50 años.

No es necesario analizar el comportamiento de las moléculas de agua individuales para comprender el comportamiento de las gotas, ni analizar las gotas para comprender las ondas. La capacidad de cambiar el enfoque entre diferentes escalas es la esencia de la renormalización
En la década de 1940, los físicos pioneros tropezaron con una nueva capa de realidad. Las partículas fueron reemplazadas por campos, entidades agitadas y que lo abarcaban todo y que llenaban todo el espacio a la manera de un océano. Una pequeña ondulación en tal campo podría representar un electrón, la otra un fotón, y sus interacciones, aparentemente, podrían explicar todos los fenómenos electromagnéticos.
Solo había un problema: toda esta teoría se basaba en esperanzas y oraciones. Solo con la ayuda de una técnica como la " renormalización“Al ocultar cuidadosamente cantidades infinitas, los investigadores pudieron pasar por alto las predicciones sin sentido de la teoría. El circuito funcionó, pero incluso aquellos que desarrollaron la teoría sospecharon que podría ser un castillo de naipes que se aferra a un truco matemático retorcido.
“Yo lo llamaría un 'proceso loco'”, escribió más tarde Richard Feynman. "Tuvimos que recurrir a esos trucos, razón por la cual no pudimos demostrar que la teoría de la electrodinámica cuántica es matemáticamente consistente".
La teoría se justificó más tarde, después de varias décadas, y gracias al campo aparentemente no relacionado de la física. Los investigadores que han estudiado la magnetización han descubierto que la renormalización no se trata de infinito en absoluto. Esta teoría se refiere a la división del universo en reinos de tamaños independientes. Y esa perspectiva hoy gobierna muchos rincones de la física.
David Tong , físico teórico de la Universidad de Cambridge, escribe que la renormalización es "posiblemente el avance más importante de la física teórica en los últimos 50 años".
Historia de dos cargas
Desde algún punto de vista, las teorías de campo son las teorías científicas más exitosas. La teoría de la electrodinámica cuántica (QED), uno de los pilares del Modelo Estándar de física de partículas, ha producido predicciones teóricas que coinciden con experimentos en mil millonésimas de fracción.
Pero en las décadas de 1930 y 1940, el futuro de la teoría no era tan seguro. La aproximación del comportamiento complejo de los campos a menudo produjo respuestas infinitas y sin sentido, lo que llevó a algunos teóricos a creer que las teorías de campo son un callejón sin salida.
Feynman y otros comenzaron a buscar nuevas perspectivas, tal vez unas que devolvieran partículas a la escena, pero en cambio encontraron un truco. Descubrieron que las ecuaciones QED brindan predicciones razonables cuando se les aplica mediante un procedimiento de renormalización críptico.
El ejercicio se parece a esto. Si los cálculos de QED dan una cantidad infinita, recórtela. Convierta la parte que quiere ir al infinito en un coeficiente fijo frente a la suma. Reemplácelo con la medición final tomada en el laboratorio. Finalmente, deje que la cantidad corregida llegue al infinito.
Para algunos físicos, esta receta era como jugar en un caparazón. "Simplemente no se pueden llamar matemáticas significativas", escribió el eminente teórico cuántico Paul Dirac .
El meollo del problema, y el primer paso hacia una solución posterior, es cómo trabajan los físicos con la carga de un electrón.
En el esquema descrito, la carga eléctrica proviene de un coeficiente, un valor que se traga el infinito en el proceso de mezcla matemática. Para los teóricos, perdidos en conjeturas sobre el significado físico de la renormalización, QED insinuó que el electrón tiene dos cargas: teórica, infinita y medible, finita. Quizás la carga en el núcleo de un electrón sea infinita. Pero en la práctica, el efecto de un campo cuántico (que se puede imaginar como una nube virtual de partículas cargadas positivamente) envuelve al electrón de tal manera que los experimentadores miden solo una carga neta modesta.
Dos físicos, Murray Gell-Many Francis Lowe, formalizaron esta idea en 1954. Él acopló dos cargas de un electrón con una carga "efectiva", que varía con la distancia. Cuanto más se acerque (cuanto más se adentre en la nube de electrones positivos), más carga verá.
Su trabajo primero vinculó la renormalización a la idea de escalas. A partir de él, se podría concluir que los físicos cuánticos habían encontrado la respuesta correcta a la pregunta incorrecta. En lugar de preocuparse por los infinitos, tuvieron que lidiar con la fusión de lo pequeño con lo enorme.
La renormalización es "una versión matemática del microscopio", dijo Astrid Eichorn., un físico de la Universidad del Sur de Dinamarca que utiliza la renormalización para buscar teorías de la gravedad cuántica. “Por el contrario, puede comenzar con el sistema microscópico y alejarse. Es una combinación de microscopio y telescopio ".
Los imanes salvan el día
La segunda pista provino del mundo de la materia condensada , donde los físicos se preguntaban cómo un modelo burdo de un imán podía predecir con precisión los detalles sutiles de ciertas transformaciones. El modelo de Ising no era más que una cuadrícula de flechas atómicas, cada una de las cuales solo podía apuntar hacia arriba o hacia abajo y, sin embargo, predijo el comportamiento de los imanes reales con una precisión increíble.
A bajas temperaturas, la mayoría de los átomos se alinean, lo que magnetiza la sustancia. A altas temperaturas, se produce un desorden y la rejilla se desmagnetiza. Pero en el punto crítico de transición, hay islas de átomos alineados de varios tamaños. Lo que es importante, la distribución de ciertas cantidades en este punto crítico resulta ser la misma en el modelo de Ising, en imanes reales de diferentes materiales, en sistemas no magnéticos, como una transición a alta presión, cuando el agua se vuelve indistinguible del vapor. El descubrimiento de este llamado. la versatilidad era tan extraña como el descubrimiento de que la velocidad máxima de los elefantes y las garcetas era exactamente la misma.
Los físicos no suelen trabajar con objetos de diferentes tamaños al mismo tiempo. Sin embargo, este comportamiento universal en la vecindad del punto crítico los obligó a lidiar con longitudes de todas las escalas a la vez.
Leo Kadanov, un investigador de materia condensada, descubrió cómo lidiar con esto en 1966. Desarrolló la técnica de "dividir los giros en bloques". La celosía de Ising, demasiado compleja para trabajar directamente, se dividió en bloques de tamaño modesto, con varias flechas en cada lado. Calculó la orientación promedio del grupo de flechas y reemplazó todo el bloque con este valor. Al repetir el proceso, suavizó los detalles de la malla fina alejándose para comprender el comportamiento general del sistema.
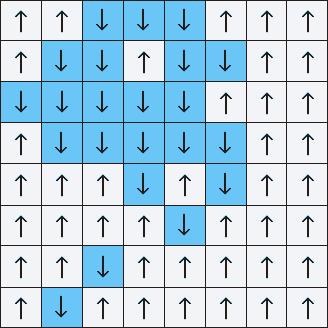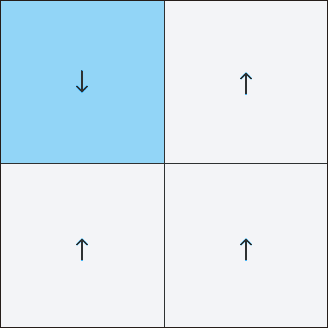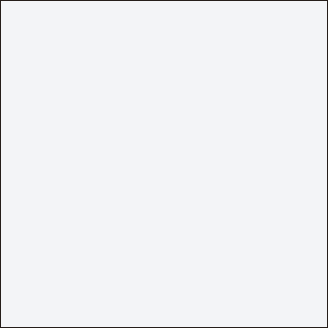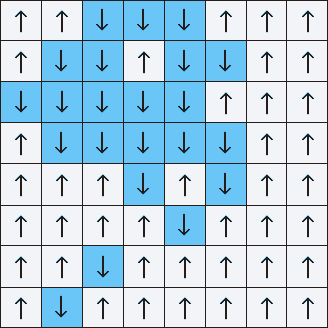
La renormalización de giro de bloque promedia una cuadrícula con muchos giros individuales, convirtiéndolos en bloques de tamaño cada vez mayor
Finalmente, Ken Wilson, un ex alumno de Gell-Man, que se dedicó inmediatamente a la física de partículas y materia condensada, combinó las ideas de Gell-Man y Lowe con las de Kadanoff. Su " grupo de renormalización ", que él describió por primera vez en 1971, justificó los cálculos pervertidos de QED y proporcionó una escalera para los sistemas universales. Este trabajo le valió un premio Nobel y cambió la física para siempre.
Paul Fendley , científico de materia condensada de la Universidad de Oxford, cree que es mejor presentar el concepto del grupo de renormalización de Wilson como una "teoría de teorías" que combina lo microscópico con lo macroscópico.
Tomemos una rejilla magnética. A nivel microscópico, es fácil escribir una ecuación que conecte dos flechas adyacentes. Sin embargo, será casi imposible extrapolar esta fórmula a billones de partículas. Estás en la escala incorrecta.
El grupo de renormalización de Wilson describe la transformación de la teoría de bloques de construcción en teoría de estructuras. Empiece con la teoría de las piezas pequeñas, digamos, los átomos de una bola de billar. Gire el mango del aparato matemático de Wilson y tendrá una teoría relacionada que describe grupos de estas piezas, por ejemplo, las moléculas de una bola de billar. Gira más, la escala disminuye y los volúmenes de los grupos crecen: aparecen grupos de moléculas, sectores de una bola de billar, etc. Como resultado, será posible calcular algo interesante, por ejemplo, la trayectoria de toda la bola.
Esta es la magia del grupo de renormalización: ayuda a determinar qué cantidades serán útiles para medir y qué detalles microscópicos complejos se pueden ignorar. Al surfista le interesa la altura de las olas, no el aplastamiento de las moléculas de agua. En física subatómica, la renormalización les dice a los físicos cuándo pueden trabajar con un protón relativamente simple en lugar de la maraña de sus quarks internos.
El grupo de renormalización de Wilson también sugirió que las desgracias de Feynman y sus contemporáneos se debieron a los intentos de comprender el electrón estando infinitamente cerca de él. “No se puede esperar que las teorías funcionen a ninguna escala de distancia, por pequeña que sea”, dijo James Fraser., filósofo de la física de la Universidad de Durham, Gran Bretaña. Los físicos ahora comprenden que truncar sumas y mezclar infinitos es la forma correcta de hacer los cálculos cuando su teoría tiene un tamaño de cuadrícula mínimo. "Cortar el exceso compensa nuestra ignorancia de lo que está sucediendo en los niveles más bajos", dijo Fraser.
En otras palabras, QED y el modelo estándar simplemente no pueden decir cuál será la carga del electrón a una distancia de cero nanómetros. Estas teorías de la física se denominan "efectivas". Funcionan mejor a distancias bien definidas. El objetivo principal de la física de altas energías es descubrir qué sucede cuando las partículas se acercan.
De grande a pequeño
Hoy en día, el "proceso loco" de Feynman se usa en física con tanta frecuencia como en álgebra, y su aplicación es responsable tanto de los mayores avances en este campo como de los desafíos actuales. Durante la renormalización, las sutilezas submicroscópicas complejas suelen desaparecer. Quizás existan, pero no afectan el panorama general. “La simplicidad es una bendición”, dijo Fendley. "Hay algo divino en esto".
Este hecho matemático describe la tendencia de la naturaleza a dividirse en mundos en gran parte independientes. Al diseñar un rascacielos, los ingenieros ignoran las moléculas de acero individuales. Los químicos analizan los enlaces moleculares sin ser conscientes de los quarks y gluones. La división de los fenómenos por dimensiones lineales, expresada numéricamente en grupos de renormalización, permitió a los científicos a lo largo de los siglos pasar gradualmente de grandes a pequeños, en lugar de atacar todas las dimensiones simultáneamente.
Sin embargo, al mismo tiempo, la hostilidad de la renormalización hacia los detalles microscópicos actúa en contra de los físicos modernos ansiosos por descubrir signos de la próxima escala del micromundo. Del principio de separación de escamas se deduce que tendrán que profundizar más para superar la tendencia de la naturaleza a ocultar pequeños detalles a gigantes curiosos como nosotros.
"La renormalización nos ayuda a simplificar la tarea", dijo Nathan Seiberg , físico teórico del Instituto de Estudios Avanzados de Princeton. “Sin embargo, también esconde lo que está sucediendo en distancias cortas. No se puede conseguir todo de inmediato ".