¡Hurra!
¡El equipo de escolares rusos ocupó el segundo lugar!
Las medallas de oro fueron ganadas por Danila Demin de Sochi (36 puntos) y Alexey Lvov de Novosibirsk (36 puntos). La plata fue tomada por Ivan Gaidai-Turlov (25), Anton Sadovnichy (29) de Moscú, Danil Sibgatullin (29) de Moscú y Kazán, y Maxim Turevsky (30) de San Petersburgo.
El ganador absoluto de la Olimpiada en la competencia individual fue un escolar de China Jinmin Li, que anotó el máximo posible de 42 puntos.
Recientemente publiqué los textos de los problemas y algunos de ellos fueron resueltos por los lectores de Habr en los comentarios.
Debajo del corte hay algunas estadísticas interesantes sobre los resultados de la Olimpiada .

¡Nuestros compañeros!
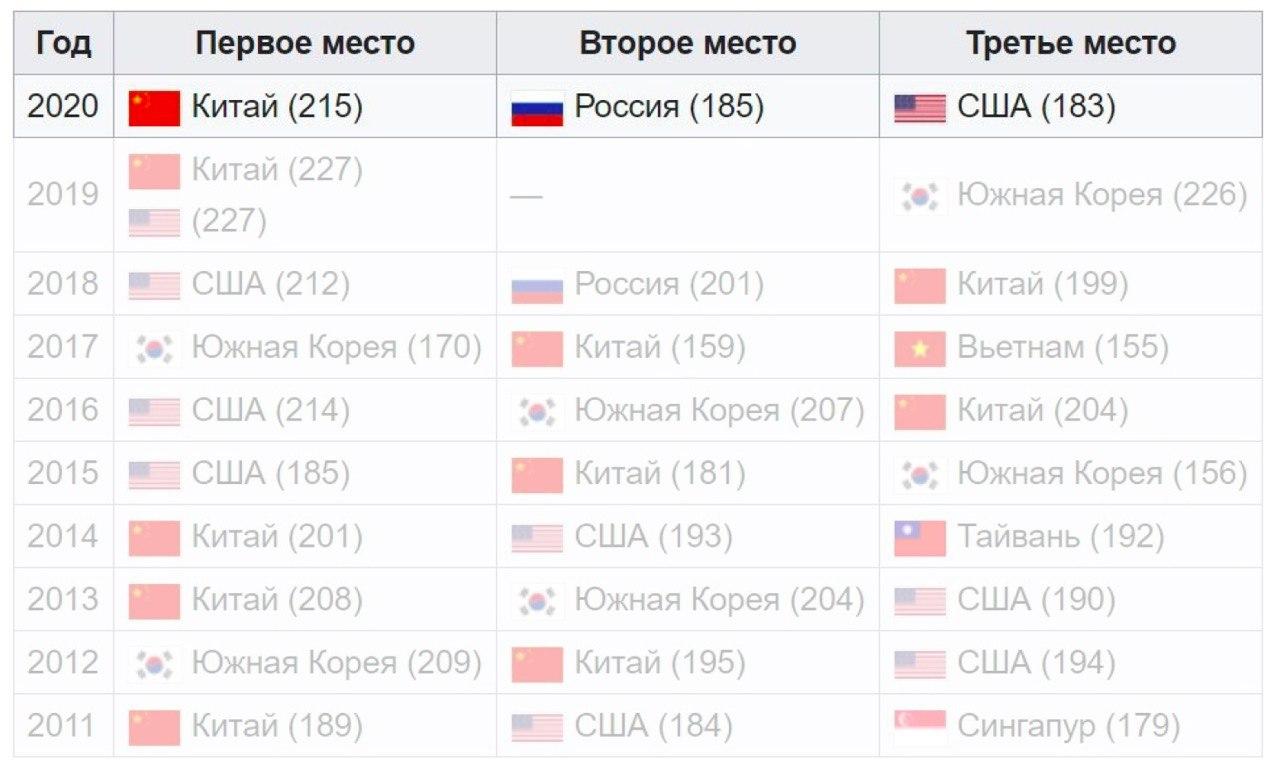
Resultados del equipo

China está liderando el camino. La brecha entre Rusia y Estados Unidos es de 2 puntos.

Es interesante que Estados Unidos tenga un líder con un apellido asiático pronunciado, y el diputado. líder - con un nombre ucraniano pronunciado y apellido.
Resultados individuales


Participantes chinos (1, 2, 3) por un amplio margen. Los representantes de muchos países obtuvieron 36 puntos (cuarto lugar).

El campeón absoluto Jinmin Li de Chongqing. El respeto.
Tareas

Problema 1
Dentro del cuadrilátero convexo ABCD, hay un punto P tal que las igualdades
∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC se mantienen.
Demuestre que las siguientes tres líneas rectas se encuentran en un punto: las bisectrices internas de los ángulos ∠ADP y ∠PCB y el punto medio perpendicular al segmento AB.
Problema 2
Dados los números reales a, b, c, d tales que a> b> c> d> 0 y a + b + c + d = 1.
Demuestre que
(a + 2b + 3c + 4d) a a b b c c d d <1.
Solución denovoselov aquí
Problema 3
Hay 4n guijarros con masas 1, 2, 3, ..., 4n . Cada uno de los guijarros está coloreado en uno de n colores, y hay 4 guijarros de cada color.
Demuestre que las piedras se pueden dividir en dos montones de igual peso total para que cada montón contenga dos piedras de cada color.
Decisión decelen aquí
Decisión denovoselov aquí
Problema 4
Se da un número entero n> 1 . Hay n 2 estaciones de funicular en la pendiente a diferentes alturas. Cada una de las dos compañías de funiculares A y B posee k ascensores. Cada ascensor realiza un traslado directo regular desde una de las estaciones a otra estación superior. Las k transferencias de la empresa A comienzan en k estaciones diferentes; también terminan en k estaciones diferentes; con una transferencia que comienza arriba y termina arriba. Se cumplen las mismas condiciones para la empresa B. Diremos que dos estaciones están conectadasempresa de funicular, si se puede llegar desde la estación inferior a la superior utilizando uno o más traslados de esta empresa (otros traslados entre estaciones están prohibidos) Encuentre el k más pequeño para el que se sabe que hay dos estaciones conectadas por ambas compañías.
Problema 5
Hay n> 1 cartas, cada una de las cuales contiene un número entero positivo.
Resultó que, para dos tarjetas cualesquiera, la media aritmética de los números escritos en ellas es igual a la media geométrica de los números escritos en las tarjetas de un determinado conjunto que consta de una o más tarjetas. ¿De qué n se sigue que todos los números escritos en las tarjetas son iguales?
Decisión denovoselov aquí
Problema 6
Demuestre que existe una constante positiva c para la cual se cumple el siguiente enunciado:
Sea S un conjunto de n> 1 puntos del plano en el que la distancia entre dos puntos cualesquiera es al menos 1. Entonces hay una línea ℓ que separa el conjunto S tal que la distancia desde cualquier los puntos S a ℓ son al menos cn −1/3 .
(La recta ℓ separa el conjunto de puntos S si corta algún segmento cuyos extremos pertenecen a S.)
Observación. Los resultados más débiles con cn −1/3 reemplazado por cn −α se pueden estimar dependiendo del valor de la constante α> 1/3 .

Estadísticas para resolver el sexto problema. Los chinos se mostraron excelentemente. El francés Vladimir Ivanov también tuvo un buen resultado.