
Hoy analizaremos el discurso de James Wootton de IBM Quantum en la conferencia FDG 2020. Hablaremos de la computación cuántica, una tecnología potencialmente prometedora, para la que, sin embargo, hay poca aplicación en la etapa actual de desarrollo. Y sin embargo, uno de ellos se encontró en generación procesal.
Hablemos con más detalle de cómo implementarlo en qubits y también proporcionemos los códigos del programa.

Comencemos con lo que son las computadoras cuánticas y cuán potencialmente útiles pueden ser. No profundicemos en los detalles técnicos. Solo mencionemos que las computadoras cuánticas son un modelo de computación completamente diferente a las computadoras digitales y analógicas. No solo aceleran el software convencional con quanta. En cambio, requieren un enfoque completamente diferente para implementar programas, así como un hardware diferente para ejecutarlos.

La computación cuántica algún día podrá realizar ciertas tareas de manera mucho más eficiente que la computación digital o analógica. Esto nos permitirá hacer frente a problemas que actualmente son imposibles de resolver. Después de décadas de investigación, se han identificado muchos algoritmos cuánticos que demuestran de manera más eficaz estas ventajas en relación con una serie de posibles aplicaciones, incluido el campo de la generación de procedimientos. Estos incluyen problemas de optimización, satisfacción de restricciones, análisis de gráficos y otros.
Construir computadoras capaces de realizar computación cuántica es una tarea desalentadora en sí misma, y se ha estado haciendo durante años. Uno de los parámetros importantes para describir un dispositivo cuántico es el número de qubits. De hecho, estos son los mismos bits, pero implementados de forma cuántica y, por lo tanto, tienen más estados que los habituales 0 y 1. En el contexto de la física cuántica, podemos escribir los valores de los bits utilizando un par de vectores ortogonales: | 0⟩ y | 1⟩. En el caso de los qubits, la descripción de los estados se complementará con amplitudes complejas c 0 y c 1 , que satisfagan la condición: | c 0 | 2 + | c 1 | 2= 1, por lo que se consigue un mayor número de estados del qubit c 0 | 0⟩ + c 1 | 1⟩.

Para ejecutar algoritmos insignia, necesitamos muchos miles de qubits, que no tendremos en los próximos años.
Actualmente, no tenemos muchos miles de qubits o incluso mil a nuestra disposición. Para ser honesto, ni siquiera tenemos cien qubits. El dispositivo más grande actualmente disponible para nosotros tiene 65 qubits. Si bien esto no es suficiente para ejecutar los algoritmos más interesantes y eficientes que conocemos, incluso esta cantidad de qubits puede proporcionar resultados que no se esperan de las computadoras convencionales. Esto se evidencia por la complejidad de emular dichos dispositivos, para lo cual deberá alquilar la supercomputadora más grande del mundo.
Entonces, el hardware cuántico puede ofrecernos respuestas únicas, pero a lo largo de las décadas no hemos aprendido a hacer las preguntas correctas. Por lo tanto, el objetivo principal de nuestra investigación actual es tratar de descubrir lo antes posible cómo hacer algo útil con estas máquinas.

También hay dispositivos de potencia más modesta, que constan de unos 20 qubits. E IBM incluso puso a disposición de forma gratuita programas cuánticos que implican hasta 15 qubits. Además, han creado un software de emulación para ayudar en el diseño y prueba de programas cuánticos. Y aunque emular más de 50 qubits es una tarea computacional abrumadora, incluso su computadora portátil puede manejar la emulación de aproximadamente 20 qubits sin ningún problema.
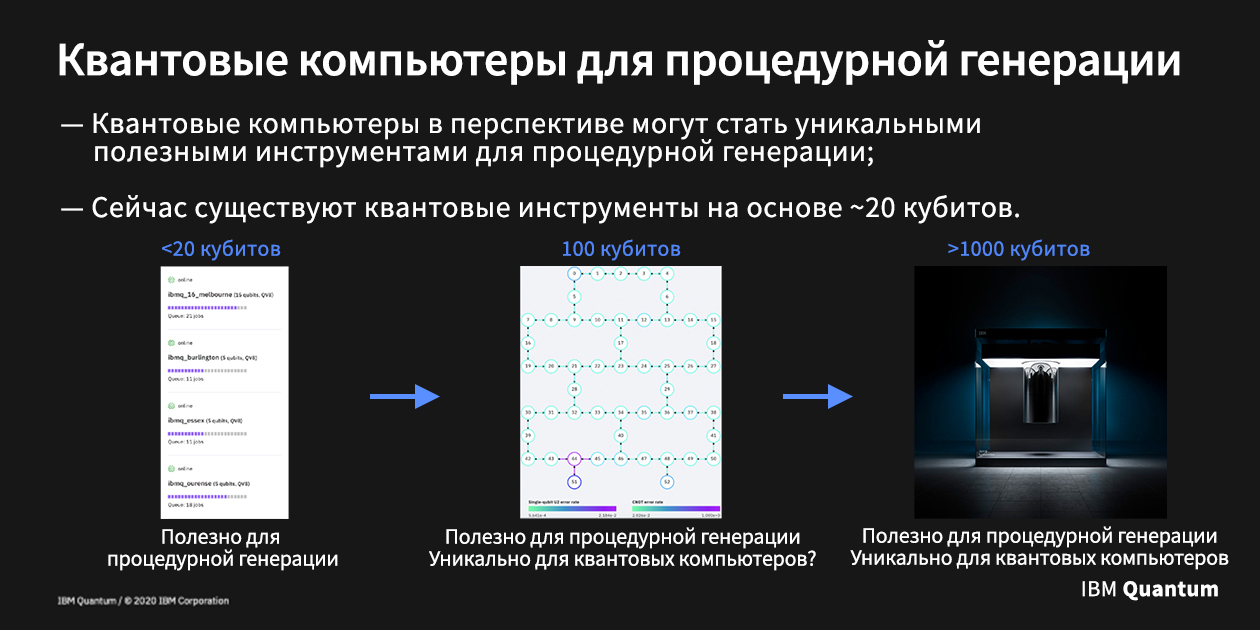
Todos los factores juntos hacen que 20 qubits sea un hito. Independientemente de si estamos utilizando hardware cuántico real o su emulación, ejecutar software cuántico de este nivel no es demasiado difícil.

Entonces, ¿qué significa todo esto para la generación de procedimientos? Depende de cuál de las tres eras esté apuntando: la de hoy, lista para proporcionar sólo decenas de qubits; para el futuro cercano, cuando los dispositivos tengan cientos de qubits; o al futuro lejano, cuando más de mil qubits estarán disponibles para nosotros.
Si hablamos de hoy, el software cuántico, centrado en el poder de solo 20 qubits, todavía no puede hacer nada único. El hecho mismo de que podamos ejecutarlo en un emulador significa que ni siquiera necesita hardware cuántico. Pero, ¿pueden los programas cuánticos hacer algo útil? ¿Podemos escribir un programa cuántico de 20 qubit que produzca resultados que sean útiles para el usuario final real?
Si podemos lograr resultados realmente útiles con 20 qubits, este efecto solo se multiplicará con el tiempo y más potencia de cálculo. La era intermedia será la era de la investigación de métodos cada vez más complejos de computación cuántica, incluido el efectivo para la generación de procedimientos. Vamos a pasar a crear herramientas en las que probablemente no hubiéramos pensado si no hubiéramos pensado en términos de cuantos.
Pero no nos adelantemos. El primer paso hacia la era de la expansión de la utilidad es demostrar que incluso el software cuántico de 20 qubits puede ser útil. Eso es lo que haremos.
Ahora toca aclarar algunos detalles.
La generación procedimental significa que necesitamos generar algo. ¿Pero que?
La generación de terreno es la más obvia, así que comencemos con eso.
El ruido Perlin es una herramienta omnipresente para la generación de terrenos procedimentales. Pero hay otro método mucho menos complicado de crearlo: usar un conjunto de puntos aleatorios con su posterior desenfoque. La implementación de algo como esto nos pareció un objetivo más alcanzable para el primer paso, por lo que lo tomaremos como base.
Comencemos por desarrollar una forma de codificar mapas de altura en forma de circuitos cuánticos, que son elementos fundamentales del software cuántico. Tienen cierta semejanza con los modelos de circuitos booleanos para la computación digital. Los Qubits son esencialmente los mismos bits que sufren diferentes cambios a medida que se realizan los cálculos.

Trabajaremos con imágenes en blanco y negro, donde el brillo de los píxeles puede tener un valor de 0 a 1. De igual forma, se pueden confundir con mapas de altura. Una vez que aprendamos a codificar estos mapas de altura como esquemas, podremos gestionarlos. La codificación utilizada tiene como objetivo comprimir tantos puntos como sea posible en el menor número de qubits posible. Este método no deja mucha flexibilidad para proporcionar un control conveniente y flexible. Al mismo tiempo, casi cualquier cambio en el circuito provocará efectos de interferencia.
Utilizamos principalmente operaciones que pueden verse como formas parciales de la puerta NOT. NO cambia el valor de 0 a 1 y viceversa para bits normales. Con las puertas cuánticas, podemos parametrizar este elemento para realizar una operación que puede hacer la mitad de NOT, o un cuarto, o cualquier otra parte fraccionaria que pueda ser representada por un conjunto de 2 n amplitudes de n qubits.
La siguiente función convierte la imagen original en un circuito cuántico:
def height2circuit(height):
#
L = max(max(height))+1
#
grid = make_grid(L)
#
n = 2*int(np.ceil(np.log(L)/np.log(2)))
#
state = [0]*(2**n)
#
H = 0
for bit string in grid:
(x,y) = grid[bit string]
if (x,y) in height:
h = height[x,y]
state[ int(bit string,2) ] = np.sqrt( h )
H += h
#
for j,amp in enumerate(state):
state[ j ] = amp/np.sqrt(H)
#
qc = QuantumCircuit(n,n)
qc.initialize(state,range(n))
# Qiskit
# qc.initialize( state, qc.qregs[0])
return qcLuego tenemos que hacer el proceso opuesto: transformar el circuito cuántico en una imagen:
def circuit2height(qc):
#
n = qc.num_qubits
grid = make_grid(int(2**(n/2)))
#
ket = qi.Statevector(qc.data[0][0].params)
qc.data.pop(0)
#
ket = ket.evolve(qc)
#
p = ket.probabilities_dict()
#
max_h = max( p.values() )
#
height = {}
for bit string in p:
if bit string in grid:
height[grid[bit string]] = p[bit string]/max_h
return heightSi aplicamos esta operación a todos los qubits, podemos ver cómo cambia el mapa de altura a medida que aumenta la fracción. Obtendrá algo así como un efecto de desenfoque. Entonces ocurrirán efectos de interferencia, creando un patrón que no se puede lograr con un simple desenfoque.
En el ejemplo anterior en (a), comenzamos con un par de puntos aparentemente arbitrarios. Poco a poco, se vuelven borrosos, tras lo cual se superponen efectos de interferencia. Esto conduce a la aparición de un patrón, en nuestro caso, como un tablero de ajedrez en (f). Este resultado en particular tiene una conexión clara con los dos píxeles con los que comenzamos. Si tomamos otros datos como punto de partida, el resultado también será completamente diferente.
Quantum Blur se ha desarrollado y probado en varios juegos. Se utiliza principalmente para generar texturas y mapas de nivel.

Después de generar estos mapas, los usamos para el análogo cuántico del ruido de alta frecuencia de Perlin.
Así que ahora creamos el perfil principal, por ejemplo, islas, de alguna otra manera, como en © en nuestro ejemplo. Entonces necesitamos un conjunto inicial de píxeles como en (a). Lo difuminamos cuánticamente para generar un patrón como (b). Después de eso, lo aplicamos al perfil principal para crear el paisaje final.
Puede ver un ejemplo 2D aquí, así como una representación 3D que se utilizó en el juego tutorial IBM QiskitBlocks. Los detalles como la información sobre el tipo de césped y la ubicación de los árboles en la representación 3D también se han desarrollado utilizando operaciones cuánticas.

Dado que las imágenes RGB son típicamente tres mapas de elevación alineados, también podemos manipular estas imágenes. De esta manera, es fácil crear algunas imágenes extrañas usando superposición. Más difícil, pero más eficaz: codificar un par de imágenes y crear un efecto de teletransportación entre ellas.
La teletransportación cuántica transfiere información entre qubits. Entonces tomamos dos registros de qubit del mismo tamaño y simplemente cambiamos sus estados. Usemos esta operación para crear una animación de transición.

También se puede utilizar una idea de codificación similar para otras formas de datos. Wootton intentó usarlo en música:
y el nivel de Mario:
Aquí hay dos ejemplos más que son importantes para nosotros. Uno de ellos es un estudio de juegos que utiliza este método para la generación de procedimientos en un juego futuro. El proyecto tiene un entorno de ciencia ficción, y el método cuántico le da un sabor genuino de ciencia.
Además, la artista Libby Heaney utilizó algunas de estas ideas como punto de partida para su trabajo.
La naturaleza cuántica de la computación se destaca en ambos casos: es importante para el usuario que los resultados provengan del dominio cuántico del espacio del algoritmo y no solo del álgebra lineal brillante.
El método descrito aquí es más adecuado para la emulación que para el hardware cuántico real, pero esto cambiará pronto. De hecho, uno de los dispositivos cuánticos más grandes de IBM también se ha utilizado para la generación de procedimientos, aunque de una manera completamente diferente.
Mientras tanto, puede probar el efecto de desenfoque cuántico usted mismo. Está escrito en Python , pero también hay un complemento para Unity . Quizás te sean útiles.
Enlace al artículo completo: aquí .