Teoría de categorías para programadores. En los dedos

Hola colegas.







Desarrollando nuestro incansable interés por la literatura académica seria , podría decirse, llegamos a la teoría de categorías . Este tema, en la famosa presentación de Bartosz Milevsky, ya apareció en Habré y ahora puede presumir de tales indicadores: es aún más agradable que logramos encontrar material relativamente nuevo (enero de 2020), que sirve como una excelente y al mismo tiempo lo más breve posible introducción a la teoría de categorías. Esperamos poder interesarle en este tema.











Si usted y yo, querido lector, enfrentamos problemas similares, entonces una vez se sintió atormentado por la pregunta "¿qué diablos es una mónada?" Luego buscaste en Google esta pregunta, deslizándote sigilosamente por la madriguera del conejo de las matemáticas abstractas , enredándote en functors , monoides , categoríashasta que se dieron cuenta de que ya se habían olvidado de la pregunta que los trajo aquí. Esta experiencia puede ser bastante abrumadora si nunca antes ha visto lenguajes de programación funcionales, ¡pero no se preocupe! He estudiado muchas páginas de densas matemáticas para usted y he visto horas de conferencias sobre este tema. Entonces, para evitarle esa necesidad, resumiré el tema aquí y también le mostraré cómo puede aplicar la teoría de categorías para que pueda pensar (y escribir código) en un estilo funcional en este momento.



Este artículo está dirigido a cualquier persona que se considere un "novato" en el campo de la programación funcional y recién esté comenzando con Scala, Haskell u otro lenguaje similar. Después de leer este artículo, se sentirá un poco más seguro al interpretar los fundamentos de la teoría de categorías e identificar sus principios "sobre el terreno". Además, si alguna vez ha probado las matemáticas teóricas, absténgase de mencionar directamente los conceptos que se tratan aquí. Como regla general, se puede decir mucho más sobre cada uno de ellos de lo que se escribe aquí, pero este artículo será suficiente para un programador curioso.

Los basicos

Entonces, ¿qué es exactamente una categoría y cómo se relaciona con la programación? Como muchos conceptos usados ​​en programación, una categoría es algo muy simple con un nombre elegante. Este es solo un gráfico dirigido etiquetado con algunas restricciones adicionales. Cada uno de los nodos de una categoría se denomina "objeto" y cada uno de sus bordes se denomina "morfismo".







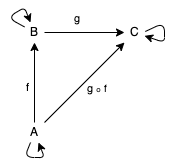
Como habrá adivinado, no todos los gráficos dirigidos son una categoría; Para que un gráfico se considere una categoría, se deben cumplir algunos criterios adicionales. En la siguiente imagen, notamos que cada objeto tiene un morfismo que apunta a sí mismo. Este es el morfismo idéntico, y cada objeto debe tener tal que el gráfico se considere una categoría. A continuación, observe que el objeto Atiene un morfismo que findicaB, y, asimismo, el objeto Btiene un morfismo que gapunta C. Dado que existe un camino desde Aa By desde Bque C, obviamente, hay un camino de Aa C, ¿verdad? Este es el siguiente requisito para las categorías de morfismos, necesariamente se debe realizar una composición asociativa, de modo que para un morfismo f: A = > B , y g: B = > Chay un morfismo h = g(f): A = > C.



Estos cálculos pueden parecer ya un poco abstractos, así que veamos un ejemplo que satisface esta definición y está escrito en Scala.

trait Rock
trait Sand
trait Glass
def crush(rock: Rock): Sand
def heat(sand: Sand): Glass

Creo que este ejemplo facilita un poco la relación. Borrar piedras en arena es un morfismo que transforma un objeto rocken un objeto sand, mientras que fundir vidrio de arena es un morfismo que transforma un objeto sanden un objeto glass. En este caso, la composición de estas relaciones definitivamente se verá como

val glass: Glass = heat(crush(rock))

También existen funciones de identidad (definidas en PredefScala), ya que para cualquier objeto no es difícil escribir una función que devuelva el mismo objeto. Por lo tanto, este sistema es una categoría, aunque bastante simple.

Mayor familiaridad con las categorías

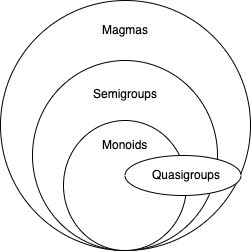
Ahora profundizaremos un poco más en la terminología de la teoría de categorías y comenzaremos con una categoría llamada magma. Si aún no está muy familiarizado con este concepto básico, permítame explicarle que el magma es solo una operación binaria, es decir, una operación sobre dos valores, como resultado de lo cual se obtiene un nuevo valor. Para no entrar en detalles, no daré aquí una prueba de que el conjunto de todas las operaciones binarias es de hecho una categoría, pero para aquellos que estén interesados ​​en los detalles, recomiendo leer el siguiente artículo de Bartosz Milevsky. Toda la aritmética desde la suma hasta la multiplicación pertenece a subcategorías, unidas por la categoría magmática (ver diagrama).



Aquí se aplica el siguiente orden de herencia:

• 1. Magma: todas las operaciones binarias
• 2. Semigroups: todas las operaciones binarias que son asociativas
• o : .
• 3. : ,
• o : , (aka )

Entonces, volviendo a nuestro ejemplo anterior, tanto la suma como la multiplicación son monoides porque son asociativas (a + (b + c) = (a + b) + c)y tienen un solo elemento (ax 1 = 1 xa = a). El último círculo de este diagrama contiene cuasigrupos para los que se pueden aplicar principios de inclusión diferentes que para los semigrupos o monoides. Los cuasigrupos son operaciones binarias que son reversibles. No es tan fácil explicar esta propiedad, por eso les remito a la serie de artículos de Mark Siman dedicados a este tema. Una operación binaria es reversible cuando para cualquier valor ay bexisten tales valores xy yque permiten convertir aab... Sé que suena complicado. Para que quede claro, veamos el siguiente ejemplo de resta:

val x = a - b
val y = a + b
assert(a - x == b)
assert(y - a == b)

Tenga en cuenta: yno participa en la resta como tal, pero el ejemplo aún cuenta. Los objetos de una categoría se abstraen y pueden ser casi cualquier cosa; en este caso, es importante que para cualquiera ay bque se pueda generar, estas declaraciones sigan siendo verdaderas.

Tipos en contexto

Independientemente de su disciplina en particular, el tema de los tipos debe quedar claro para cualquiera que entienda el significado de los tipos de datos en la programación. El entero, el booleano, el punto flotante, etc. son todos tipos, pero ¿cómo describiría el tipo platónico ideal con palabras? En su libro Teoría de categorías para programadores, que se convirtió en una serie de publicaciones de blog, Milevsky describe los tipos simplemente como "conjuntos de valores". Por ejemplo, un booleano es un conjunto finito que contiene los valores "verdadero" y "falso" (falso). Un char es un conjunto finito de todos los caracteres de letras y números, y una cadena es un conjunto infinito de caracteres.



El problema es que en la teoría de categorías tendemos a alejarnos de los conjuntos y pensar en términos de objetos y morfismos. Pero el hecho de que los tipos sean simplemente conjuntos es inevitable. Afortunadamente, hay un lugar en la teoría de categorías para estos conjuntos, ya que nuestros objetos son abstracciones y pueden representar cualquier cosa. Por lo tanto, tenemos todo el derecho a decir que nuestros objetos son conjuntos, y además consideramos nuestros programas Scala como categorías, donde los tipos son objetos y las funciones son morfismos. Esto puede parecer dolorosamente obvio para muchos; después de todo, en Scala estamos acostumbrados a tratar con objetos, pero vale la pena señalarlo explícitamente.



Si ha trabajado con un lenguaje orientado a objetos como Java, probablemente esté familiarizado con el concepto de tipos genéricos. Estas son cosas comoLinkedListo, en el caso de Scala, Option[T]donde Trepresenta el tipo de datos subyacente almacenado en alguna estructura. ¿Qué pasaría si quisiéramos crear un mapeo de un tipo a otro para que se conserve la estructura del primer tipo? Bienvenido al mundo de los functores, definido como mapeos entre categorías para mantener la estructura. En programación, normalmente tiene que trabajar con una subcategoría de functores, los denominados endofunctores, que ayudan a mapear una categoría a sí misma. Así que solo diré que cuando hablo de functores me refiero a endofunctores.



Como ejemplo de un funtor, veamos el tipo Scala Option[T]junto con nuestro ejemplo anterior, que mencionaba piedra, arena y vidrio:

val rockOpt: Option[Rock] = Some(rock)

Arriba tenemos el tipo Rockcomo lo definimos anteriormente, pero envuelto Option. Este es un tipo genérico (y más, más sobre esto a continuación), que nos dice que un objeto es una entidad específica que estamos buscando o Noneque se puede comparar con nullotros idiomas.



Si no usamos palabras funcionales, entonces podríamos imaginar cómo estamos aplicando una función crush()a Rock, lo que requeriría recurrir a un operador if para manejar la situación en la que Optiones None.

var sandOpt: Option[Sand] = None
if(rockOpt != None) {
  sandOpt = Some(crush(rockOpt.get))
}

Podríamos decir que esto es un aparte, pero por favor no use var; dicho código es malo en Scala por varias razones. Nuevamente, volviendo al tema: en Java o C # esto no sería un problema. Verifica si su valor es del tipo que esperaba ver y haga lo que quiera con él. Pero con el poder de los functors, todo se puede hacer con un poco más de elegancia con la función map():

val sandOpt: Option[Sand] = rockOpt.map(crush)

Boom, una línea y listo. Sería posible poner el primer ejemplo en una línea, usando el operador ternario o algo similar, pero no lo habría logrado de manera tan sucinta. Este ejemplo es realmente maravilloso por su simplicidad. Esto es lo que está sucediendo aquí: map()toma una función y mapea esa función (en un sentido matemático) a sí misma. La estructura se Optionconserva, pero ahora contiene Sando None, en lugar de Rocko None. Esto se puede ilustrar de esta manera:







Observe cuán maravillosamente se alinea todo, cada objeto y morfismo se conservan en ambos sistemas. En consecuencia, el morfismo en el centro es un funtor que representa un mapeo de Ta Option[T].

Juntos

Ahora finalmente podemos volver a la pregunta original "¿qué diablos es una mónada"? Hay una respuesta con la que puedes tropezar a ciegas si solo intentas buscarla en Google, y suena así: una mónada es solo un monoide en la categoría de endofunctores, que a menudo es seguido por un comentario muy sarcástico, "¿cuál es el problema?" Como regla general, de esta manera intentan mostrar en broma lo difícil que es todo en este tema, pero de hecho, no todo es tan aterrador; después de todo, ya hemos descubierto lo que significa esta frase. Vayamos paso a paso nuevamente.



Primero, sabemos que los monoides son operaciones binarias asociativas, cada una de las cuales contiene un elemento neutro (único). En segundo lugar, sabemos que los endofunctores le permiten mapear una categoría a sí misma, mientras se mantiene la estructura. Entonces, una mónada es solo una especie de tipo contenedor (como en el ejemplo de tipo genérico anterior) que mantiene algún método para aceptar una función y mapearla a sí misma. List- esta es una mónada, Option(como la que consideramos anteriormente) es una mónada, y alguien puede incluso decirte eso y Futuretambién es una mónada. Ejemplo:

val l: List[Int] = List(1, 2, 3)
def f(i: Int) = List(i, i*2, i*3)
println(l.flatMap(f)) // : List(1, 2, 3, 2, 4, 6, 3, 6, 9)

Engañosamente simple, ¿no? Como mínimo, debería haber la sensación de que no es difícil comprender todo aquí, incluso si a primera vista no está del todo claro cuál es el uso de tal concepto.