
Eliminar nodos de un árbol rojo-negro no es una tarea fácil, por lo que tiene sentido dividirlo en varias partes y considerar cada caso por separado.
cartoonbank.ru
En el último artículo, examinamos las reglas para formar un árbol de búsqueda rojo-negro y consideramos los casos de equilibrio al agregar elementos.
Ahora hablemos de eliminar elementos.
Tomemos, por ejemplo, este árbol rojo-negro:
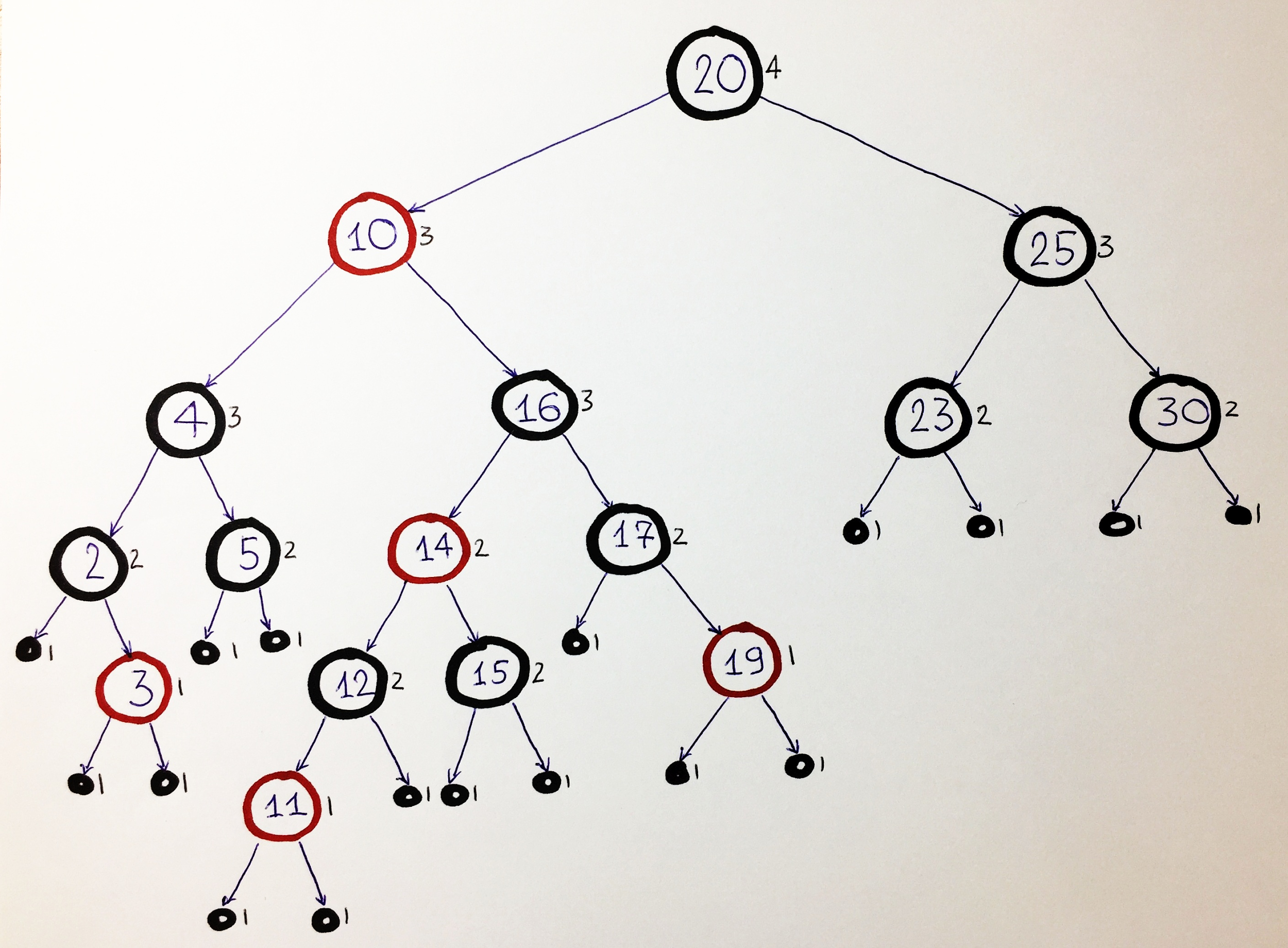
Recuerde que la propiedad principal de un árbol rojo-negro es la misma altura negra a la izquierda y a la derecha de cada nodo. Por tanto, en las figuras, junto a cada nodo, indicaremos el valor de la altura del negro, para que en cada etapa podamos comprobar su estabilidad.
Divide y vencerás
Eliminar un elemento de un árbol rojo-negro no es una tarea tan fácil como podría parecer a primera vista, por lo que propongo dividirlo en varias partes y considerar cada una por separado.
Primero, dividamos la tarea en dos categorías:
- color del nodo eliminado: K o H
- número de nodos secundarios: 2, 1 o 0
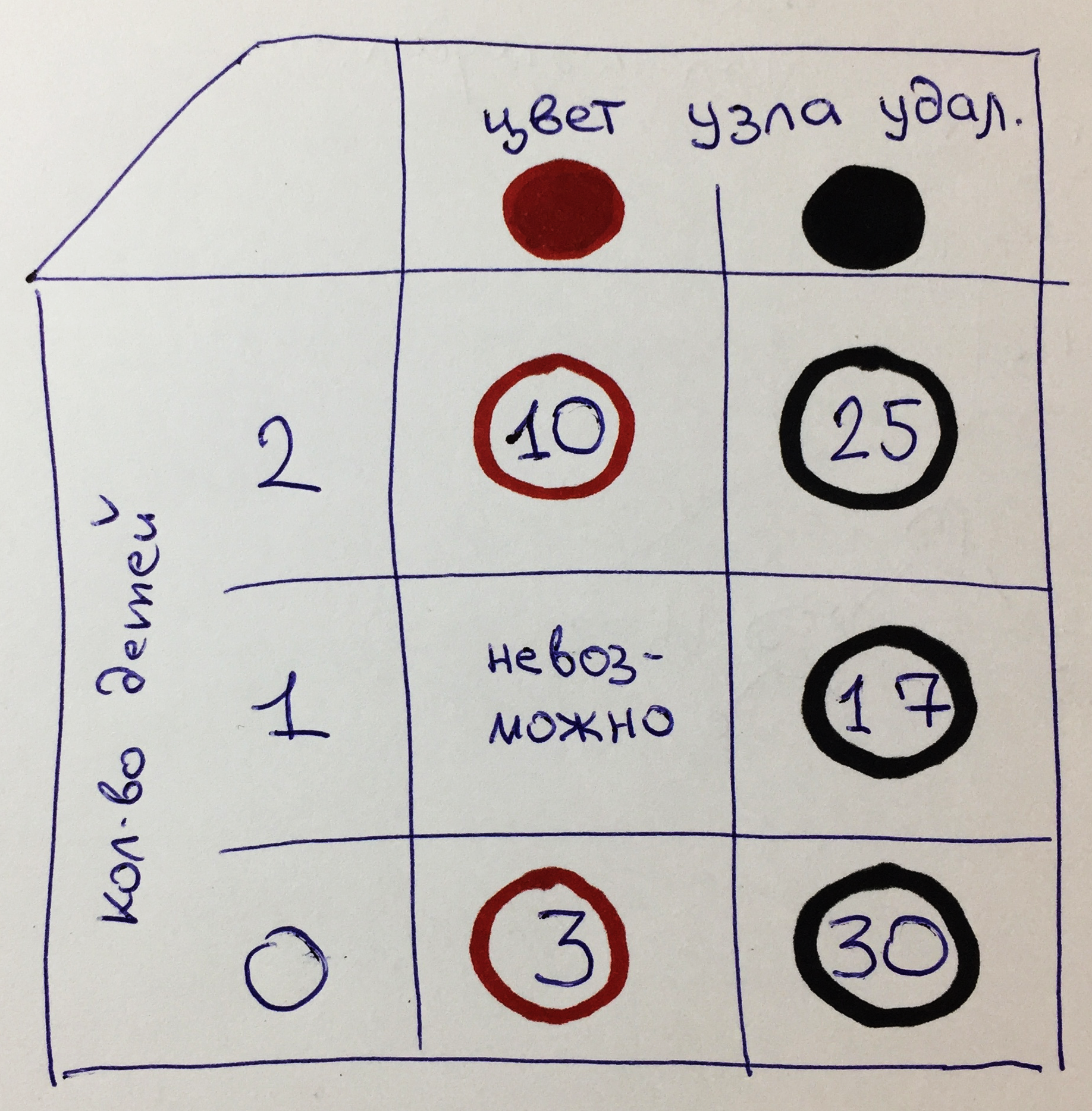
Como resultado, obtenemos una matriz de 6 opciones: K2, Ch2, K1, Ch1, K0, Ch0.
Para cada opción se indica el nodo correspondiente de nuestro árbol.
Consideremos el proceso de eliminación para cada opción.
K2 - nudo rojo con dos hijos
La tarea de eliminar un nodo con dos hijos se reduce a la tarea de eliminar un nodo con uno o cero hijos.
Para hacer esto, necesita encontrar el elemento más cercano que sea menor o mayor que el eliminado e intercambiarlos.

Tenga en cuenta que al intercambiar elementos, solo necesita cambiar los valores en los nodos y dejar el mismo color, para no romper la estructura del árbol y no cambiar la altura del negro.
Después del intercambio, debe eliminar el artículo de su nueva ubicación. Será el elemento más a la derecha en la rama izquierda (máximo a la izquierda), o el más a la izquierda a la derecha (mínimo a la derecha), en cualquier caso no tendrá un hijo a la izquierda oa la derecha. Así, la tarea de eliminar un nodo con 2 hijos se reduce a la tarea de eliminar un elemento con 1 o 0 hijos:
- K2 => K1 o K0
Ch2 - nudo negro con dos hijos
De manera similar al caso anterior, daremos un ejemplo de eliminación del nodo negro 16.

Como puede ver, después del intercambio, la tarea se reduce a eliminar un elemento con un hijo:
- Ch2 => Ch1 o Ch0
K1 - nudo rojo con un niño
Si el nodo rojo no tiene un hijo, entonces hay un elemento NIL negro en su lugar y la altura negra del nodo rojo es 1. Por lo tanto, por otro lado, la altura negra también debe ser 1. Pero dado que el nodo rojo no puede tener un hijo rojo colores, entonces su otro hijo debería ser negro. Dado que la altura del negro debe ser 1, solo puede ser un elemento NIL negro, ya que en el caso de un elemento negro normal, la altura será mayor.
Por tanto, el caso K1 no tiene lugar.
Ch1 - nudo negro con un niño
Si el elemento negro no tiene un hijo, entonces hay un elemento NIL negro con una altura negra 1. Por lo tanto, en el otro lado debería haber un nodo rojo sin hijos. Para eliminar dicho elemento, basta con transferir el valor del elemento rojo al nodo negro, mientras que se conservará la altura del negro.
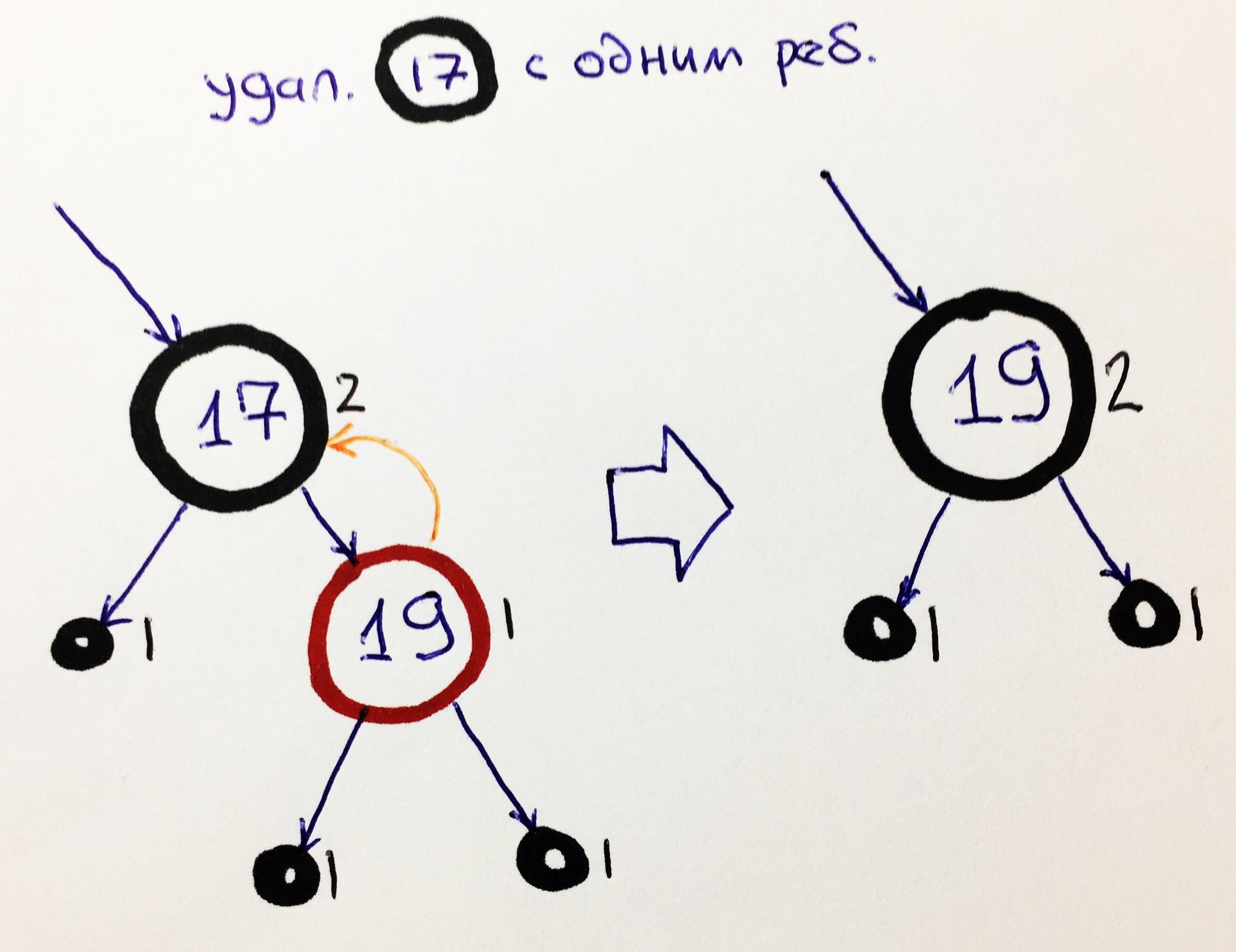
K0 - nudo rojo sin niños
El caso más simple. Simplemente eliminamos el elemento, reemplazándolo con una referencia NIL:
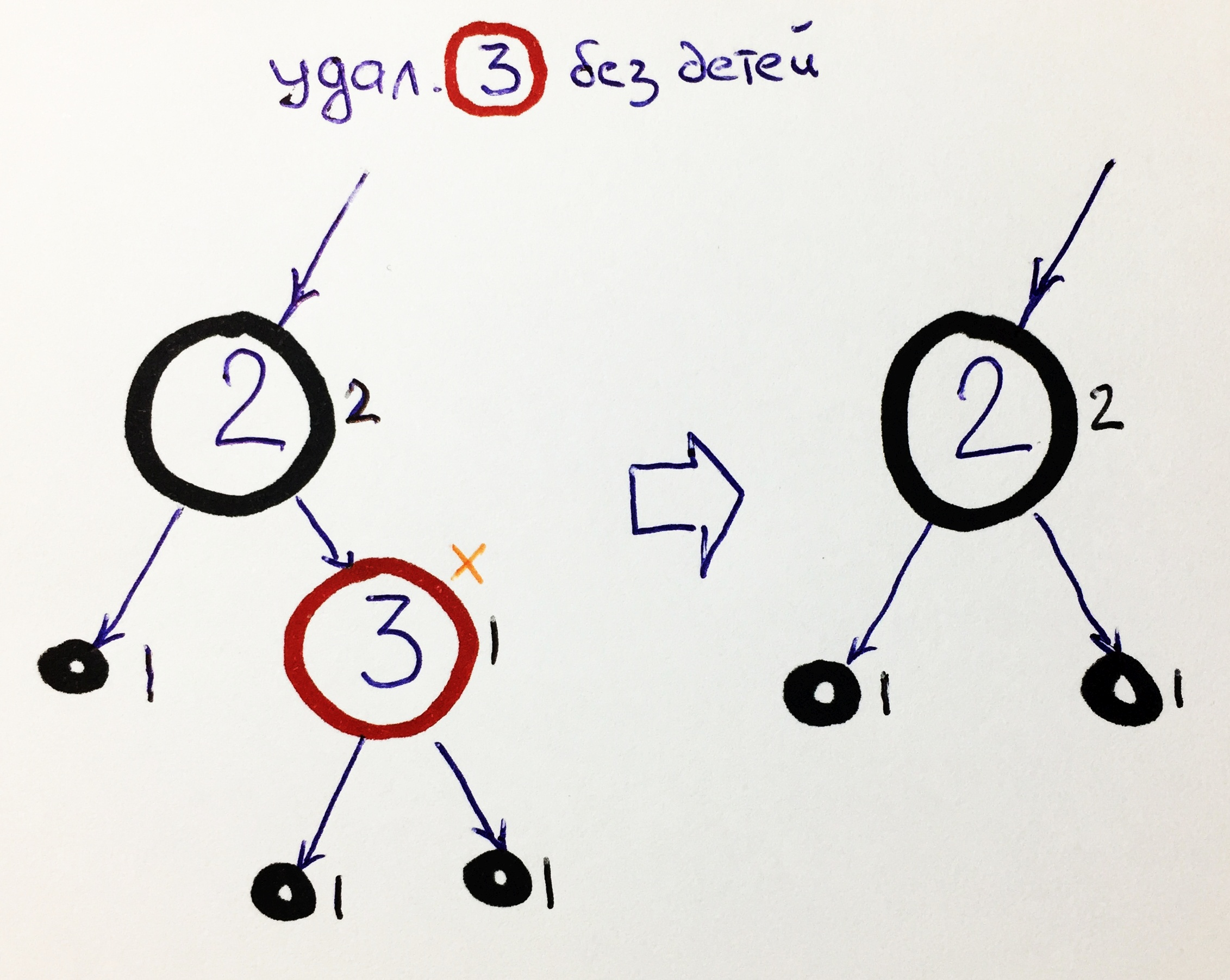
Eliminar el elemento rojo no cambia la altura del negro.
CH0 - nudo negro sin niños
Eliminar un nodo negro sin hijos también es muy simple: lo reemplazamos con una referencia a NIL.
¿Crees que esto es casi todo? Jaja, seis veces.

Después de eliminar el elemento negro, la altura de negro del subárbol cambia y debe equilibrarlo para su padre.
El elemento eliminado en las figuras se denota por x, su altura - h. Cuando comenzamos a equilibrar, h = 1, pero con llamadas recursivas puede aumentar.
Para ser más precisos, establezcamos que el elemento eliminado era el hijo correcto. Después de la remoción, su altura disminuyó y se convirtió en h. Esto significa que la altura del hijo izquierdo sigue siendo h + 1. Necesitamos alinear las alturas de los subárboles izquierdo y derecho y hacerlos iguales ah + 1.
Sugiero volver a dividir la tarea en varias partes. ¿Qué opciones tenemos?
El padre puede ser rojo o negro. El hijo izquierdo también puede ser negro o rojo. Y el hijo correcto siempre es negro; fue a partir de ahí que llegamos al equilibrio después de la remoción.
Hay 6 casos diferentes a considerar:
- KCH1 y KCH2: el padre es rojo, el hijo izquierdo es negro.
- CHK3 y CHK4: el padre es negro, el hijo izquierdo es rojo.
- HH5 y HH6: el padre es negro, el hijo izquierdo es negro.
Nos abasteceremos de paciencia y palomitas de maíz, lo más interesante y misterioso nos espera.
KCH1 - padre rojo, hijo izquierdo negro con nietos negros
Mientras tengamos los nodos rojos, podemos moverlos y / o cambiarles el color para restaurar el equilibrio de la altura del negro. En este caso, podemos reducir el color rojo del padre al hijo izquierdo, alineando así la altura negra del padre:

asegúrese de verificar en la figura que las alturas negras de los nodos ayb se conservan, y la altura de todo el subárbol se ha vuelto igual e igual a h + 1.
KCH2: el padre es rojo, el hijo izquierdo es negro con el nieto rojo izquierdo.
En este caso, repintar por sí solo no es suficiente. Necesitamos hacer un pequeño giro a la derecha entre los nodos 3-7. Como resultado, podremos aumentar la altura del subárbol derecho hasta h + 1: un
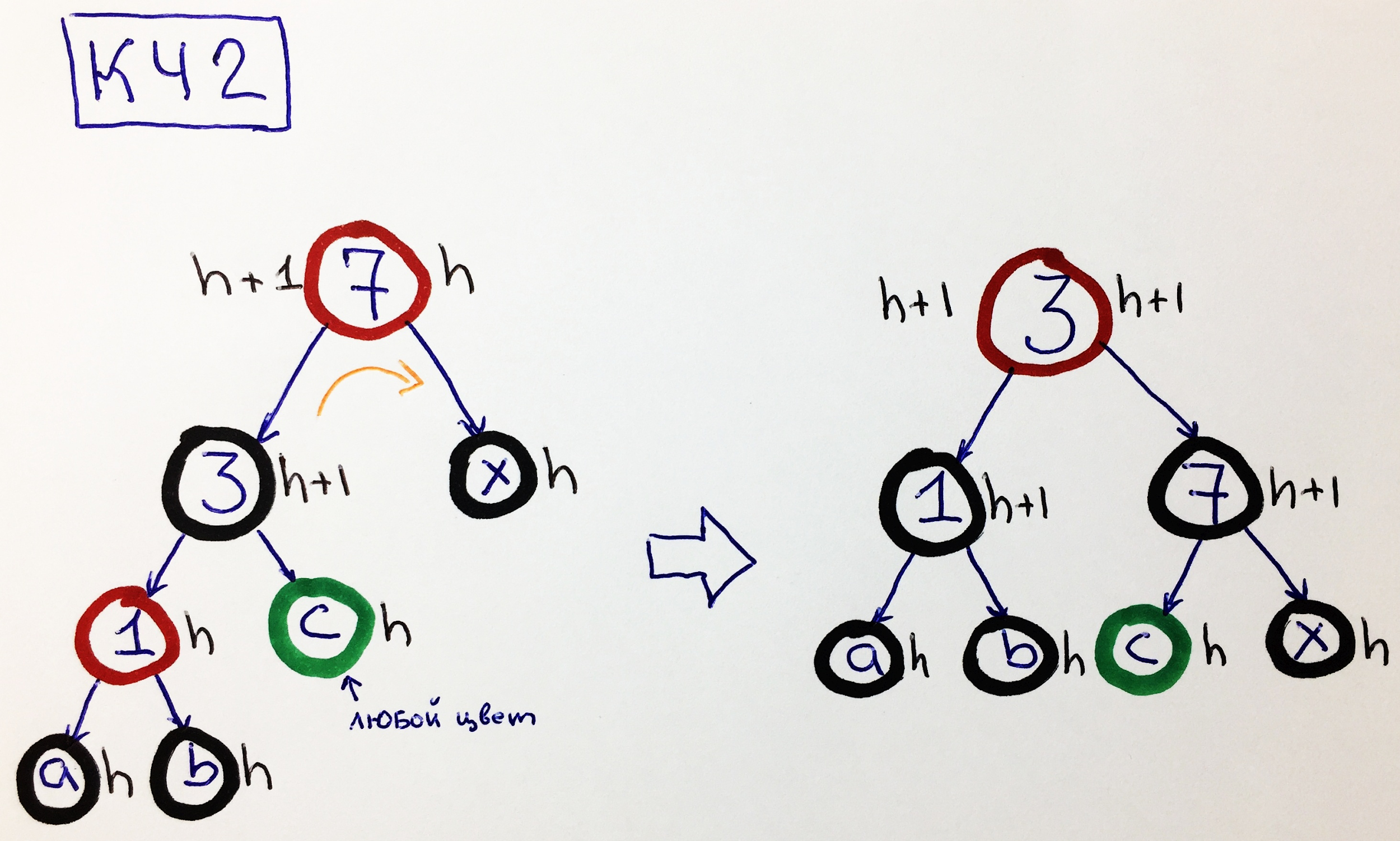
nodo verde significa que puede ser negro o rojo.
Nota. Si el nodo "1" es negro y "c" es rojo, entonces el problema se puede reducir a la variante HH5.
CHK3 - el padre es negro, el hijo izquierdo es rojo, el nieto derecho tiene bisnietos negros
Tener bisnietos negros le permite volver a pintar al nieto en rojo y enviarlo al subárbol correcto haciendo un pequeño giro a la derecha 3-7, y no pregunte por qué, solo confíe y verifique que la altura del negro se haya estabilizado: tenga en
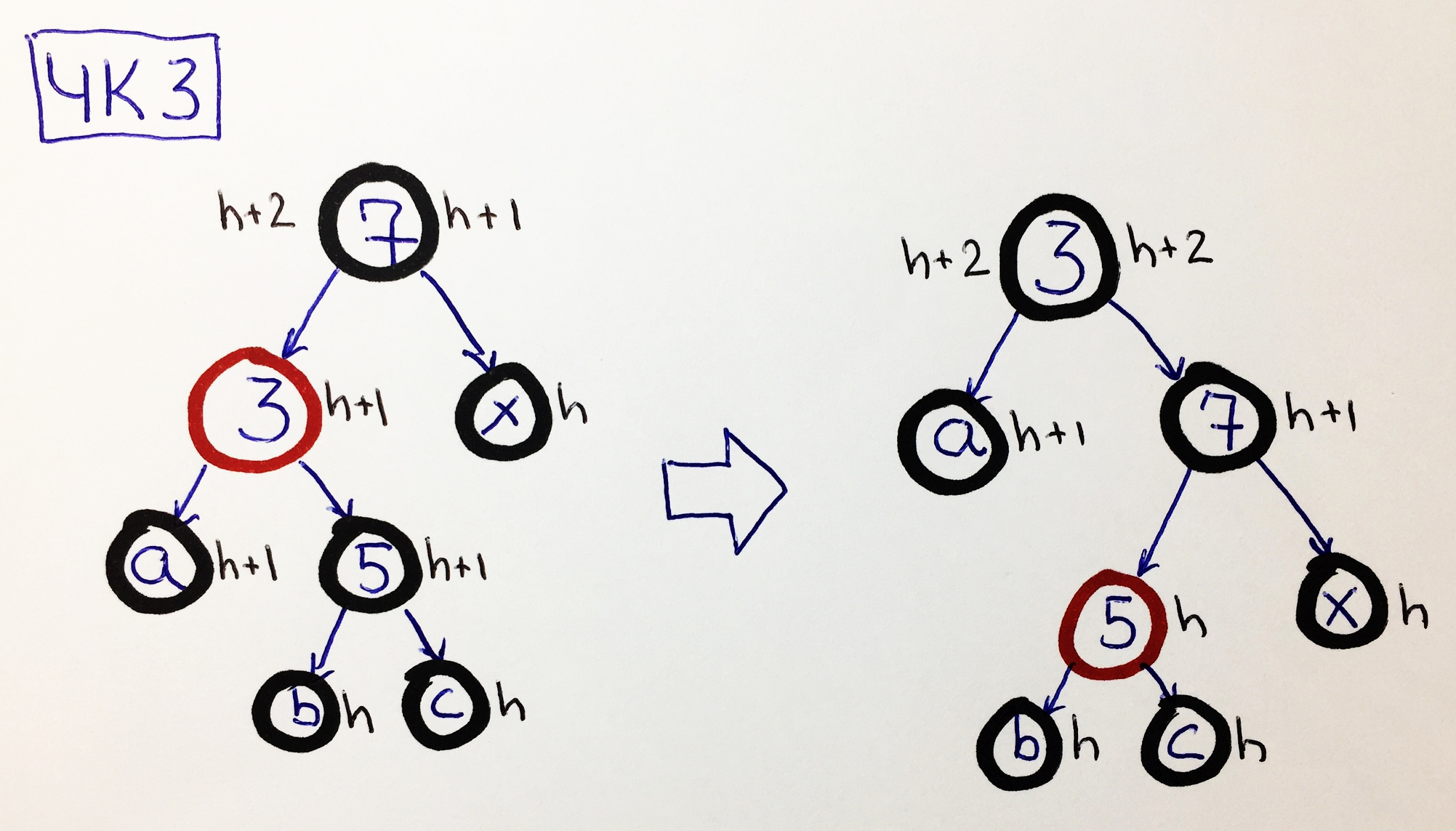
cuenta que el nodo rojo 5 no aumenta el negro altura.
CHK4: el padre es negro, el hijo izquierdo es rojo, el nieto derecho tiene un bisnieto rojo
Más adentro del bosque rojo, hay más leña negra y cada vez menos roja, es decir, al cambiar el color de los nodos rojos, es posible estabilizar la altura negra.

En este caso, debe hacer un gran giro a la izquierda, que consta de dos pequeños giros 5-3 y 5-7. El nodo b cambió su color de rojo a negro y, por lo tanto, aumentó su altura en 1. Asegúrese de que la altura del negro se haya estabilizado.
HCH5 - el padre es negro, el hijo izquierdo es negro con el nieto rojo derecho.
Cada vez menos elementos rojos en nuestro subárbol, repintar el último nieto rojo de negro y hacer un gran giro a la izquierda, como en el caso anterior.

Verifique que la altura negra del subárbol se haya estabilizado.
HCH6: el padre es negro, el hijo izquierdo es negro, sus nietos también son negros
Y luego llegó el momento en que se acabó la madera roja. No hay nada que hacer, tienes que pintar el nodo negro de rojo y así igualar la altura del negro del nodo 7, pero no aumentando la altura del negro del subárbol derecho, sino disminuyendo la altura del negro del subárbol izquierdo. Como resultado, la altura negra de toda nuestra estructura disminuirá en 1 y debemos llamar recursivamente el equilibrio a los antepasados.

Ejemplo de eliminación con equilibrio y recursividad
Observamos los 6 casos de equilibrio de altura de negro después de eliminar un elemento del árbol rojo-negro. Para tener una mejor idea de cómo funciona todo esto, continuemos eliminando el nodo 30 del árbol original.
El primer paso - simplemente quitar el nodo 30.
El segundo paso - correr balanceado sobre su padre - un nodo 25.
Hay un caso CHCH6:

Con dolor en la mitad de la altura de la unidad estabilizada 25.
El tercer paso - abuelo en el nivel de equilibrio - para el nodo 20.
Para hacerlo más divertido y más evidente , dibujemos todo el árbol antes y después del equilibrio. Este es el caso de HK4: observe

cómo el árbol rojo-negro cambió después del equilibrio, algunos de los elementos del subárbol izquierdo se movieron hacia la derecha, la altura se estabilizó, el elemento se eliminó, ¡todos están felices!
Eliminar elementos de un árbol rojo-negro es una de las operaciones más difíciles cuando se trabaja con árboles de búsqueda binarios. En el curso " Algoritmos y estructuras de datos " consideramos no solo árboles de búsqueda binarios, sino también muchos otros algoritmos interesantes, para más detalles ver el programa del curso.
