Los matemáticos llevan mucho tiempo tratando de acostumbrarse al hecho de que algunos problemas, en principio, no pueden resolverse.

Nos gusta decir que todo es posible. En el libro de Jaster Norton "Cute and the Magic Booth", el rey se niega a decirle a Milo que su objetivo es inalcanzable, porque "muchas cosas se vuelven posibles si no sabes que es imposible" [ aunque estas son las palabras de otros personajes del libro / aprox. transl. ]. Pero en el mundo real, algunas cosas son realmente imposibles y podemos probarlo con matemáticas.
La gente usa el término "imposible" de muchas formas diferentes. Puede describir las cosas poco probables, como encontrar dos mazos idénticos de cartas barajadas. Puede describir tareas que son casi imposibles debido a la falta de tiempo, espacio o recursos, como reescribir toda la Biblioteca del Congreso a mano. Los dispositivos como las máquinas de movimiento perpetuo son físicamente imposibles, ya que su existencia sería contraria a nuestra comprensión de la física.
La imposibilidad matemática es diferente. Comenzamos con suposiciones inequívocas y, utilizando el razonamiento matemático y la lógica, llegamos a la conclusión de que algunos resultados son imposibles. Ninguna cantidad de suerte, persistencia, tiempo o habilidad hará que la tarea sea factible. La historia de las matemáticas está repleta de pruebas de imposibilidad. Muchos de estos se consideran los resultados más notables de las matemáticas. Pero no siempre fue así.
El castigo, quizás la primera prueba de imposibilidad, fue estricto. Los historiadores creen que en el siglo V a. C. Hippasus de Metapont, un seguidor de Pitágoras, descubrió que era imposible encontrar un segmento de línea que pudiera medir tanto la longitud lateral como la diagonal de un pentágono regular. Hoy decimos que la longitud de la diagonal de un pentágono regular con una longitud de lado 1 es la proporción áurea, ϕ = 1/2 (1 + √5) - es un número irracional. El descubrimiento de Hippas fue un desafío al credo pitagórico, "todo es número", por lo que las leyendas dicen que Hippasus fue ahogado en el mar o simplemente expulsado de las filas de los pitagóricos.
Más de un siglo después, Euclides elevó la línea y el círculo como curvas fundamentales de la geometría. Posteriormente, muchas generaciones de geómetras dibujaron todo tipo de cosas (dividir ángulos, dibujar perpendiculares, etc.) solo con la ayuda de un compás y una regla. Sin embargo, ciertas estructuras, que parecían simples, desconcertaron a los geómetras griegos, adquirieron un estatus mítico como resultado y molestaron a los matemáticos durante más de 2000 años. Estos son los problemas de dividir un ángulo arbitrario en tres partes, construir el lado de un cubo, cuyo volumen es el doble del volumen dado, construir todos los polígonos regulares y también construir un cuadrado con un área igual al área de un círculo dado.
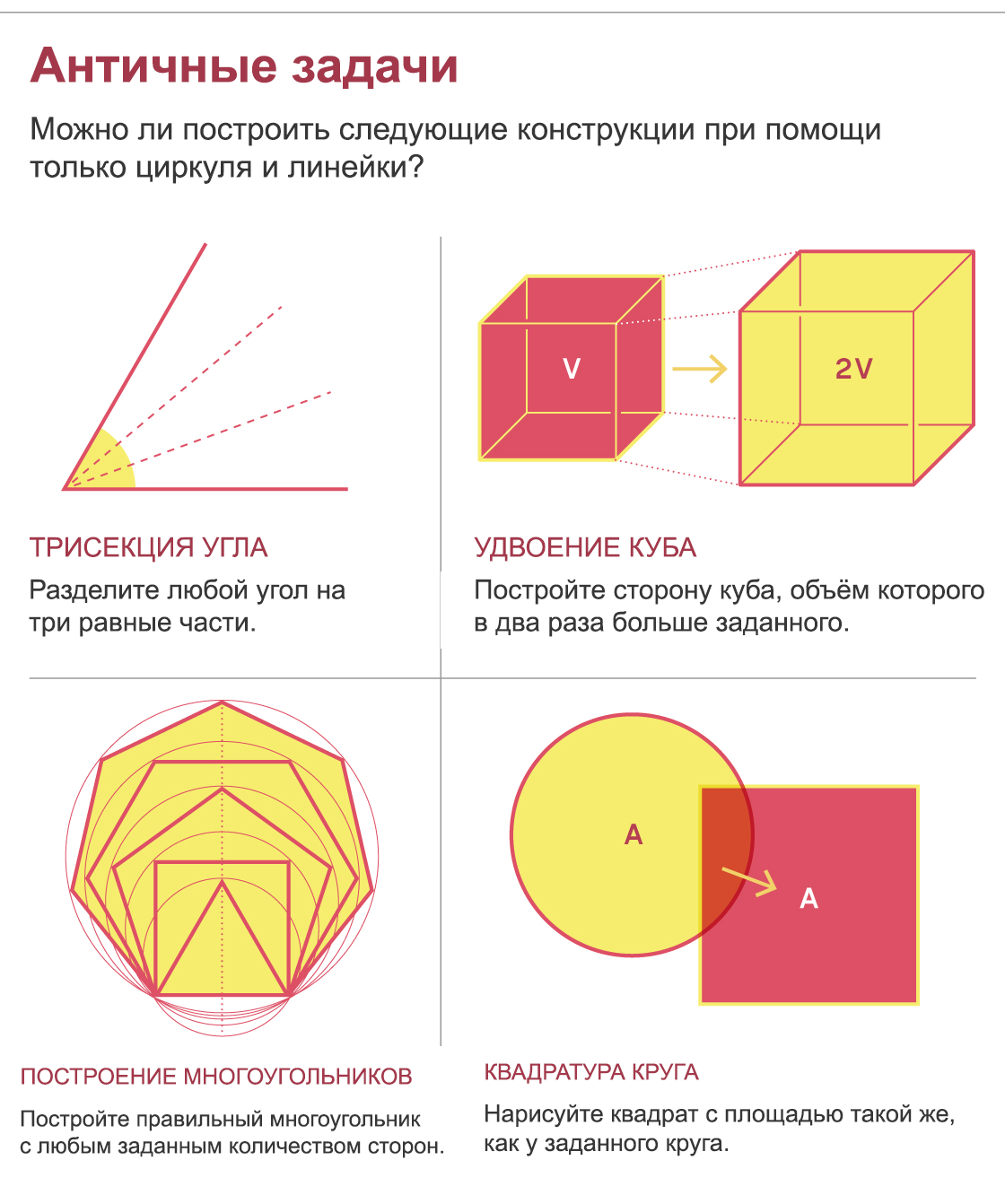
Aunque estos problemas son de naturaleza geométrica, la prueba de que no se pueden resolver no lo es. Se requirieron nuevas matemáticas para demostrar la imposibilidad de resolverlos.
En el siglo XVII, René Descartes hizo un descubrimiento fundamental: si nos limitamos a un compás y una regla, no podemos dibujar segmentos de ninguna longitud. Si comenzamos con una línea de longitud 1, solo podemos construir líneas cuya longitud se pueda expresar usando números enteros, suma, resta, multiplicación, división y raíz cuadrada (como la proporción áurea).
Por tanto, una de las estrategias para encontrar una prueba de la imposibilidad de resolver un problema geométrico, es decir, que un determinado objeto no se puede construir, será demostrar que la longitud de un determinado segmento de la figura final no se puede expresar de esta forma. Pero para mostrar esto de manera rigurosa, se requería el álgebra emergente en ese momento.
Dos siglos después, el compatriota de Descartes, Pierre Laurent Vanzel , utilizó polinomios (sumas de coeficientes y variables elevadas a una potencia) y sus raíces (variables que hacen que el polinomio sea igual a cero) para atacar estos problemas clásicos. Por ejemplo, en el problema de doblar un cubo, el lado de un cubo con un volumen dos veces mayor que el de una unidad de cubo debe ser igual a... Esta es la raíz del polinomio x 3 -2 porque...
En 1837, Wanzel demostró que para que un segmento se construya con un compás y una regla, su longitud debe ser la raíz de un polinomio que no se puede factorizar y cuyo grado (el grado más alto de la variable) es una potencia de dos. Por ejemplo, la proporción áurea es la raíz del polinomio de segundo grado x 2 - x - 1. Pero x 3 -2 es un polinomio de tercer grado, entoncesno se puede construir. Entonces Wanzel concluyó que doblar el cubo era imposible.
De manera similar, demostró que es imposible usar herramientas clásicas para trisecar cualquier ángulo o construir ciertos polígonos regulares, por ejemplo, uno de siete lados. Curiosamente, las tres pruebas de imposibilidad se publicaron en la misma página. Así como Isaac Newton y Albert Einstein tuvieron su annus mirabilis (años de milagros), esta situación puede llamarse pagina mirabilis, una página de milagros.
Probar la imposibilidad del problema restante, cuadrar el círculo, requería algo nuevo. En 1882 Ferdinand von Lindemanndemostró el punto clave - que el número π no se puede construir - demostrando su trascendencia, es decir, que no es raíz de ningún polinomio.
Estos problemas clásicos se pueden atribuir a una mala reputación y se consideran sirenas que atrajeron a los matemáticos a estrellarse contra las afiladas rocas de la imposibilidad. Pero creo que son musas que han inspirado a generaciones de pensadores creativos.
Lo mismo se aplica a la nueva tarea imposible que surge de un acto tan simple como cruzar un puente. Imagina que vives en Pittsburgh, la "ciudad de los puentes", como muchos de mis estudiantes. Cualquier ciclista aventurero podría preguntarse si comenzar un viaje desde casa puede cruzar cada uno de los 22 puentes que cruzan los principales ríos de Pittsburgh exactamente una vez y regresar a casa.
En 1735, el alcalde prusiano estableció una tarea similar para Leonard Euler, solo para Königsberg (ahora Kaliningrado). Siete puentes de esta ciudad conectan las tres orillas del río y la isla. Al principio, Euler descartó este problema por no considerarlo matemático: "Las soluciones de este tipo tienen poco que ver con las matemáticas y no entiendo por qué esperas que un matemático te las dé a ti y no a otra persona".
Sin embargo, pronto Euler demostró la imposibilidad de resolver este problema y en el proceso creó una nueva área de las matemáticas, a la que llamó geometría de arreglos, lo que hoy llamamos topología. Se dio cuenta de que los detalles específicos: la ubicación exacta de los puentes, la forma de las parcelas de tierra, etc. - no eran importantes. Solo sus conexiones eran importantes. Más tarde, los matemáticos refinaron las formulaciones de Euler usando lo que hoy llamamos gráficos. La idea de conectividad está en el centro del aprendizaje sobre redes sociales, Internet, epidemiología, lingüística, planificación de rutas y más.
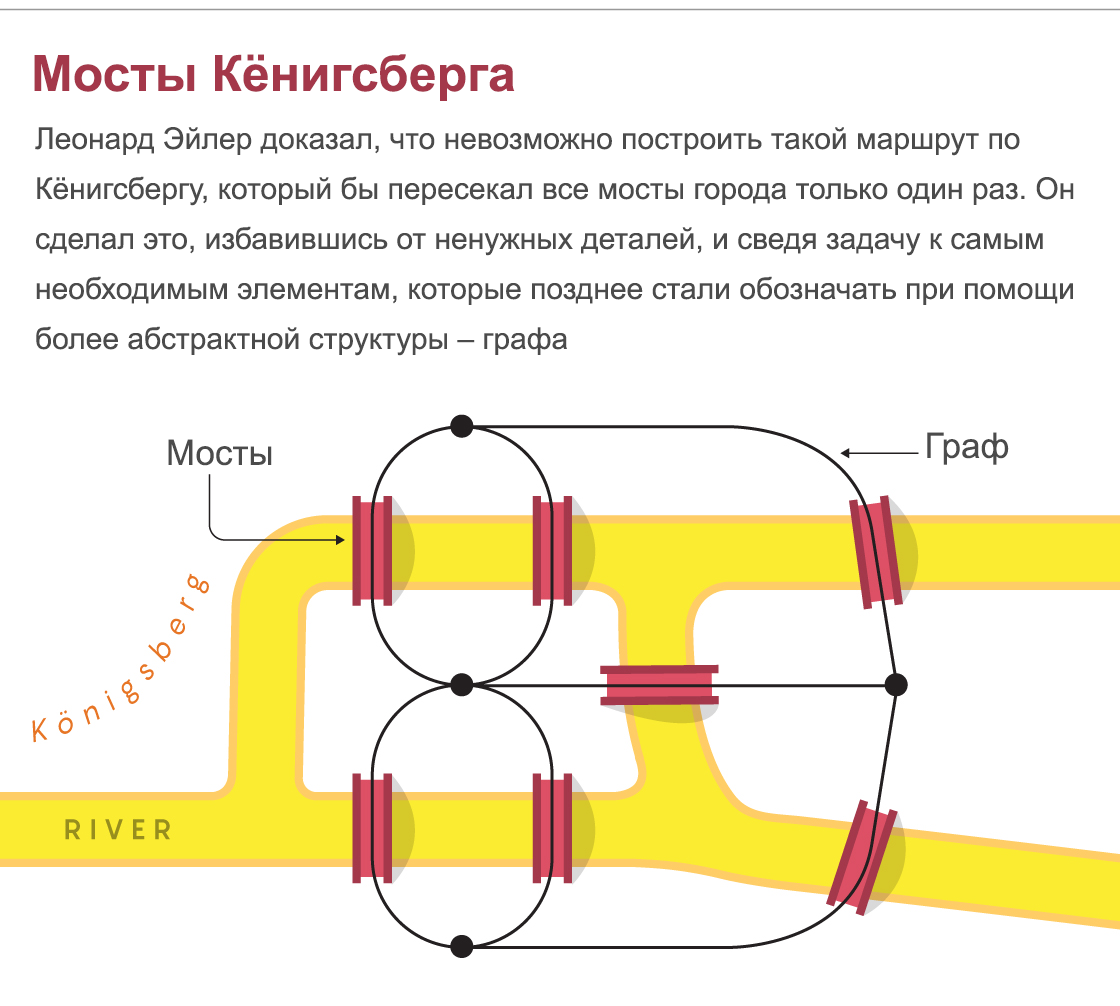
Puentes de Königsberg: Leonard Euler demostró que es imposible construir una ruta a lo largo de Königsberg que atraviese todos los puentes de la ciudad una sola vez. Lo hizo deshaciéndose de los detalles innecesarios y reduciendo la tarea a los elementos más necesarios, que luego comenzaron a designarse utilizando una estructura más abstracta: el gráfico.
La prueba de Euler fue sorprendentemente simple. Razonó que cada vez que entramos y luego dejamos un terreno en particular, debemos eliminar dos puentes. Por lo tanto, se debe conectar un número par de puentes a cada terreno. Pero dado que un número impar de puentes conducía a cada sección de Königsberg, fue imposible construir una ruta así. Asimismo, los tres puentes que conducen a la isla Gers en el río Allegheny en Pittsburgh hacen imposible construir la ruta ciclista deseada.
Como muestra este problema, las imposibilidades no se limitan a las matemáticas abstractas. Pueden tener consecuencias en el mundo real, a veces incluso políticas.
Recientemente, los matemáticos han recurrido al concepto de manipulación . En los Estados Unidos, después de cada censo, los estados deben rehacer los distritos electorales. Pero a veces el partido gobernante reescribe sus fronteras de formas ridículas para maximizar su poder político.
Muchos estados tienen un requisito de distritos "compactos" que no tienen una definición matemática estricta. En 1991 Daniel Paulsby y Robert Popper propusieron 4πA / P 2como una forma de medir la compacidad del área A y el perímetro P. Estos valores van desde 1 para una parroquia redonda hasta casi cero para condados deformados con un perímetro largo.
Mientras tanto, Nicholas Stephanopoulos y Eric McGee introdujeron la “brecha de desempeño” en 2014 como una medida de la integridad política de un plan de cambio de distrito. Dos estrategias diferentes de manipulación de derechos son que la oposición en el distrito electoral tenga menos del 50% de los votos o alrededor del 100%. Cada una de estas tácticas hace que la oposición pierda votos al perder a los candidatos adecuados o desperdiciar votos en los que no lo hacen. La brecha de eficiencia describe el número relativo de votos perdidos.
Ambas medidas son útiles para reconocer el gerrymandering. Pero en 2018 Boris Alekseev y Dustin Mixondemostró que "a veces se pueden lograr pequeñas brechas de eficiencia con condados de formas extrañas". Es decir, es matemáticamente imposible dibujar siempre condados para satisfacer tanto los requisitos de Paulsby-Popper como la integridad de la brecha de eficiencia.
Sin embargo, la detección y prevención de técnicas de manipulación subrepticia es un campo en rápido crecimiento que atrae muchos esfuerzos de investigación talentosos. Al igual que con los problemas de la antigüedad o el problema de los puentes de Königsberg, estoy seguro de que el problema del gerrymandering inspirará creatividad y contribuirá al desarrollo de las matemáticas.