
Esta semana (16 al 26 de septiembre) en San Petersburgo (virtualmente) comenzó la 61ª Olimpiada Internacional de Matemáticas , en la que participan 622 escolares de 114 países.
La primera Olimpiada de este tipo se celebró en 1959 en Rumania, y luego participaron en ella representantes de solo siete países.
Rusia está representada por un equipo de seis estudiantes de secundaria.
Los escolares tienen 2 días de 4,5 horas para resolver 6 problemas. Mientras se evalúan los resultados, le sugiero que intente resolver los problemas y discutirlos en los comentarios.
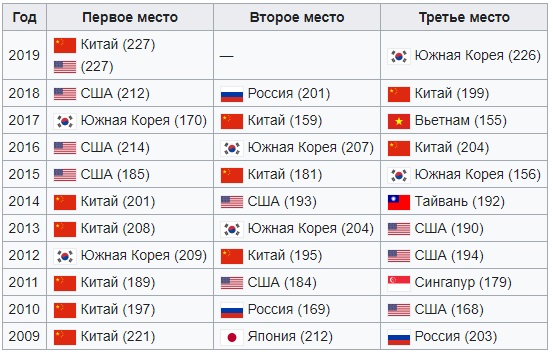
Resultados de años pasados.
Problema 1
Dentro del cuadrilátero convexo ABCD, hay un punto P tal que las igualdades
∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC se mantienen.
Demuestre que las siguientes tres líneas rectas se encuentran en un punto: las bisectrices internas de los ángulos ∠ADP y ∠PCB y el punto medio perpendicular al segmento AB.
Problema 2
Dados los números reales a, b, c, d tales que a> b> c> d> 0 y a + b + c + d = 1.
Demuestre que
(a + 2b + 3c + 4d) a a b b c c d d <1.
Problema 3
Hay 4n guijarros con masas 1, 2, 3, ..., 4n . Cada uno de los guijarros está coloreado en uno de n colores, y hay 4 guijarros de cada color.
Demuestre que las piedras se pueden dividir en dos montones de igual peso total para que cada montón contenga dos piedras de cada color.
Problema 4
Se da un número entero n> 1 . Hay n 2 estaciones de funicular en la pendiente a diferentes alturas. Cada una de las dos compañías de funiculares A y B posee k ascensores. Cada ascensor realiza un traslado directo regular desde una de las estaciones a otra estación superior. Las k transferencias de la empresa A comienzan en k estaciones diferentes; también terminan en k estaciones diferentes; con una transferencia que comienza arriba y termina arriba. Se cumplen las mismas condiciones para la empresa B. Diremos que dos estaciones están conectadasempresa de funicular, si se puede llegar desde la estación inferior a la superior utilizando uno o más traslados de esta empresa (otros traslados entre estaciones están prohibidos) Encuentre el k más pequeño para el que se sabe que hay dos estaciones conectadas por ambas compañías.
Problema 5
Hay n> 1 cartas, cada una de las cuales contiene un número entero positivo.
Resultó que, para dos tarjetas cualesquiera, la media aritmética de los números escritos en ellas es igual a la media geométrica de los números escritos en las tarjetas de un determinado conjunto que consta de una o más tarjetas. ¿De qué n se sigue que todos los números escritos en las tarjetas son iguales?
Problema 6
Demuestre que existe una constante positiva c para la cual se cumple el siguiente enunciado:
Sea S un conjunto de n> 1 puntos del plano en el que la distancia entre dos puntos cualesquiera es al menos 1. Entonces hay una línea ℓ que separa el conjunto S tal que la distancia desde cualquier los puntos S a ℓ son al menos cn −1/3 .
(La línea recta ℓ separa el conjunto de puntos S si intersecta algún segmento cuyos extremos pertenecen a S.)
Observación. Los resultados más débiles con cn −1/3 reemplazado por cn −α se pueden estimar dependiendo del valor de la constante α> 1/3 .