Hola, mi nombre es David, y aquí estoy yo mismo, interpretado por mi propio render pintado a mano:





Desafortunadamente, no pude encontrar un modelo gratuito de mejor calidad , ¡pero aún expreso mi gratitud al escultor extranjero que me capturó en digital! Y como habrás adivinado, hablaremos sobre cómo escribir una CPU: render.

Idea

Con el desarrollo de lenguajes de sombreado y el aumento de la potencia de la GPU, cada vez más personas están interesadas en la programación de gráficos. Han aparecido nuevas direcciones, como la marcha de Ray con un rápido crecimiento en su popularidad.



Anticipándome al lanzamiento de un nuevo monstruo de NVidia, decidí escribir mi propio artículo (de tubo y de la vieja escuela) sobre los conceptos básicos del renderizado en una CPU. Es un reflejo de mi experiencia personal al escribir un render, y en él intentaré transmitir los conceptos y algoritmos que encontré en el proceso de codificación. Debe entenderse que el rendimiento de este software será muy bajo debido a la inadecuación del procesador para realizar tales tareas.



La elección del idioma inicialmente recayó en c ++ o rust , pero me decidí por c #debido a la facilidad de escribir código y las amplias oportunidades de optimización. El producto final de este artículo será un render capaz de producir imágenes como esta:







Todos los modelos que utilicé aquí se distribuyen en el dominio público, ¡no piratees y respeta el trabajo de los artistas!

Matemáticas

No hace falta decir dónde escribir renders sin comprender sus fundamentos matemáticos. En esta sección, solo cubriré los conceptos que usé en el código. No recomiendo a aquellos que no estén seguros de sus conocimientos que se salten esta sección, sin comprender estos conceptos básicos será difícil comprender la presentación posterior. También espero que quien haya decidido estudiar geometría computacional tenga conocimientos básicos en álgebra lineal, geometría, así como trigonometría (ángulos, vectores, matrices, producto escalar). Para aquellos que quieran comprender la geometría computacional más profundamente, puedo recomendar el libro de E. Nikulin "Computer Geometry and Computer Graphics Algorithms" .

Giros vectoriales. Matriz de rotación

La rotación es una de las transformaciones lineales básicas del espacio vectorial. También es una transformación ortogonal, ya que conserva las longitudes de los vectores transformados. Hay dos tipos de rotaciones en el espacio 2D:

• Rotación relativa al origen
• Rotación sobre algún punto

Aquí consideraré solo el primer tipo, ya que el segundo es una derivada del primero y difiere solo en el cambio del sistema de coordenadas de rotación (analizaremos más el sistema de coordenadas).



Derivemos fórmulas para rotar un vector en un espacio bidimensional. Denotemos las coordenadas del vector original - {x, y} . Las coordenadas del nuevo vector, rotado por el ángulo f , se denotarán como {x 'y'} .





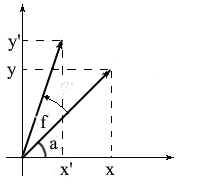
Sabemos que la longitud de estos vectores es común y por lo tanto podemos usar los conceptos de coseno y seno para expresar estos vectores en términos de longitud y ángulo alrededor del eje OX :





Tenga en cuenta que podemos usar las fórmulas de suma y coseno para expandir los valores x ' e y' . Para aquellos que lo han olvidado, les recordaré estas fórmulas:





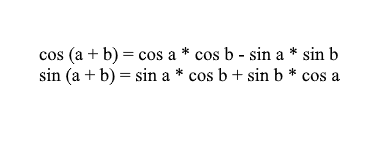
Al expandir las coordenadas del vector girado a través de ellas, obtenemos:





Es fácil ver aquí que los factores l * cos a y l * sin a son las coordenadas del vector original: x = l * cos a, y = l * sin a . Vamos a reemplazar con X y Y :





Por lo tanto, expresamos el vector girado a través de las coordenadas del vector original y el ángulo de su rotación. Como matriz, esta expresión se verá así:





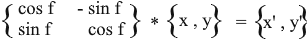
Multiplica y comprueba que el resultado sea equivalente a lo que dedujimos.

Rotar en el espacio 3D

Hemos considerado la rotación en el espacio bidimensional y también hemos derivado una matriz para ella. Ahora surge la pregunta, ¿cómo obtener tales transformaciones para tres dimensiones? En el caso bidimensional, rotamos vectores en un plano, pero aquí hay un número infinito de planos en relación con los cuales podemos hacer esto. Sin embargo, hay tres tipos básicos de rotaciones con las que puede expresar cualquier rotación de un vector en un espacio tridimensional: estas son las rotaciones XY , XZ , YZ . Rotación



XY .



Con esta rotación, rotamos el vector sobre el eje OZ del sistema de coordenadas. Imagina que los vectores son las palas del helicóptero y el eje OZ es el mástil al que se aferran. Con XYLa rotación del vector girará alrededor del eje OZ , como las palas de un helicóptero en relación con el mástil.





Tenga en cuenta que con esta rotación, los z coordenadas de los vectores no cambian, pero la x y x coordenadas cambio - por eso esto se llama el XY rotación.





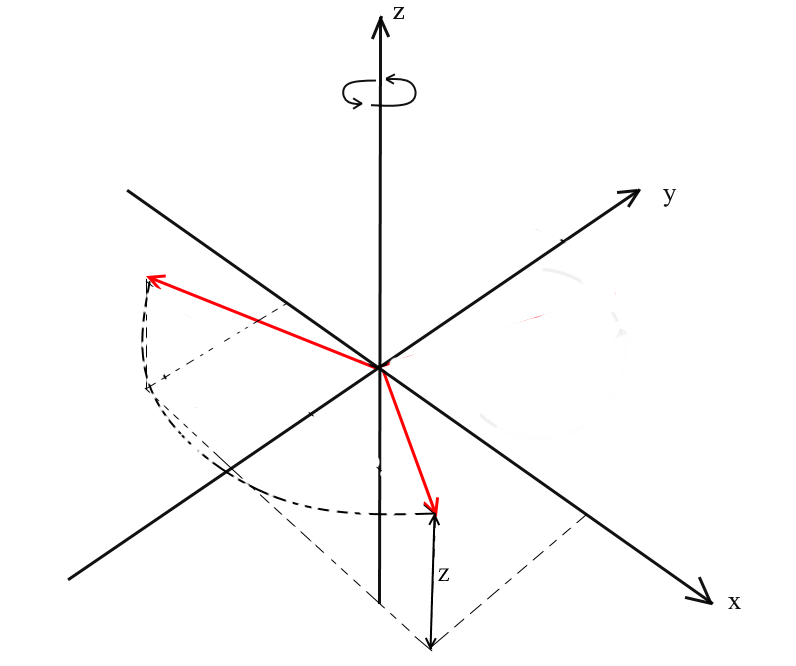
No es difícil de fórmulas Derivar para tal una rotación: z - los restos de coordenadas de la misma, y x y y cambio de acuerdo con los mismos principios que en rotación 2D.





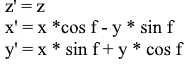
Lo mismo en forma de matriz:





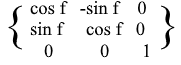
Para las rotaciones XZ e YZ , todo es igual:

Proyección

El concepto de proyección puede variar según el contexto en el que se utilice. Muchos probablemente hayan oído hablar de conceptos como proyección en un plano o proyección en un eje de coordenadas.



En el entendimiento que usamos aquí, la proyección sobre un vector también es un vector. Sus coordenadas son el punto de intersección de la perpendicular que cae del vector a al b con el vector b .





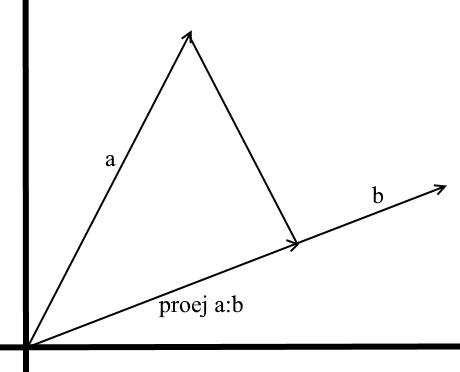
Para definir dicho vector, necesitamos conocer su longitud y dirección . Como sabemos, el cateto adyacente y la hipotenusa en un triángulo rectángulo están relacionados por la razón del coseno, por lo que la usamos para expresar la longitud del vector de proyección:





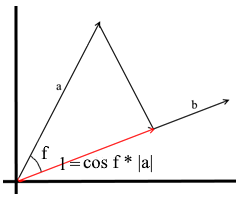
La dirección del vector de proyección por definición coincide con el vector b , lo que significa que la proyección está determinada por la fórmula:





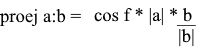
Aquí obtenemos la dirección de la proyección como un vector unitario y la multiplicamos por la longitud de la proyección. No es difícil entender que el resultado será exactamente lo que buscamos.



Ahora representemos todo en términos del producto escalar :





Obtenemos una fórmula conveniente para encontrar la proyección:

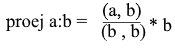
Sistemas coordinados. Bases

Muchos están acostumbrados a trabajar en el sistema de coordenadas XYZ estándar , en el que cualesquiera 2 ejes serán perpendiculares entre sí, y los ejes de coordenadas se pueden representar como vectores unitarios:





De hecho, existen infinitos sistemas de coordenadas, cada uno de ellos es una base . La base del espacio n -dimensional es un conjunto de vectores {v1, v2 …… vn} a través de los cuales se representan todos los vectores de este espacio. En este caso, ningún vector de la base puede representarse a través de sus otros vectores. De hecho, cada base es un sistema de coordenadas separado en el que los vectores tendrán sus propias coordenadas únicas.



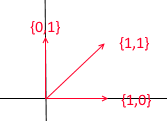
Echemos un vistazo a cuál es la base del espacio bidimensional. Tomemos, por ejemplo, el conocido sistema de coordenadas cartesianas de los vectores X {1, 0} , Y {0, 1} , que es una de las bases de un espacio bidimensional:







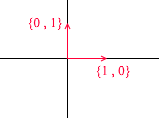
Cualquier vector en un plano se puede representar como una suma de vectores de esta base con ciertos coeficientes, o como una combinación lineal . Recuerde lo que hace cuando escribe las coordenadas de un vector: escribe x , la coordenada y luego y . Así es como se determinan realmente los coeficientes de expansión en términos de los vectores base.







Ahora tomemos otra base:







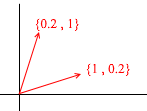
Cualquier vector 2D también se puede representar mediante sus vectores:







Pero tal conjunto de vectores no es la base de un espacio bidimensional:







En él, dos vectores {1,1} y {2,2} se encuentran en una línea recta. Cualesquiera que sean las combinaciones que tome, solo recibirá vectores que se encuentran en la línea recta común y = x . Para nuestros propósitos, estos defectuosos no serán útiles, sin embargo, creo que vale la pena comprender la diferencia. Por definición, todas las bases están unidas por una propiedad: ninguno de los vectores base puede representarse como una suma de otros vectores base con coeficientes, o ninguno de los vectores base es una combinación lineal de otros. Aquí hay un ejemplo de un conjunto de 3 vectores que tampoco es una base :







Cualquier vector de un plano bidimensional puede expresarse a través de él , pero el vector {1, 1} en él es superfluo, ya que él mismo puede expresarse a través de los vectores {1, 0} y {0,1} como {1,0} + {0,1 } .



En general, cualquier base de un espacio n- dimensional contendrá exactamente n vectores, para 2e este n es correspondientemente igual a 2.



Pasemos a 3d. La base tridimensional contendrá 3 vectores:







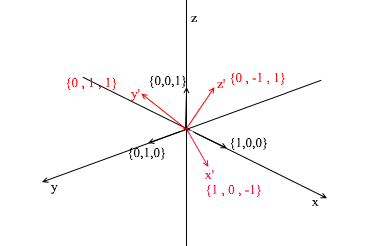
Si para una base bidimensional fue suficiente con dos vectores que no estén en una línea recta, entonces en un espacio tridimensional el conjunto de vectores será una base si:

• 1) 2 vectores no se encuentran en una línea recta
• 2) el tercero no se encuentra en el plano formado por los otros dos.

A partir de ahora, las bases con las que trabajemos serán ortogonales (cualquiera de sus vectores es perpendicular) y normalizadas (la longitud de cualquier vector base es 1). Simplemente no necesitaremos a otros. Por ejemplo, la base estándar







cumple estos criterios.

Transición a otra base

Hasta ahora, hemos escrito la descomposición de un vector como una suma de vectores base con coeficientes:





Considere nuevamente la base estándar: el vector {1, 3, 6} en él se puede escribir de la siguiente manera:





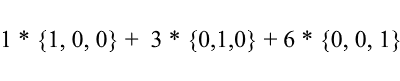
Como puede ver, los coeficientes de expansión de un vector en la base son sus coordenadas en esta base . Veamos el siguiente ejemplo:







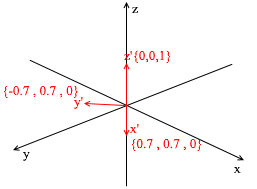
Esta base se deriva del estándar aplicándole una rotación XY de 45 grados. Tome un vector a en el sistema estándar con coordenadas {0, 1, 1}







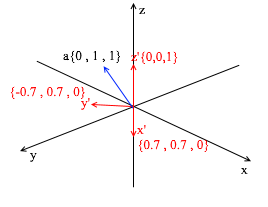
A través de los vectores de la nueva base, se puede expandir de la siguiente manera:







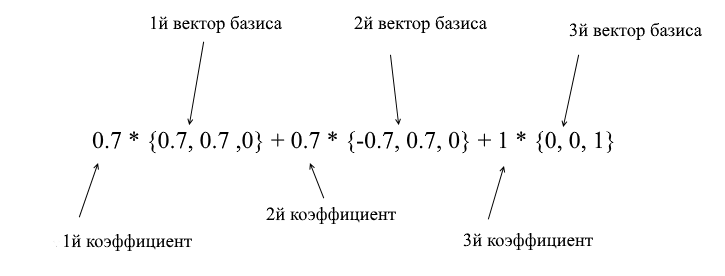
Si calcula esta cantidad, obtendrá {0, 1, 1} , el vector a en la base estándar. Basado en esta expresión en la nueva base, el vector a tiene coordenadas {0.7, 0.7, 1} - los coeficientes de expansión. Esto será más visible si miras desde un ángulo diferente:







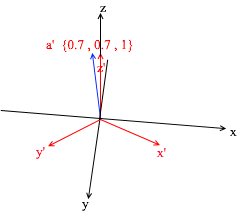
Pero, ¿cómo encuentras estos coeficientes? En general, un método universal es la solución de un sistema bastante complejo de ecuaciones lineales. Sin embargo, como dije antes, solo usaremos bases ortogonales y normalizadas , y para ellas hay una forma muy engañosa. Consiste en encontrar proyecciones sobre los vectores base. Usémoslo para encontrar la descomposición del vector a en la base X {0.7, 0.7, 0} Y {-0.7, 0.7, 0} Z {0, 0, 1}







Primero, encontremos el coeficiente para y ' . El primer paso es encontrar la proyección del vector a sobre el vector y ' (discutí cómo hacer esto anteriormente):







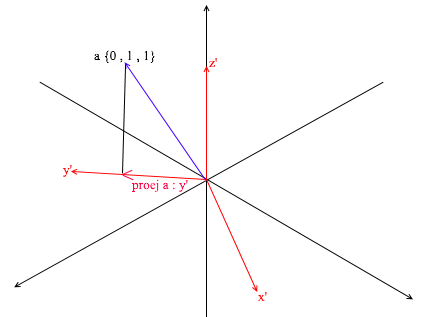
El segundo paso: dividimos la longitud de la proyección encontrada por la longitud del vector y ' , de ese modo averiguamos “cuántos vectores y' caben en el vector de proyección” - este número será el coeficiente para y ' , y también y - ¡la coordenada del vector a en la nueva base! Para x ' y z', repita operaciones similares:







Ahora tenemos fórmulas para la transición de una base estándar a una nueva:







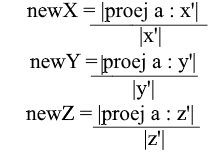
Bueno, dado que solo usamos bases normalizadas y las longitudes de sus vectores son iguales a 1, no habrá necesidad de dividir por la longitud del vector en la fórmula de transición:







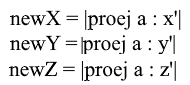
Expanda la coordenada x a través de la fórmula de proyección:







Tenga en cuenta que el denominador (x ', x') y el vector x ' en el caso de una base normalizada también son iguales a 1 y pueden descartarse. Obtenemos:







Vemos que la coordenada x en la base se expresa como el producto escalar (a, x ') , la coordenada y, respectivamente, como (a, y') , la coordenada z es (a, z ') . Ahora puede crear una matriz de transición a nuevas coordenadas:

Sistemas de coordenadas desplazadas

Todos los sistemas de coordenadas que consideramos anteriormente tenían el origen del punto {0,0,0} . Además, también hay sistemas con un punto de origen desplazado:







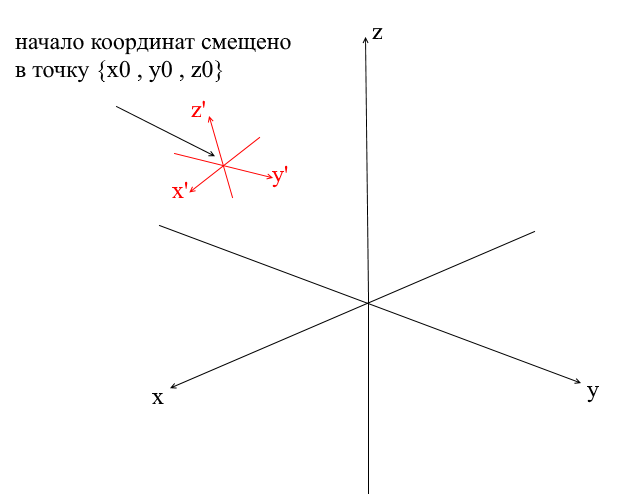
Para traducir un vector a tal sistema, primero debe expresarlo en relación con el nuevo centro de coordenadas. Hacer esto es simple: reste este centro del vector. Por lo tanto, "mueve" el sistema de coordenadas a un nuevo centro, mientras que el vector permanece en su lugar. A continuación, puede utilizar la matriz de transición que ya conocemos.

Escribiendo un motor de geometría. Crea un render similar a un cable.

Bueno, creo que a alguien que pasó por la sección de matemáticas y no cerró el artículo se le puede lavar el cerebro con cosas más interesantes. En esta sección, comenzaremos a escribir los conceptos básicos de un motor 3D y renderizado. En general, el renderizado es un procedimiento bastante complicado, que incluye muchas operaciones diferentes: cortar bordes invisibles, rasterizar, calcular la luz, procesar varios efectos, materiales (a veces incluso física). Analizaremos parcialmente todo esto en el futuro, pero ahora haremos cosas más simples: escribiremos un render de alambre . Su esencia es que dibuja un objeto en forma de líneas que conectan sus vértices, por lo que el resultado parece una red de cables:

Gráficos poligonales

Tradicionalmente, los gráficos por computadora utilizan representaciones poligonales de datos de objetos en 3D. Por lo tanto, los datos se presentan en OBJ, 3DS, FBX y muchos otros. En una computadora, dichos datos se almacenan en forma de dos conjuntos: un conjunto de vértices y un conjunto de caras (polígonos). Cada vértice de un objeto está representado por su posición en el espacio - un vector, y cada cara (polígono) está representada por tres números enteros que son índices de los vértices de este objeto. Los objetos más simples (cubos, esferas, etc.) consisten en tales polígonos y se denominan primitivas.



En nuestro motor, la primitiva será el objeto principal de la geometría 3D; todos los demás objetos heredarán de ella. Describamos la clase del primitivo:

    abstract class Primitive
    {
        public Vector3[] Vertices { get; protected set; }
        public int[] Indexes { get; protected set; }
    }

Hasta ahora, todo es simple: hay vértices de la primitiva y hay índices para formar polígonos. Ahora puedes usar esta clase para crear un cubo:

   public class Cube : Primitive
      {
        public Cube(Vector3 center, float sideLen)
        {
            var d = sideLen / 2;
            Vertices = new Vector3[]
                {
                    new Vector3(center.X - d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X - d , center.Y - d, center.Z) ,
                    new Vector3(center.X - d , center.Y , center.Z - d) ,
                    new Vector3(center.X - d , center.Y , center.Z) ,
                    new Vector3(center.X + d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y - d, center.Z) ,
                    new Vector3(center.X + d , center.Y + d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y + d, center.Z + d) ,
                };

            Indexes = new int[]
                {
                    1,2,4 ,
                    1,3,4 ,
                    1,2,6 ,
                    1,5,6 ,
                    5,6,8 ,
                    5,7,8 ,
                    8,4,3 ,
                    8,7,3 ,
                    4,2,8 ,
                    2,8,6 ,
                    3,1,7 ,
                    1,7,5
                };
        }
    }

int Main()
{
        var cube = new Cube(new Vector3(0, 0, 0), 2);
}

Implementando sistemas de coordenadas

No es suficiente configurar un objeto con un conjunto de polígonos; para planificar y crear escenas complejas, es necesario colocar objetos en diferentes lugares, rotarlos, reducirlos o aumentarlos de tamaño. Para la conveniencia de estas operaciones, se utilizan los denominados sistemas de coordenadas locales y globales . Cada objeto de la escena tiene su propio sistema de coordenadas: local, así como su propio punto central.





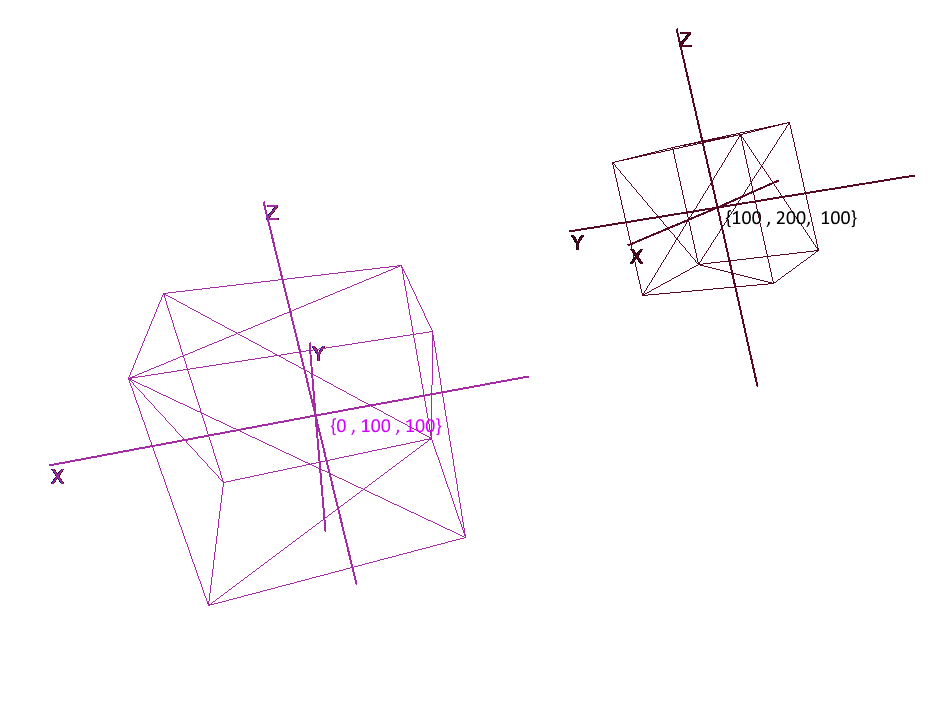
La representación de un objeto en coordenadas locales le permite realizar fácilmente cualquier operación con él. Por ejemplo, para mover un objeto por el vector a , será suficiente desplazar el centro de su sistema de coordenadas por este vector, para rotar un objeto - para rotar sus coordenadas locales.



Al trabajar con un objeto, realizaremos operaciones con sus vértices en el sistema de coordenadas local; durante el renderizado, primero traduciremos todos los objetos de la escena en un único sistema de coordenadas: el global. Agreguemos sistemas de coordenadas al código. Para hacer esto, cree un objeto de la clase Pivot (pivot, pivot point), que representará la base local del objeto y su punto central. La conversión de un punto a un sistema de coordenadas presentado por Pivot se realizará en 2 pasos:

• 1) Representación de un punto relativo al centro de nuevas coordenadas
• 2) Expansión en vectores de la nueva base

Por el contrario, para representar el vértice local de un objeto en coordenadas globales, debes realizar estas acciones en orden inverso:

• 1) Expansión en vectores de la base global
• 2) Representación relativa al centro global

Escribamos una clase para representar sistemas de coordenadas:

    public class Pivot
    {
        // 
        public Vector3 Center { get; private set; }
        //   -   
        public Vector3 XAxis { get; private set; }
        public Vector3 YAxis { get; private set; }
        public Vector3 ZAxis { get; private set; }

        //    
        public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
            (
                XAxis.X, YAxis.X, ZAxis.X,
                XAxis.Y, YAxis.Y, ZAxis.Y,
                XAxis.Z, YAxis.Z, ZAxis.Z
            );

        //    
        public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
            (
                XAxis.X , XAxis.Y , XAxis.Z,
                YAxis.X , YAxis.Y , YAxis.Z,
                ZAxis.X , ZAxis.Y , ZAxis.Z
            );

        public Vector3 ToLocalCoords(Vector3 global)
        {
            //          
            return LocalCoordsMatrix * (global - Center);
        }
        public Vector3 ToGlobalCoords(Vector3 local)
        {
            //    -            
            return (GlobalCoordsMatrix * local)  + Center;
        }

        public void Move(Vector3 v)
        {
            Center += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            XAxis = XAxis.Rotate(angle, axis);
            YAxis = YAxis.Rotate(angle, axis);
            ZAxis = ZAxis.Rotate(angle, axis);
        }
    }

Ahora, usando esta clase, agregue las funciones de rotación, movimiento y aumento a las primitivas:

    public abstract class Primitive
    {
        //  
        public Pivot Pivot { get; protected set; }
        // 
        public Vector3[] LocalVertices { get; protected set; }
        // 
        public Vector3[] GlobalVertices { get; protected set; }
        // 
        public int[] Indexes { get; protected set; }

        public void Move(Vector3 v)
        {
            Pivot.Move(v);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            Pivot.Rotate(angle , axis);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }

        public void Scale(float k)
        {
            for (int i = 0; i < LocalVertices.Length; i++)
                LocalVertices[i] *= k;

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }
    }

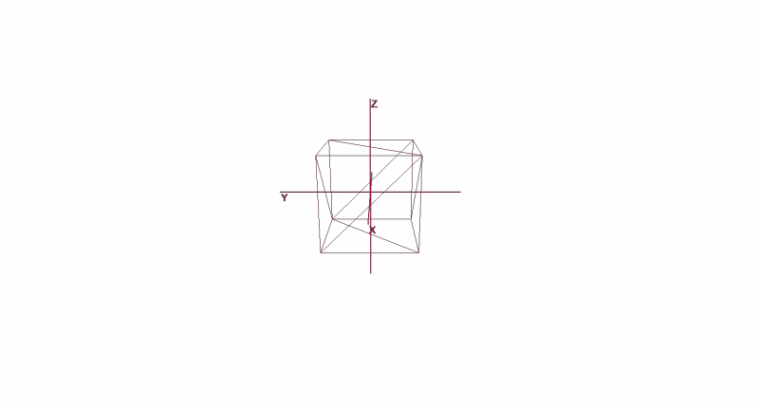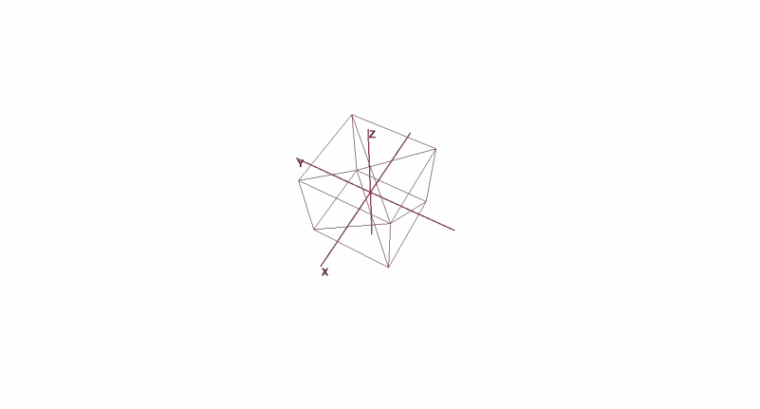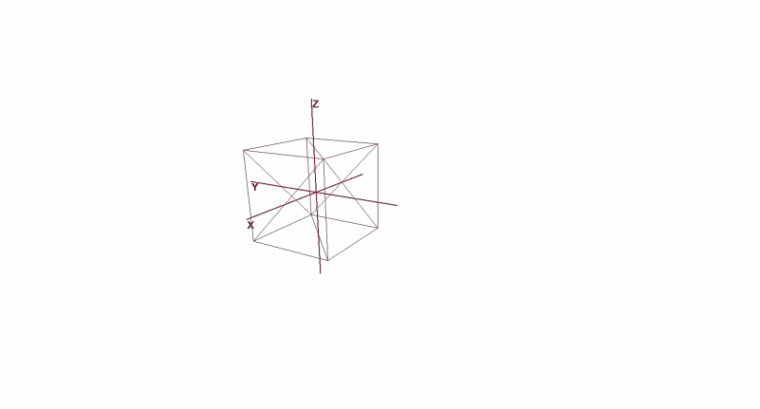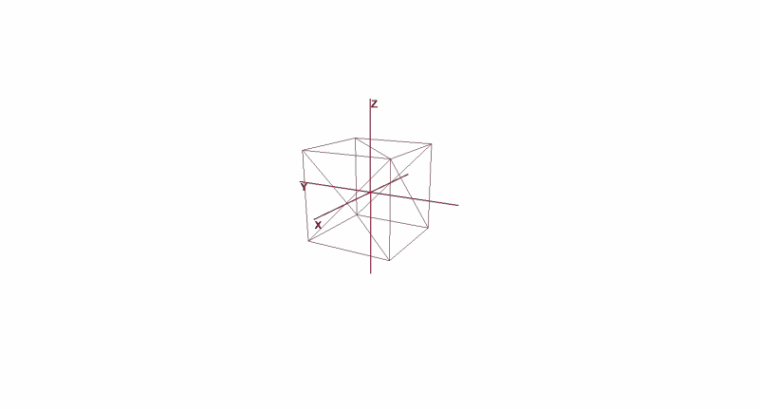
Rotar y mover un objeto usando coordenadas locales

Dibujar polígonos. Cámara

El objeto principal de la escena será la cámara; con la ayuda de ella, los objetos se dibujarán en la pantalla. La cámara, como todos los objetos de la escena, tendrá coordenadas locales en forma de un objeto de la clase Pivot - a través de él moveremos y rotaremos la cámara:





Para mostrar el objeto en la pantalla, usaremos un método de proyección en perspectiva simple . El principio en el que se basa este método es que cuanto más lejos de nosotros esté el objeto, más pequeño parecerá. Probablemente muchos resolvieron alguna vez en la escuela el problema de medir la altura de un árbol a cierta distancia del observador:





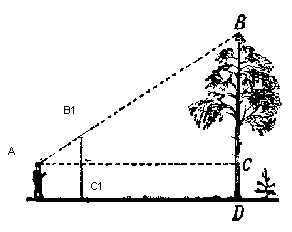
Imagine que un rayo de la parte superior del árbol cae sobre un cierto plano de proyección ubicado a una distancia C1 del observador y dibuja un punto en él. El observador ve este punto y quiere determinar la altura del árbol a partir de él. Como puede ver, la altura del árbol y la altura de un punto en el plano de proyección están relacionadas por la proporción de triángulos similares. Luego, el observador puede determinar la altura del punto usando esta relación:







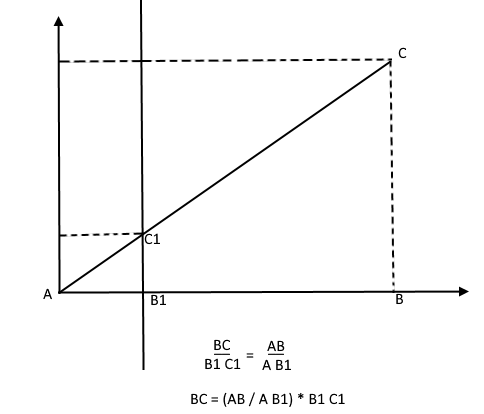
Por el contrario, conociendo la altura del árbol, puede encontrar la altura de un punto en el plano de proyección:







Ahora volvamos a nuestra cámara. Imagine que se adjunta un plano de proyección al eje z de las coordenadas de la cámara a una distancia z ' del origen. La fórmula para tal plano es z = z ' , puede ser dada por un número - z' . Los rayos de los vértices de varios objetos caen en este plano. Cuando el rayo golpea el avión, dejará un punto en él. Al conectar tales puntos, puede dibujar un objeto.







Este plano representará la pantalla. Encontraremos la coordenada de la proyección del vértice del objeto en la pantalla en 2 etapas:

• 1) Traducimos el vértice a las coordenadas locales de la cámara
• 2) Encuentra la proyección de un punto a través de la razón de triángulos similares

La proyección será un vector bidimensional, sus coordenadas x 'e y' definirán la posición del punto en la pantalla de la computadora.





Este código tiene varios errores, de los que hablaremos más adelante.

Cortar polígonos invisibles

Habiendo proyectado tres puntos del polígono en la pantalla de esta manera, obtenemos las coordenadas del triángulo que corresponde a la visualización del polígono en la pantalla. Pero de esta manera la cámara procesará cualquier vértice, incluidos aquellos cuyas proyecciones van más allá del área de la pantalla, si intenta dibujar dicho vértice, existe una alta probabilidad de detectar errores. La cámara también procesará los polígonos que están detrás de ella (las coordenadas z de sus puntos en la base de la cámara local son menores que z ' ); tampoco necesitamos tal visión "occipital".







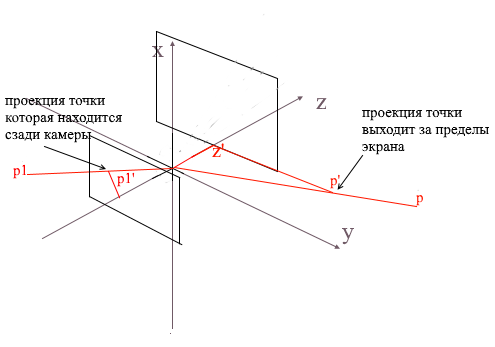
Para recortar vértices invisibles en gl abierto, se utiliza el método de pirámide de truncamiento. Consiste en establecer dos planos: cercano (plano cercano) y lejano (plano lejano). Todo lo que se encuentre entre estos dos planos estará sujeto a un procesamiento adicional. Utilizo una versión simplificada con un plano de recorte: z ' . Todos los vértices detrás de él serán invisibles.



Agreguemos dos nuevos campos a la cámara: ancho y alto de la pantalla.

Ahora comprobaremos cada punto proyectado para ver si toca el área de la pantalla. También cortemos los puntos detrás de la cámara. Si el punto queda atrás o su proyección no cae en la pantalla, entonces el método devolverá el punto {float.NaN, float.NaN} .

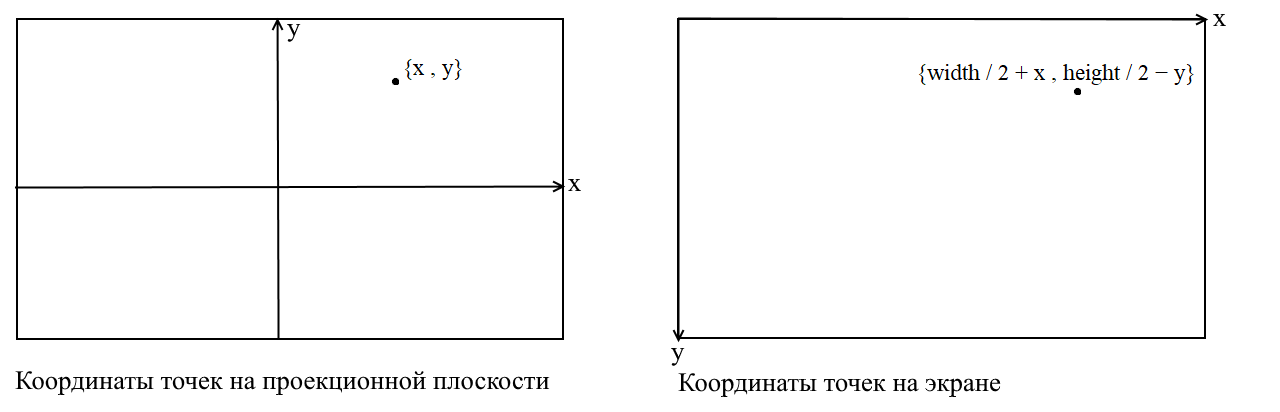
Traducir a coordenadas de pantalla

Aquí aclararé un punto. Está relacionado con el hecho de que en muchas bibliotecas gráficas el dibujo se realiza en el sistema de coordenadas de la pantalla, en tales coordenadas el origen es el punto superior izquierdo de la pantalla, x aumenta cuando se mueve hacia la derecha e y cuando se mueve hacia abajo. En nuestro plano de proyección, los puntos se representan en coordenadas cartesianas ordinarias y, antes de dibujar, estas coordenadas deben convertirse a coordenadas de pantalla. Esto no es difícil de hacer, solo necesita cambiar el origen a la esquina superior izquierda e invertir y :

Ajustar el tamaño de la imagen proyectada

Si usa el código anterior para dibujar un objeto, obtendrá algo como esto:







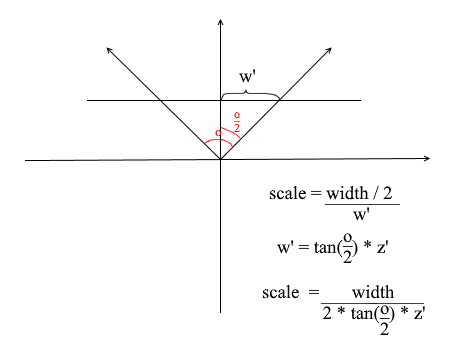
Por alguna razón, todos los objetos se dibujan muy pequeños. Con el fin de entender la razón, recordamos cómo se calculó la proyección - se multiplicó el X y Y coordenadas por el delta del z '/ z relación . Esto significa que el tamaño del objeto en la pantalla depende de la distancia al plano de proyección z ' . Pero podemos establecer z ' tan pequeño como queramos. Por tanto, debemos ajustar el tamaño de la proyección en función del valor z ' actual . Para hacer esto, agreguemos otro campo a la cámara: su ángulo de visión .







Lo necesitamos para hacer coincidir el tamaño angular de la pantalla con su ancho. El ángulo coincidirá con el ancho de la pantalla de esta manera: el ángulo máximo dentro del cual la cámara está mirando es el borde izquierdo o derecho de la pantalla. Entonces, el ángulo máximo desde el eje z de la cámara es o / 2 . La proyección que golpea el borde derecho de la pantalla debe tener la coordenada x = ancho / 2 y la izquierda: x = -ancho / 2 . Sabiendo esto, derivamos la fórmula para encontrar el coeficiente de estiramiento de proyección:









Aquí hay un código de renderizado simple que usé para la prueba:





Revisemos el render en la escena y los cubos:







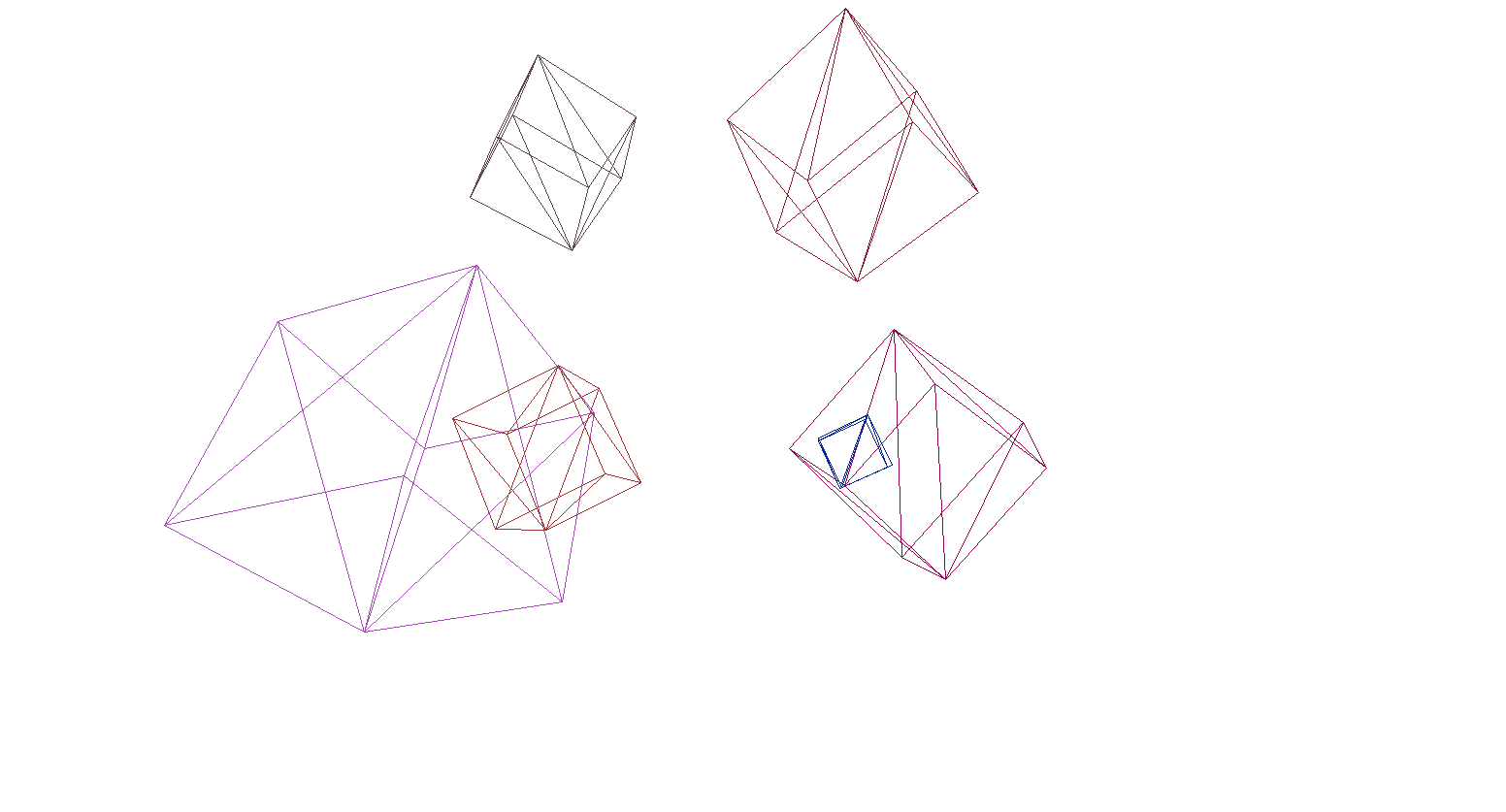
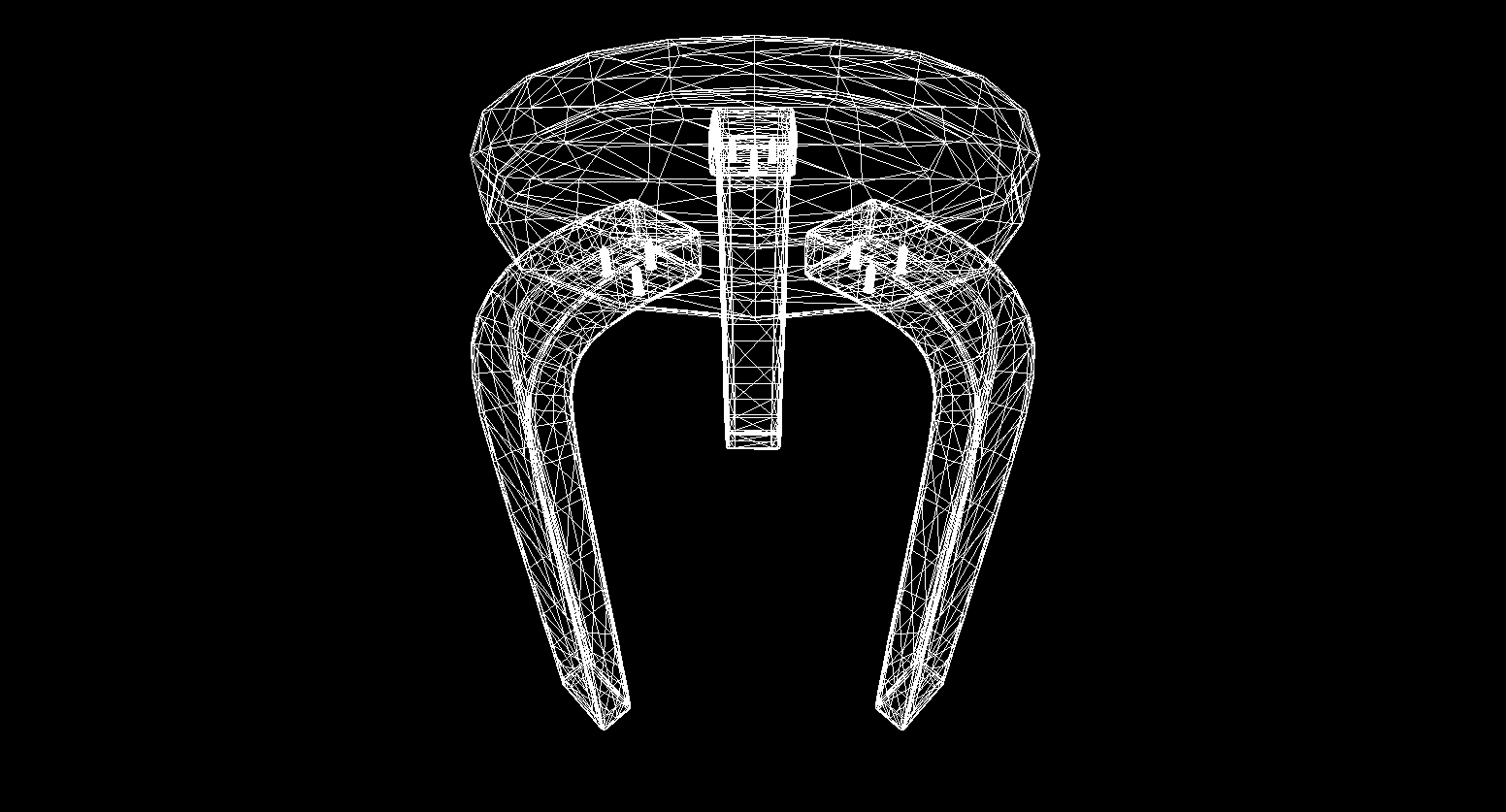
Y sí, todo funciona muy bien. Para aquellos que no encuentran los cubos de colores pretenciosos, escribí una función para analizar modelos de formato OBJ en objetos primitivos, rellené el fondo con negro y rendericé varios modelos:

Rasterización de polígonos. Traemos belleza.

En la última sección, escribimos un render de estructura alámbrica. Ahora nos ocuparemos de su modernización: implementaremos la rasterización de polígonos.



Simplemente rasterizar un polígono significa pintar sobre él. Parecería por qué escribir una bicicleta cuando ya hay funciones de rasterización de triángulos listas para usar. Esto es lo que sucede si dibuja todo con las herramientas predeterminadas:







Se dibujaron arte contemporáneo, polígonos detrás de los frontales, en una palabra: gachas. Además, ¿cómo texturizar objetos de esta manera? Sí, de ninguna manera. ¡Así que tenemos que escribir nuestro propio imba-rasterizador, que podrá cortar puntos invisibles , texturas e incluso sombreadores! Pero para hacer esto, vale la pena comprender cómo pintar triángulos en general.

Algoritmo de Bresenham para dibujo lineal.

Empecemos por las líneas. Si alguien no conocía el algoritmo de Bresenham, este es el algoritmo principal para dibujar líneas rectas en gráficos por computadora. Él o sus modificaciones se usan literalmente en todas partes: dibujar líneas, segmentos, círculos, etc. Cualquier persona interesada en una descripción más detallada, lea la wiki. Algoritmo de Bresenham



Hay un segmento de línea que conecta los puntos {x1, y1} y {x2, y2} . Para dibujar un segmento entre ellos, debe pintar sobre todos los píxeles que caen sobre él. Para dos puntos del segmento, puede encontrar las coordenadas x de los píxeles en los que se encuentran: solo necesita tomar partes enteras de las coordenadas x1 y x2 . Para pintar píxeles en un segmento, comience un ciclo de x1 a x2 y en cada iteración calculey : coordenada del píxel que cae sobre la línea. Aquí está el código:

void Brezenkhem(Vector2 p1 , Vector2 p2)
{
    int x1 = Floor(p1.X);
    int x2 = Floor(p2.X);
    if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
    float d = (p2.Y - p1.Y) / (x2 - x1);
    float y = p1.Y;
    for (int i = x1; i <= x2; i++)
    {
        int pixelY = Floor(y);
        FillPixel(i , pixelY);
        y += d;
    }
}

Imagen de wiki

Rasteriza un triángulo. Algoritmo de relleno

Sabemos trazar líneas, pero con triángulos será un poco más difícil (¡no mucho)! La tarea de dibujar un triángulo se reduce a varias tareas de dibujar líneas. Primero, dividamos el triángulo en dos partes, habiendo ordenado previamente los puntos en orden ascendente x :







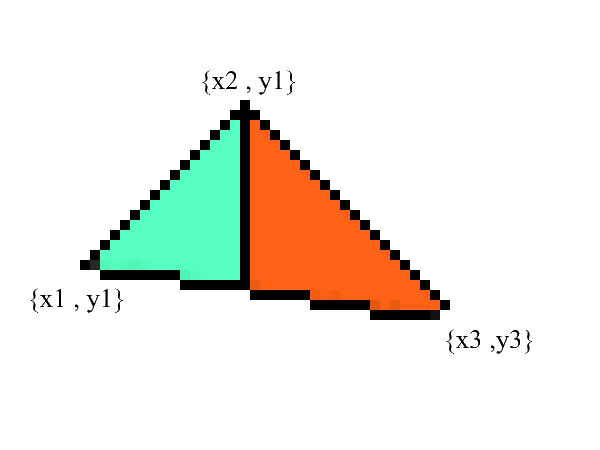
Aviso: ahora tenemos dos partes en las que los bordes superior e inferior están claramente expresados . ¡todo lo que queda es completar todos los píxeles intermedios! Esto se puede hacer en 2 ciclos: de x1 a x2 y de x3 a x2 .

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    // BubbleSort    x
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    //    y    x
    //   0:  x1 == x2     - 
    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;

    //     
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    //     y1
    var up = v1.Y;
    var down = v1.Y;

    for (int i = (int)v1.X; i <= (int)v2.X; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta;
        down += downDelta;
    }

    //       
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);
    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;

    if (upDelta < downDelta) Swap(upDelta, downDelta);

    up = v3.Y;
    down = v3.Y;

    for (int i = (int)v3.X; i >=(int)v2.X; i--)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i, g);
        }
        up += upDelta;
        down += downDelta;
    }
}

Sin duda, este código se puede refactorizar y no duplicar el bucle:

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);

    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);

    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;
    if (upDelta < downDelta) Swap(upDelta, downDelta);

    TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}

void TrianglePart(float x1 , float x2 , float y1  , float upDelta , float downDelta)
{
    float up = y1, down = y1;
    for (int i = (int)x1; i <= (int)x2; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta; down += downDelta;
    }
}

Recortando puntos invisibles.

Primero, piense en cómo ve. Ahora hay una pantalla frente a usted, y lo que está detrás está oculto a sus ojos. En el renderizado, funciona un mecanismo similar: si un polígono se superpone a otro, el render lo dibujará sobre el superpuesto. Por el contrario, no dibujará la parte cerrada del polígono:







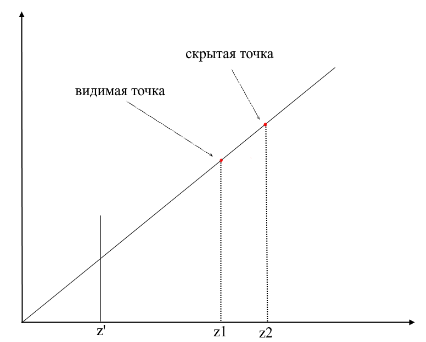
Para comprender si los puntos son visibles o no, se utiliza el mecanismo zbuffer (búfer de profundidad) en el renderizado . zbuffer se puede considerar como una matriz bidimensional (se puede comprimir en unidimensional) con ancho * alto . Para cada píxel de la pantalla, almacena un valor z : las coordenadas en el polígono original desde donde se proyectó este punto. En consecuencia, cuanto más cerca esté el punto del observador, menor será su coordenada z . En última instancia, si las proyecciones de varios puntos coinciden, debe rasterizar el punto con la coordenada z mínima :







Ahora surge la pregunta: ¿cómo encontrar las coordenadas z de puntos en el polígono original? Esto se puede hacer de varias maneras. Por ejemplo, puede disparar un rayo desde el origen de la cámara, pasando por un punto en el plano de proyección {x, y, z '} y encontrar su intersección con el polígono. Pero buscar intersecciones es una operación extremadamente costosa, por lo que usaremos un método diferente. Para dibujar un triángulo, interpolamos las coordenadas de sus proyecciones , ahora, además de esto, también interpolaremos las coordenadas del polígono original . Para cortar puntos invisibles, usaremos el estado zbuffer para el marco actual en el método de rasterización .



Mi zbuffer se verá asíVector3 [] : contendrá no solo coordenadas z , sino también valores interpolados de puntos poligonales (fragmentos) para cada píxel de la pantalla. Esto se hace para ahorrar memoria, ya que en el futuro todavía necesitaremos estos valores para escribir sombreadores . Mientras tanto, tenemos el siguiente código para determinar los vértices visibles (fragmentos) :







Animación de los pasos del rasterizador (al reescribir la profundidad en zbuffer, el píxel se resalta en rojo):



Por conveniencia, moví todo el código a un módulo rasterizador separado:





Ahora revisemos el trabajo de renderizado. Para esto utilizo el modelo de Sylvanas del famoso RPG "WOW":







No muy claro, ¿verdad? Esto se debe a que aquí no hay texturas ni iluminación. Pero lo arreglaremos pronto.

Texturas! ¡Normal! ¡Encendiendo! ¡Motor!

¿Por qué lo combiné todo en una sección? Y porque, en esencia, texturizar y calcular normales son absolutamente idénticos y pronto lo comprenderá.



Primero, veamos el problema de textura de un polígono. Ahora, además de las coordenadas habituales de los vértices del polígono, también almacenaremos sus coordenadas de textura . La coordenada de textura del vértice se representa como un vector 2D y apunta a un píxel en la imagen de textura. Encontré una buena imagen en Internet para mostrar esto:





Tenga en cuenta que el comienzo de la textura ( píxel inferior izquierdo ) en las coordenadas de textura es {0, 0} y el final ( píxel superior derecho ) es {1, 1} . Tenga en cuenta el sistema de coordenadas de textura y la posibilidad de ir más allá de los bordes de la imagen cuando la coordenada de textura es 1.



Creemos una clase para representar los datos del vértice de inmediato:

  public class Vertex
    {
        public Vector3 Position { get; set; }
        public Color Color { get; set; }
        public Vector2 TextureCoord { get; set; }
        public Vector3 Normal { get; set; }

        public Vertex(Vector3 pos , Color color , Vector2 texCoord , Vector3 normal)
        {
            Position = pos;
            Color = color;
            TextureCoord = texCoord;
            Normal = normal;
        }
    }

Explicaré por qué se necesitan las normales más adelante, por ahora solo sabremos que los vértices pueden tenerlas. Ahora, para texturizar el polígono, necesitamos mapear de alguna manera el valor del color de la textura a un píxel específico. ¿Recuerdas cómo interpolamos los vértices? ¡Haz lo mismo aquí! No volveré a escribir el código de rasterización, pero le sugiero que implemente la textura en su renderizado usted mismo. El resultado debe ser la visualización correcta de texturas en el modelo. Esto es lo que tengo:







Toda la información sobre las coordenadas de textura del modelo está en el archivo OBJ. Para usar esto, aprenda el formato: formato OBJ.

Encendiendo

Con las texturas, todo se ha vuelto mucho más divertido, pero será realmente divertido cuando implementemos iluminación para la escena. Para simular una iluminación "barata", utilizaré el modelo Phong .

Modelo Phong

En general, este método simula la presencia de 3 componentes de la iluminación: el fondo (ambiente), disperso (difuso) y espejo (reflejo). La suma de estos tres componentes eventualmente simulará el comportamiento físico de la luz.





Modelo Phong



Para calcular la iluminación Phong necesitamos normales de superficie, para esto las agregué en la clase Vertex. ¿Dónde podemos encontrar los valores de estas normales? No, no necesitamos calcular nada. El hecho es que los generosos editores 3D a menudo los consideran ellos mismos y proporcionan modelos junto con los datos en el contexto del formato OBJ. Habiendo analizado el archivo del modelo, obtenemos el valor normal para 3 vértices de cada polígono.





Imagen de wiki



Para calcular la normal en cada punto del polígono, es necesario interpolar estos valores, ya sabemos cómo hacerlo. Ahora echemos un vistazo a todos los componentes para calcular la iluminación Phong.

Luz de fondo (ambiente)

Inicialmente, configuramos la iluminación de fondo constante , para objetos sin textura, puede elegir cualquier color para objetos con texturas. Divido cada uno de los componentes RGB en una proporción de sombreado básico (baseShading).

Luz difusa

Cuando la luz incide en la superficie del polígono, se dispersa uniformemente. Para calcular el valor difuso en un píxel específico, se tiene en cuenta el ángulo en el que la luz incide en la superficie. Para calcular este ángulo, puede aplicar el producto escalar del rayo incidente y la normal (por supuesto, los vectores deben normalizarse antes de eso). Este ángulo se multiplicará por un factor de intensidad de luz. Si el producto escalar es negativo, significa que el ángulo entre los vectores es mayor de 90 grados. En este caso, comenzaremos a calcular no el aclarado, sino, por el contrario, el sombreado. Vale la pena evitar este punto, puedes hacerlo usando la función max .





Apliquemos luz difusa y disipemos la oscuridad:

Luz de espejo (Reflejar)

Para calcular el componente del espejo, debe tener en cuenta el punto desde el que miramos el objeto . Ahora tomaremos el producto escalar del rayo del observador y el rayo reflejado desde la superficie multiplicado por el factor de intensidad de la luz.





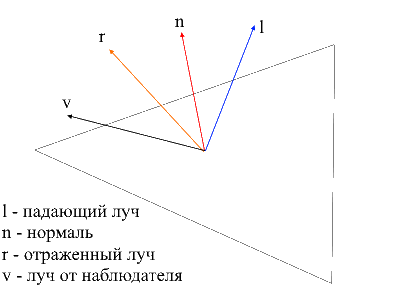
Es fácil encontrar el rayo desde el observador hasta la superficie; simplemente será la posición del vértice procesado en coordenadas locales . Para encontrar el rayo reflejado, utilicé el siguiente método. El rayo incidente se puede descomponer en 2 vectores: su proyección sobre la normal y el segundo vector, que se puede encontrar restando esta proyección del rayo incidente. Para encontrar el rayo reflejado, debe restar el valor del segundo vector de la proyección a la normal.





Ahora la imagen se ve así:

Oscuridad

El punto final de mi presentación será la implementación de sombras para renderizar. La primera idea de callejón sin salida que se originó en mi cráneo es verificar en cada punto si hay algún polígono entre él y la luz . Si es así, no es necesario iluminar el píxel. El modelo de Sylvanas contiene más de 220.000 polígonos. Si es así, para cada punto para verificar la intersección con todos estos polígonos, entonces necesita hacer un máximo de 220,000 * 1920 * 1080 * 219999 llamadas al método de intersección. En 10 minutos, mi computadora pudo dominar la décima parte de todos los cálculos (2600 polígonos de 220,000), después de lo cual tuve un turno y fui en busca de un nuevo método.



En Internet, encontré una forma muy simple y hermosa que realiza los mismos cálculos.miles de veces más rápido . Se llama mapeo de sombras . Recuerde cómo determinamos los puntos visibles para el observador: usamos zbuffer . ¡El mapeo de sombras hace lo mismo! En la primera pasada, nuestra cámara estará en la posición de luz y mirando el objeto. Esto generará un mapa de profundidad para la fuente de luz. El mapa de profundidad es el familiar zbuffer. En la segunda pasada, usamos este mapa para determinar qué vértices deben iluminarse. Ahora romperé las reglas del buen código y seguiré el camino de las trampas: simplemente paso un nuevo objeto rasterizador al sombreador y al usarlo crearé un mapa de profundidad para nosotros.





Para una escena estática, será suficiente llamar a la construcción del mapa de profundidad una vez y luego usarlo en todos los cuadros. Como prueba, estoy usando un modelo menos poligonal de la pistola. Esta es la imagen de salida:







Muchos de ustedes probablemente hayan notado los artefactos de este sombreador (puntos negros no procesados ​​por la luz). Nuevamente, volviendo a la red omnisciente, encontré una descripción de este efecto con el nombre desagradable "acné en las sombras" (perdóneme personas con una apariencia compleja). La esencia de estos "huecos" es que utilizamos la resolución limitada del mapa de profundidad para definir la sombra. Esto significa que varios vértices al renderizar reciben un valor del mapa de profundidad. Los más susceptibles a este artefacto son las superficies sobre las que la luz incide en un ángulo suave . El efecto se puede corregir aumentando la resolución de renderizado de las luces, pero hay una forma más elegante . Consiste en agregarun cambio específico de profundidad en función del ángulo entre el haz de luz y la superficie . Esto se puede hacer usando el producto escalar.

Conclusión

Me considero un principiante en gráficos 3D, no excluyo los errores que cometí en el transcurso de la presentación. Lo único en lo que confío es en el resultado práctico obtenido en el proceso de creación. Puedes dejar todas las correcciones y optimizaciones (si las hay) en los comentarios, estaré encantado de leerlas. Enlace al repositorio del proyecto .