📦 🤴🏼 🚱 Cómo dibujar una estrella (y más) en coordenadas polares 👩🏿‍⚕️ 🚵🏼 👩‍🏭

La cuestión de la fórmula para un polígono en coordenadas polares surge con regularidad en recursos temáticos, y con la misma frecuencia permanece sin una respuesta clara. En el mejor de los casos, se encuentra una solución a través de la función del resto de la división, que no es "limpia" desde un punto de vista matemático, ya que no permite realizar transformaciones analíticas sobre la función. Aparentemente, los verdaderos matemáticos están demasiado ocupados resolviendo problemas del milenio y buscando una prueba simple del teorema de Fermat para prestar atención a problemas tan banales. Afortunadamente, en este asunto, la imaginación es más importante que el conocimiento, y para resolver este problema no es necesario ser profesor de ciencias topológicas, el conocimiento a nivel escolar es suficiente.

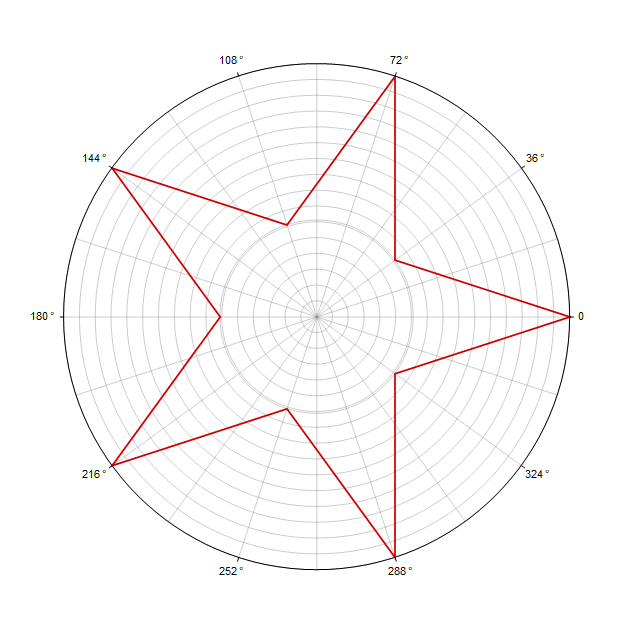
La fórmula para un polígono equilátero en coordenadas polares parece muy simple

ρ = \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n ϕ)) + π m}{2 n})}

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

y tiene los siguientes parámetros:

ϕ

$\phi$ - ángulo;

n

$n$ - el número de vértices convexos;

m

$m$ - determina cuántos vértices estarán los lados en una línea recta. También se permiten valores negativos para él: el signo determinará en qué dirección se doblará la estrella;

k

$k$ - rigidez - en

k = 0

$k=0$ obtenemos un círculo independientemente de otros parámetros, por

k = 1

$k=1$ - un polígono con líneas rectas, en valores intermedios de

0

$0$ antes de

1

$1$ - Figuras intermedias entre un círculo y un polígono.

Con esta fórmula, puede dibujar una estrella de dos formas:

1)

n = 5, m = 3

$n=5, m=3$

n = 5 / 4, m = 0

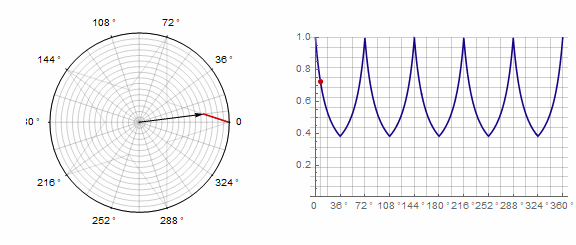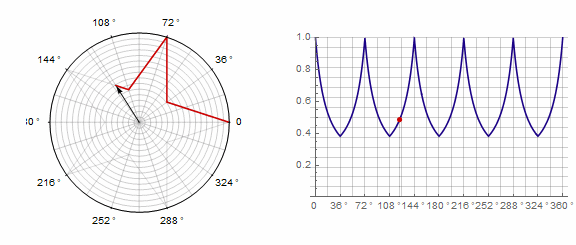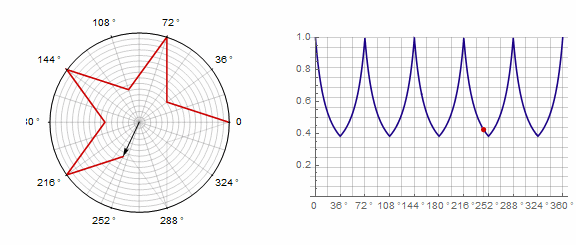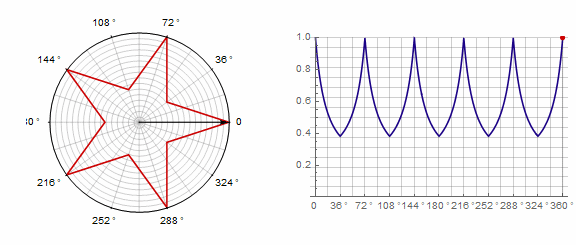
$n=5/4,m=0$ ... En este caso, debe realizar dos vueltas en lugar de una:

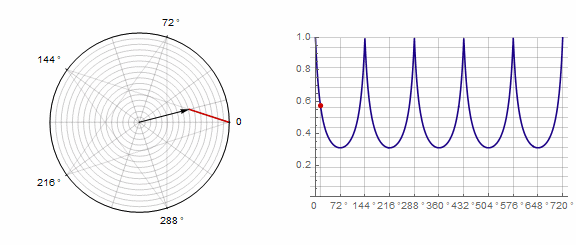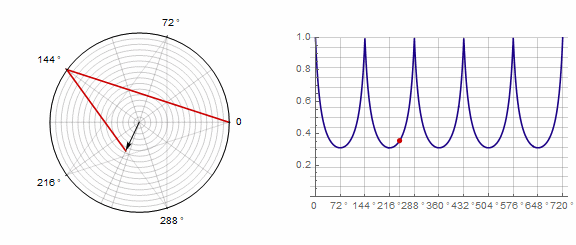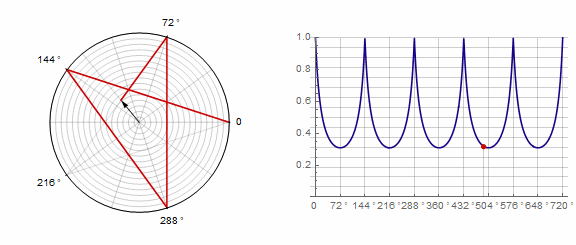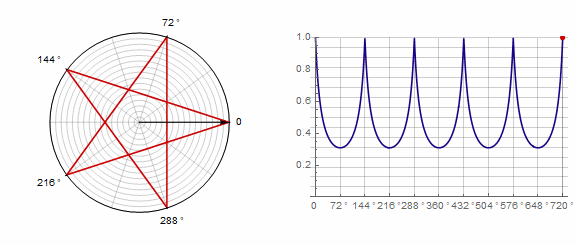
Parámetro

m

$m$ afecta al polígono de la siguiente manera (aquí cambia de -1 a 5):

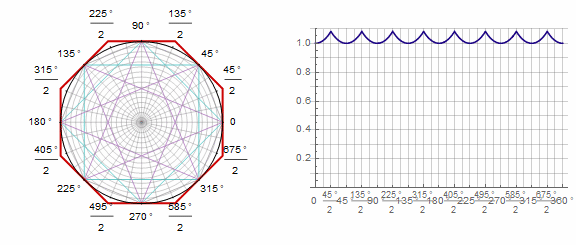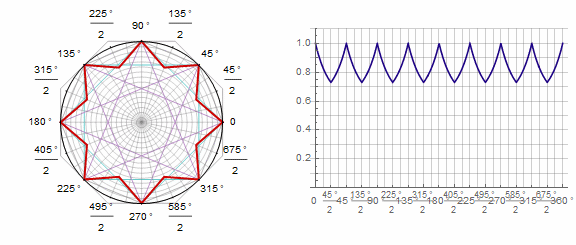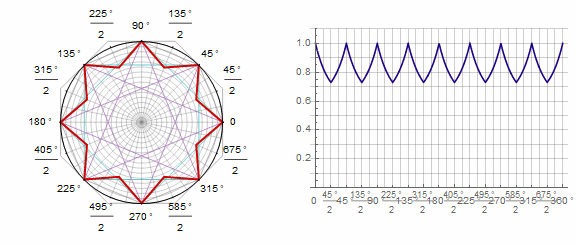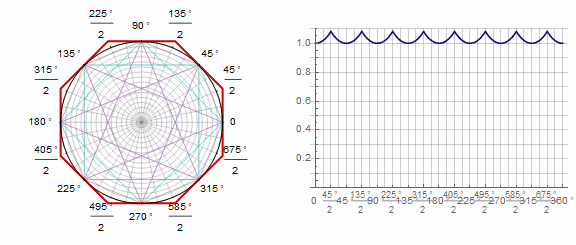
Parámetro

k

$k$ en animación:

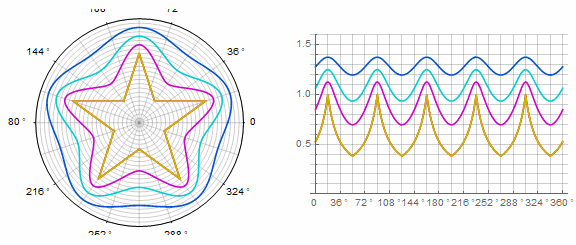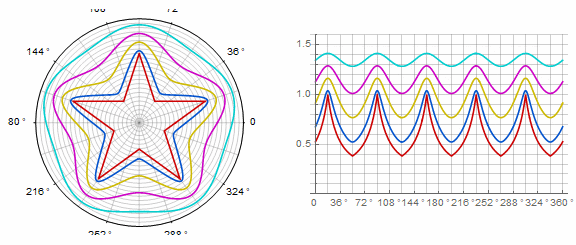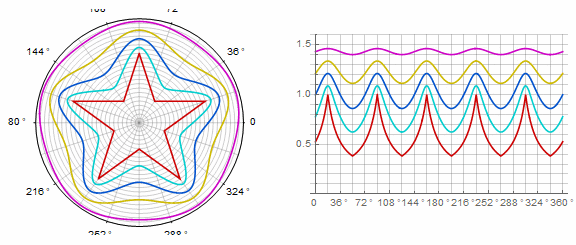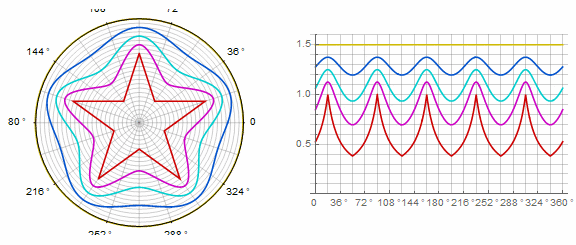
Forma compleja y modificaciones

Puede reescribir la fórmula original en una forma compleja y, a pesar de la presencia de unidades imaginarias en ella, el valor del radio seguirá siendo válido:

ρ = \frac{4^{1 / n} {(\sqrt{1 - k^{2}} + i k)}^{- 1 / n} (1 + {(\sqrt{1 - k^{2}} + i k)}^{2 / n} e^{\frac{i π m}{n}}) {(\sqrt{1 - k^{2} \cos^{2} (n ϕ)} + i k \cos (n ϕ))}^{1 / n}}{4^{1 / n} + e^{\frac{i π m}{n}} {(2 \sqrt{1 - k^{2} \cos^{2} (n ϕ)} + 2 i k \cos (n ϕ))}^{2 / n}}

$\small\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

A primera vista, esto puede parecer inútil, ya que la fórmula se ha vuelto un poco más engorrosa, pero no saque conclusiones precipitadas. En primer lugar, no contiene arcoseno, lo que cambia por completo el significado matemático de la fórmula y le permite ver de manera diferente la construcción de un polígono estrellado. En segundo lugar, también se puede utilizar para obtener fórmulas compactas para casos especiales, por ejemplo

\frac{i^{t} {(i^{n t})}^{1 / n}}{1 + {(i^{n t})}^{2 / n}}

$\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ ... En tercer lugar (y lo más interesante), se puede modificar creativamente y obtener otras formas inesperadas. Para que la aparición de un posible componente imaginario en el radio no provoque ambigüedad en el cálculo, se puede reducir inmediatamente a coordenadas cartesianas multiplicando por

e^{i ϕ}

$e^{i \phi }$ ... A continuación, se muestran ejemplos de algunas de las modificaciones:

\frac{(- 1)^{2 / 3} e^{i ϕ} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{1 / 3}}{(- 1)^{2 / 3} + 2^{2 / 3} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{2 / 3}}

$\frac{(-1)^{2/3} e^{i \phi } \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{1/3}} {(-1)^{2/3}+2^{2/3} \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{2/3}}$

\frac{e^{i ϕ} \sqrt{i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}}}{e^{i / 2} + \sqrt{2} {(i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)})}^{3 / 2}}

$\frac{e^{i \phi } \sqrt{i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}}{e^{i/2}+\sqrt{2} \left(i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}\right)^{3/2}}$

\frac{e^{\frac{1}{4} i (4 ϕ + π)}}{2 \sqrt{(- 1)^{1 / 4} \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}} - 1 - i}

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{(-1)^{1/4} \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}-1-i}$

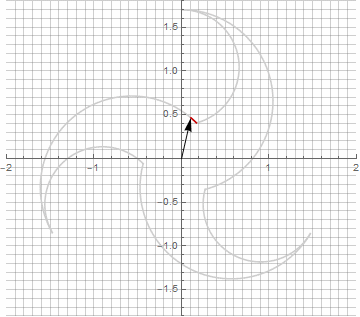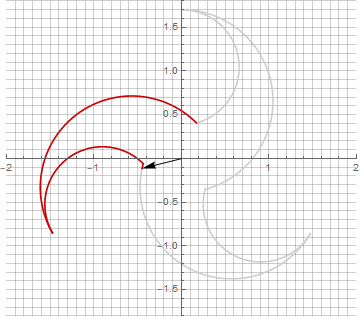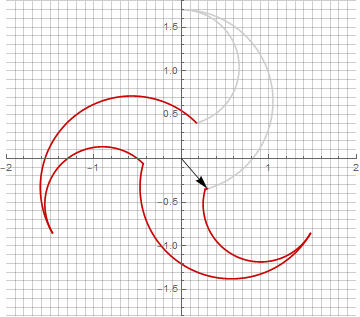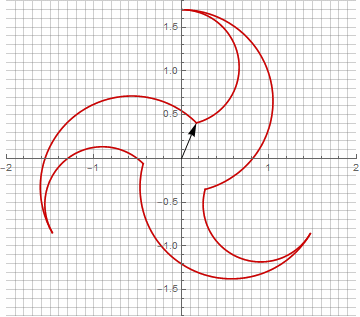
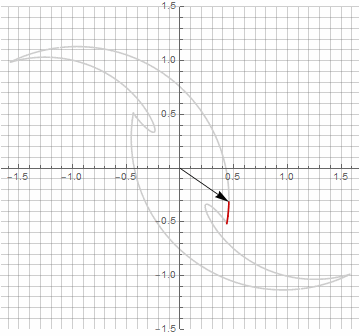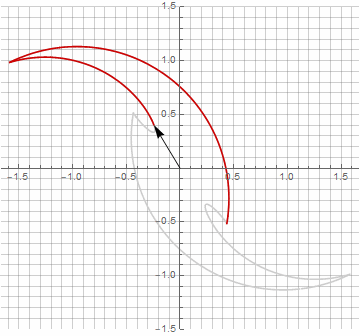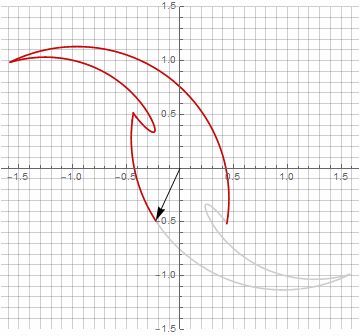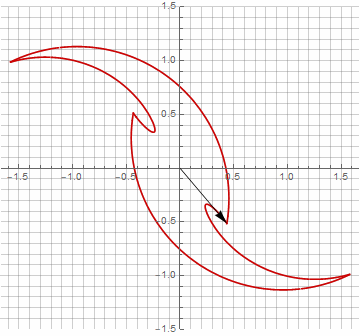
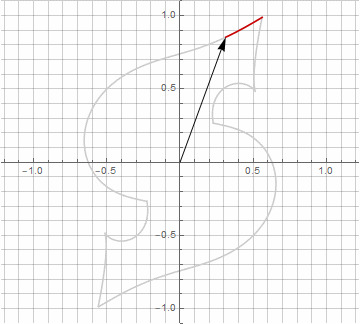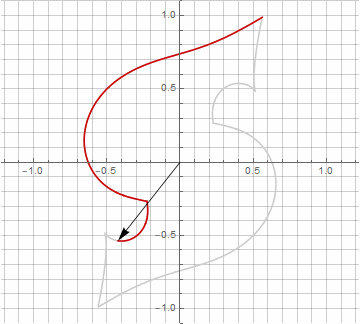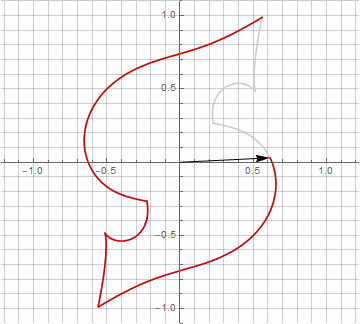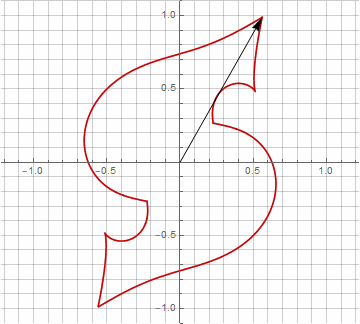
Como probablemente haya notado, la rotación del vector ha dejado de ser uniforme, y precisamente debido a la aparición del componente imaginario en el radio.

Cuadrados y esas cosas

Nuestra fórmula tiene un caso especial maravilloso: un cuadrado, cuya fórmula se puede escribir como

ρ = \frac{2}{\sqrt{2 + \sqrt{2 + 2 \cos (4 ϕ)}}}

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 ϕ)}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

(elige cuál te gusta más).

En un caso un poco más desarrollado, puede definir figuras intermedias entre un círculo y un cuadrado a través de un punto

(k, k)

$(k,k)$ en la superficie

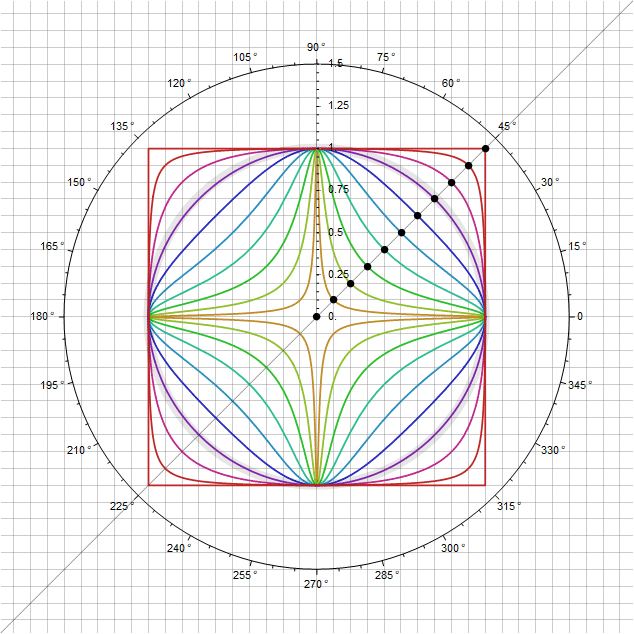
ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \frac{(2 k^{2} - 1) \sin^{2} (2 ϕ)}{k^{4}}}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

También puede agregar variación a estas formas manteniendo la condición de que pasan por el punto

(k, k)

$(k,k)$ - modulando directamente el propio parámetro

k

$k$ dependiendo del ángulo para que al pasar por la diagonal, su multiplicador sea igual a uno. Por ejemplo, sustituyendo en su lugar

k

$k$ función

\frac{k}{1 - z \cos^{2} (2 ϕ)}

$\frac{k}{1-z \cos ^2(2 \phi )}$ , obtendremos un parámetro adicional

z

$z$ con el que se pueden ajustar curvas adicionales. En particular, para

z = 1 / 4

$z=1/4$ obtienes lo siguiente:

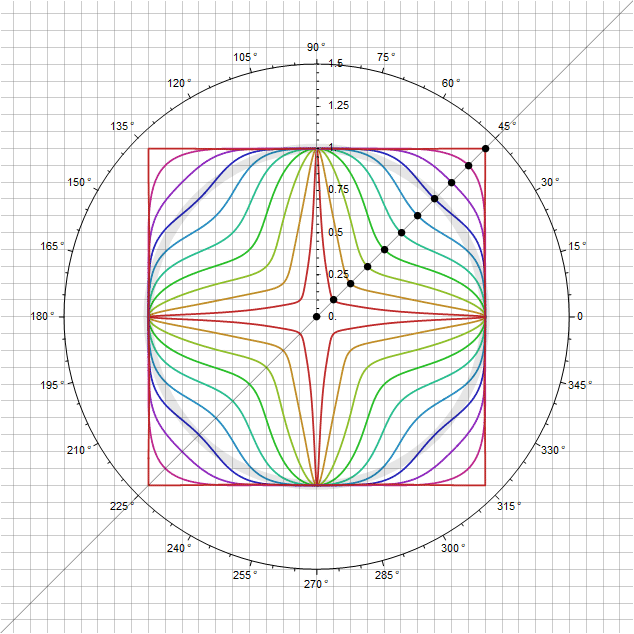
En un caso aún más expandido, puede definir no solo un cuadrado, sino un rectángulo, y aún en coordenadas polares:

ρ = \sqrt{\frac{4 a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (\sqrt{1 - \frac{4 a^{2} b^{2} k \sin^{2} (2 ϕ)}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}} + 1)}}

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

E incluso calcular su área (a través de integrales elípticas):

S = 4 a b \frac{(k - 1) K (k) + E (k)}{k}

$S=4 a b\frac{(k-1) K(k)+E(k)}{k}$

Nota

k

$k$ (

0

$0$

1

$1$ ) ,

π a b

$\pi a b$

4 a b

$4 a b$ .

Esto permitirá realizar perfiles con una transición de un círculo a un rectángulo con un área de sección controlada. Aquí el área es constante:

Y aquí el área se expande exponencialmente:

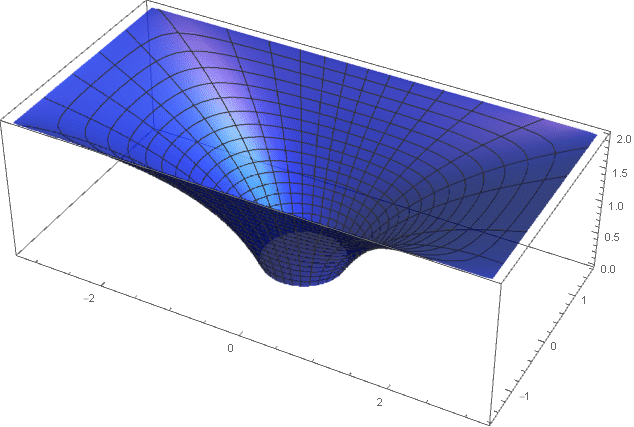
Ir a coordenadas cartesianas

Cualquier fórmula en coordenadas polares se puede expresar a través de una ecuación en coordenadas cartesianas, y al menos de dos maneras, dependiendo de cuál cambie la forma del gradiente en el borde de la figura. Para hacer esto, basta con calcular el ángulo a través de la arcangente de las coordenadas y llevar la fórmula a una constante a través del vector de radio restando

0 = \sqrt{x^{2} + y^{2}} - \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

o división

1 = \frac{\sqrt{x^{2} + y^{2}} \cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

La segunda opción es preferible porque proporciona gradientes rectos a lo largo de los lados del polígono.

Nota

, (0,0) - — , , (

- \cos (\frac{2 \sin^{- 1} (k) + π m}{2 n}) \sec (\frac{2 \sin^{- 1} (k \cos (\frac{π n}{2})) + π m}{2 n})

$-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ ).

\cos (n \tan^{- 1} (x, y))

$\cos \left(n \tan ^{-1}(x,y)\right)$

\frac{(x + i y)^{n} + (x - i y)^{n}}{2 {(x^{2} + y^{2})}^{n / 2}}

$\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , A034839.

El valor de la fórmula del lado derecho de la ecuación (en el segundo caso) cambiará de

0

$0$ antes de

1

$1$ si punto

(x, y)

$(x,y)$ entra en la figura, y desde

1

$1$ ad infinitum - si no. Al elegir diferentes funciones para convertirlo en brillo, puede obtener diferentes opciones de rasterización. Para el exponente (

e^{- x - 1}

$e^{-x-1}$ por el primero y

e^{- x}

$e^{-x}$ para la segunda opción) obtenemos

o, si con saturación

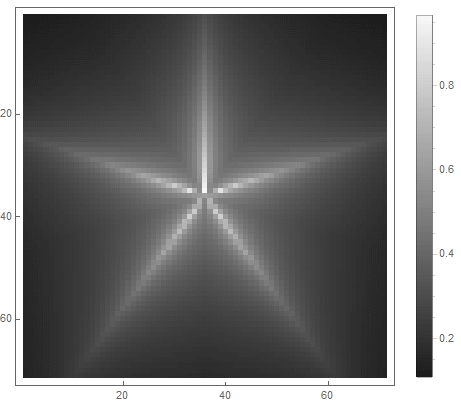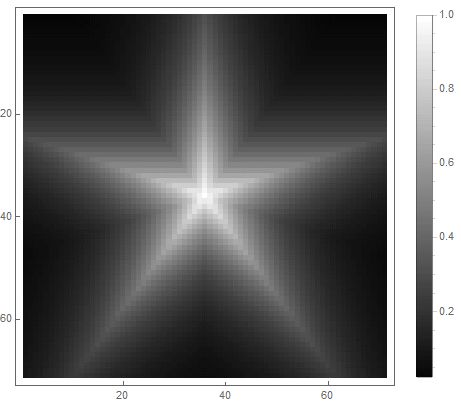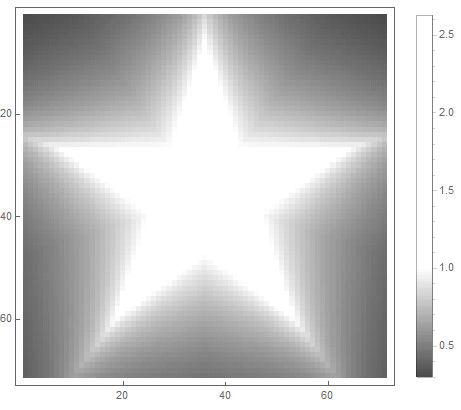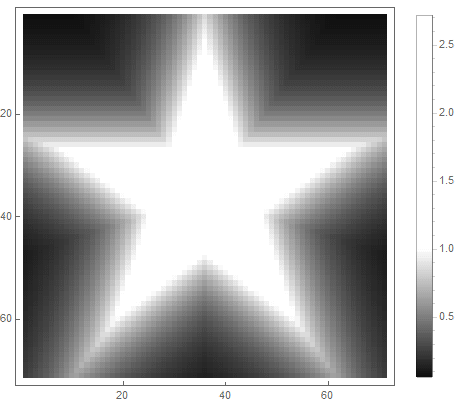Se puede utilizar un filtro de paso bajo clásico

\frac{1}{1 + x^{p}}

$\frac{1}{1+x^p}$ , en el cual

p

$p$ - el orden del filtro, que determina el grado de atenuación.

Para la primera opción:

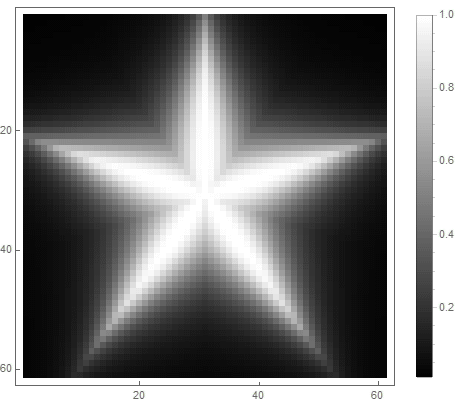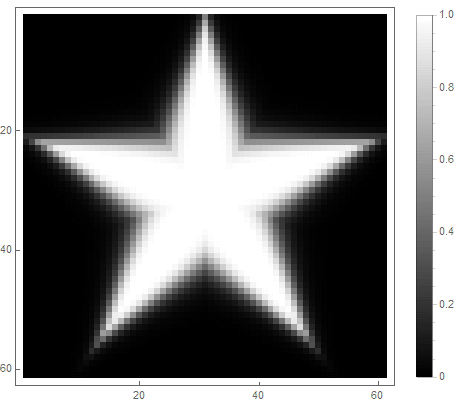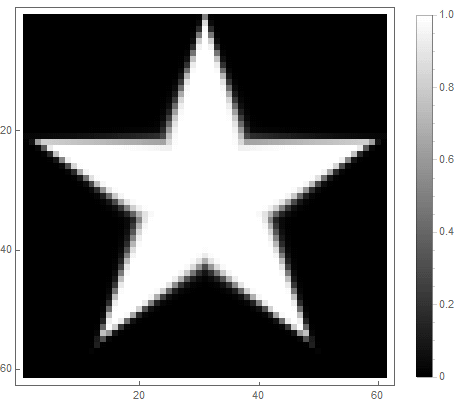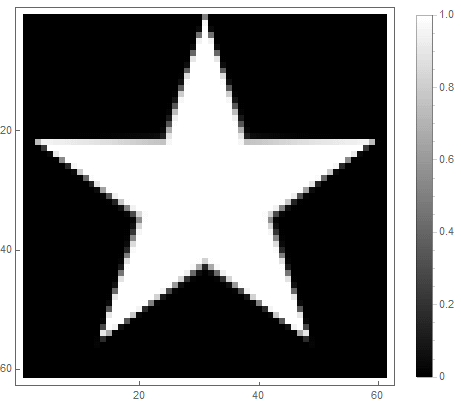Y para el segundo:

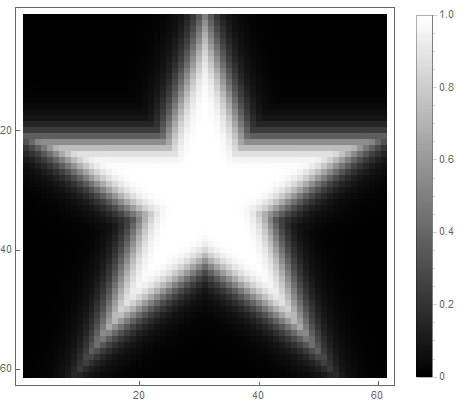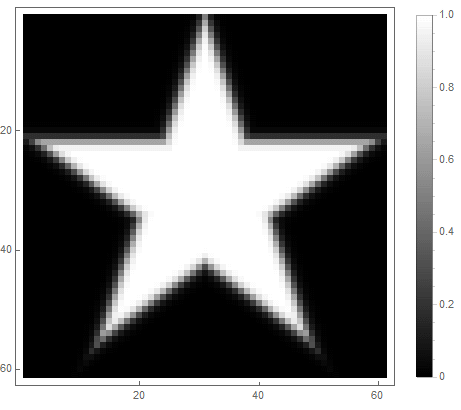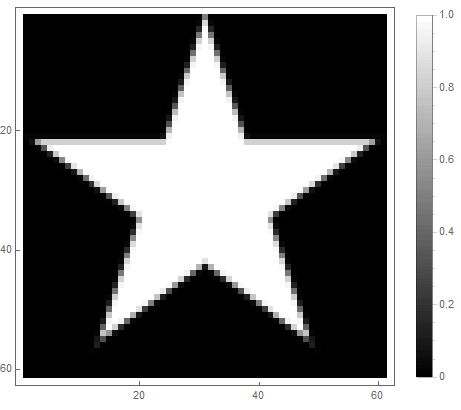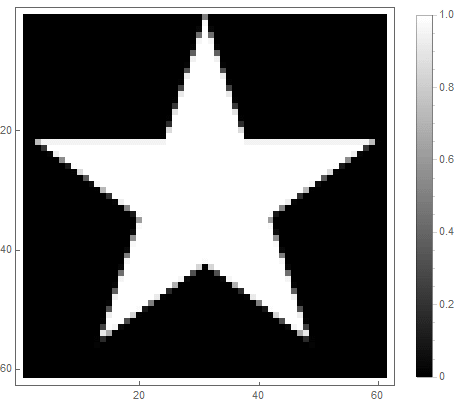También puede utilizar una función continua por partes estableciendo explícitamente los límites de interpolación.

Además de la rasterización como tal, también puede establecer deformaciones, por ejemplo, comprimir el tablero de ajedrez en un círculo:

O incluso póngalo sobre una esfera:

Fórmula

x = \frac{u}{\sqrt{\frac{2}{1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$x=\frac{u}{\sqrt{\frac{2}{1+ \left| \frac{u^2-v^2}{u^2+v^2} \right|}}}$

y = \frac{v}{\sqrt{1 + \frac{2}{| \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$y=\frac{v}{\sqrt{1+\frac{2}{\left| \frac{u^2-v^2}{u^2+v^2}\right| }}}$

z = \sqrt{1 - \frac{1}{2} u^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |) - \frac{1}{2} v^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |)}

$z=\sqrt{1-\frac{1}{2} u^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)-\frac{1}{2} v^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)}$

Apéndice: cómo se derivó la fórmula

El estilo clásico de contar historias en los textos matemáticos consiste en la alternancia de lemas / teoremas y sus demostraciones, como si los enunciados demostrables aparecieran en la cabeza de los autores por una revelación desde arriba. Y aunque hay algo de verdad en esto, más a menudo la aparición de fórmulas va precedida de algún trabajo de investigación, cuya descripción puede dar una mayor comprensión de su significado que la prueba formal; y la fidelidad de las declaraciones, a su vez, se puede rastrear a través de la fidelidad de los pasos que condujeron a ellas.

Así que aquí también: si el artículo comenzara con una fórmula en una forma compleja, entonces su apariencia no sería obvia y contraria a la intuición, y las propiedades declaradas requerirían pruebas adicionales. Pero en la forma trigonométrica de registro, es bastante posible rastrear la historia de su aparición.

1) comenzamos con el caso más simple: la tarea de dibujar una línea recta en coordenadas polares. Para hacer esto, necesitas resolver la ecuación

r \cos (ϕ) = 1

$r \cos (\phi )=1$ cuya solución es obvia

r \to \sec (ϕ)

$r\to \sec (\phi )$ ...

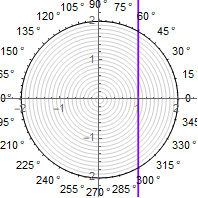
2) además, el argumento de la secante necesita ser "enlazado" para proporcionar torceduras en línea recta. Es en esta etapa cuando otras soluciones utilizan un "truco sucio" en forma de resto de división. También usa la toma secuencial de la función seno directa e inversa -

\sin^{- 1} (\sin (ϕ))

$\sin ^{-1}(\sin (\phi ))$

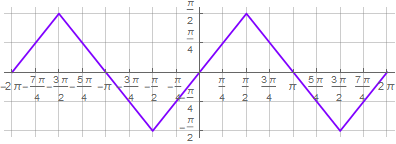
Este enfoque le permite realizar operaciones matemáticas estándar en la fórmula resultante,

p.ej

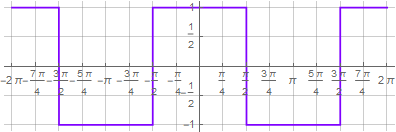
\frac{\partial \sin^{- 1} (\sin (ϕ))}{\partial ϕ} = \frac{\cos (ϕ)}{\sqrt{1 - \sin^{2} (ϕ)}}

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

Gracias a la misma notación, puede simplificar la función cuadrada en coordenadas polares a un aspecto más estético, utilizando la representación compleja de funciones trigonométricas. En Wolfram Mathematica, esto se puede hacer usando las funciones TrigToExp y ExpToTrig:

El código

Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify

↓

\frac{2}{\sqrt{2 + 2 \sqrt{1 - k^{2} \sin^{2} (2 ϕ)}}}

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

Gracias a la misma grabación, puede obtener figuras intermedias suaves entre un círculo y un cuadrado usando un multiplicador adicional

k

$k$ debido a que el argumento de arcoseno no llega a uno -

\sin^{- 1} (k \sin (ϕ))

$\sin ^{-1}(k \sin (\phi ))$ :

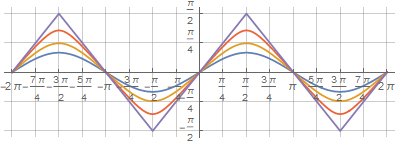
Y para que la función intersecte un punto dado, solo necesita hacer una ecuación y volver a calcular

k

$k$ :

\sqrt{\frac{2}{1 + \sqrt{1 - k^{'} \sin^{2} (\frac{π}{2})}}} = k

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

El código

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k

↓

k^{'} \to \frac{4 (k^{2} - 1)}{k^{4}}

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3) parámetros

n

$n$ y

m

$m$ simplemente se agregaron de una manera creativa y sus efectos se investigaron experimentalmente, de hecho.

4) El rectángulo es fácil de obtener yendo a la vista paramétrica y "estirando" los ejes.

x = a \cos (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

y = b \sin (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

Pero después de eso

t

$t$ ya no significará ángulo, ahora

t

$t$ Es solo un parámetro que describe un vector a través de sus proyecciones sobre los ejes de coordenadas. Para volver a las coordenadas polares, necesitas encontrar la longitud del vector (a través de la raíz de la suma de cuadrados), el ángulo (a través de la arcangente de la razón), expresar este ángulo mediante

ϕ

$\phi$ y sustituya la expresión resultante en su lugar

t

$t$ ...

El código

With[{r = Sqrt[2/(1 + Sqrt[
      

        
        
        
      

    
 1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2], 
      

        
        
        
      

    
 ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

↓

{\sqrt{2} \sqrt{\frac{a^{2} \cos^{2} (t) + b^{2} \sin^{2} (t)}{\sqrt{\cos^{2} (2 t)} + 1}}, \tan^{- 1} (\frac{b \tan (t)}{a})}

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]

↓

t \to \tan^{- 1} (\frac{a \tan (ϕ)}{b})

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])]
      

        
        
        
      

    
/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify

↓

\sqrt{2} \sqrt{\frac{a^{2} b^{2} \sec^{2} (ϕ)}{(a^{2} \tan^{2} (ϕ) + b^{2}) (\sqrt{\cos^{2} (2 \tan^{- 1} (\frac{a \tan (ϕ)}{b}))} + 1)}}

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

Simplificar tal fórmula ya es más difícil, y esto requerirá varias etapas:

ir a las coordenadas cartesianas reemplazando $\phi \to \tan ^{-1}(x,y)$ ;
ir a la forma exponencial;
simplificar;
hacer un reemplazo inverso $x\to \cos (\phi )$ y $y\to \sin (\phi )$ ;
volver a la forma exponencial;
simplificar.

Como resultado, obtenemos la siguiente fórmula:

El código

Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) /
      

        
        
        
      

    
((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])
      

        
        
        
      

    
(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y] 
      

        
        
        
      

    
// TrigToExp // Simplify 
      

        
        
        
      

    
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} & 
      

        
        
        
      

    
// TrigToExp // Simplify // FullSimplify

↓

2 \sqrt{\frac{a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (1 + \sqrt{\frac{{((a^{2} + b^{2}) \cos (2 ϕ) - a^{2} + b^{2})}^{2}}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}})}}

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

Conclusión

Como puede ver, incluso en algo tan simple y común como un polígono, puede encontrar y crear algo nuevo. Y la historia no termina ahí: la fórmula del área para el caso general permaneció desconocida, la fórmula para un polígono arbitrario, y no solo regular, permaneció desconocida, y la expansión en potencia y series trigonométricas se dejó sin consideración. También, probablemente, existe un tipo similar de fórmula para el caso tridimensional.

Por lo tanto, si le dicen que todo en matemáticas ya se ha inventado y solo hay problemas que están más allá de la comprensión de una persona común, no lo crea. Hay muchos problemas puramente prácticos de los que los matemáticos reales no son conscientes, o no están interesados en su solución debido a la falta de publicidad suficiente a su alrededor, o porque ya tienen una idea aproximada de las formas de lograrlos para su solución. No tenga miedo de abordar problemas cuyas soluciones no están disponibles en Wikipedia, no tenga miedo de publicar sus soluciones y no tenga miedo de leer los comentarios debajo de los artículos sobre la inutilidad de todo.

PD descargue el documento original de Mathematica aquí .

Cómo dibujar una estrella (y más) en coordenadas polares

Forma compleja y modificaciones

Cuadrados y esas cosas

Ir a coordenadas cartesianas

Apéndice: cómo se derivó la fórmula

Conclusión

More articles: