👋🏽 👌🏾 👍🏽 Tomando decisiones. Ejemplo 🤶🏿 💛 🍮

Otros artículos del ciclo

Toma de decisiones

Toma de decisiones. Ejemplo

Continuando con el tema, diré que miré las publicaciones de otros autores de Habr sobre este tema. Hay interés en los problemas, pero nadie quiere meterse en la teoría. Actuando como descubridores pioneros. Sería genial si recibieran nuevos resultados, logros, pero nadie se esfuerza por lograrlo.

Pero en realidad resulta peor de lo que ya se sabe, no se tienen en cuenta muchos factores, se aplican los resultados de la teoría donde no se recomienda hacerlo y en general no todo parece muy serio, aunque Habr, como debe entenderse, no se esfuerza por ello. Los lectores no pueden ni deben actuar como un filtro.

El conjunto original de alternativas, su medición y evaluación.

Se sabe que los problemas de encontrar una solución surgen solo en situaciones de elección con múltiples alternativas. Para considerar la situación de toma de decisiones, formular un problema específico de toma de decisiones (DP), elegir un método para resolverlo, es necesario tener alguna información inicial sobre alternativas, una relación de preferencia.

Demostremos en la subsección qué métodos existen para obtenerlo. Las alternativas tienen muchas propiedades (características) que influyen en la decisión. Por ejemplo, los indicadores de propiedades de los objetos (peso, volumen, dureza, temperatura, etc.) pueden ser cuantitativos o cualitativos.

Sea alguna propiedad del conjunto de alternativas de Ω expresada por un número, es decir, existe un mapeo ψ: Ω → E1, donde E1 es el conjunto de números reales. Entonces, dicha propiedad se caracteriza por un indicador, y el número z = ψ (x) se denomina valor (estimación) de la alternativa en términos del indicador.

Para evaluar alternativas, es necesario medir los indicadores.

Definición. La medición de un indicador de una determinada propiedad se entiende como la asignación de valores numéricos a niveles individuales de este indicador en determinadas unidades. En este caso, la elección de la unidad de medida es importante.

Entonces, por ejemplo, si el volumen de una cierta parte del contenedor se mide primero en metros cúbicos y luego en litros, entonces la esencia del indicador no cambiará; solo cambiará el número de unidades. Estas métricas de propiedad se pueden escalar, multiplicar o dividir por un valor constante para la métrica de propiedad.

Por otro lado, existen propiedades cuyos indicadores no permiten tal manipulación de sus valores. El grado de calentamiento de los cuerpos se caracteriza por la temperatura y se mide en grados. El valor de este indicador + 10 ° y –15 ° no permite juzgar cuántas veces el cuerpo con una temperatura de + 10 ° se calienta más que un cuerpo con una temperatura de –15 °

A partir de estos ejemplos, es posible (e importante) concluir que los índices volumen y temperatura se refieren a diferentes tipos de propiedades, sobre los valores de z = ψ (x) de las cuales ciertas transformaciones f (z) = f (ψ (x)) son admisibles o no permitidas ...

Es decir, el conjunto de transformaciones admisibles f (z) se toma como base para determinar el tipo de escala en la que se mide el indicador de un determinado atributo (propiedad). Realizando una u otra medida del indicador de una característica que destaca el investigador, llegamos a la tarea de determinar el tipo de escala en la que se debe realizar la medida.

Sin resolver este problema correctamente, podemos admitir un manejo incorrecto de los resultados de las observaciones (medidas) al procesarlas. Esto sucede cuando los valores de los indicadores sufren transformaciones tomadas fuera del conjunto de transformaciones permitidas para un tipo de escala determinado.

Definición. Una escala de medición es una secuencia de valores de los mismos valores de varios tamaños aceptados de común acuerdo.

Consideremos con más detalle los principales tipos de escalas.

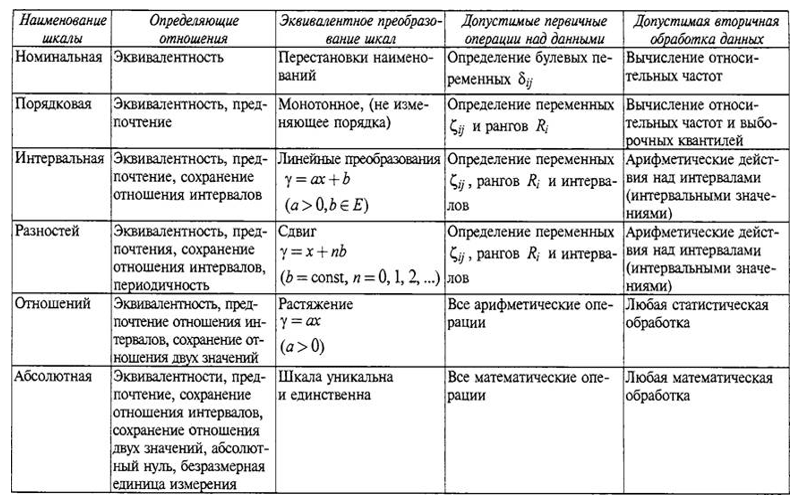
1. Escalas nominales . Las escalas nominales se utilizan cuando un investigador trata con objetos descritos por algunas características. Dependiendo de si un objeto dado tiene un cierto valor de una característica o su ausencia, el objeto se refiere a una u otra clase.

Por ejemplo, si hablamos de personas, entonces el valor de la característica (la escala de la característica está formada por dos valores de sexo: masculino y femenino) le permite asignar inequívocamente a cada persona a una determinada clase. Por esta razón, la escala se llama escala de calificación. Tal signo como profesión permite que una persona sea llamada, por ejemplo, maestro, carpintero o de alguna otra manera de acuerdo con el valor del indicador de una profesión.

La escala en este caso está formada por los nombres de todas las profesiones. Evidentemente, el cero no se indica en esta escala, aunque la ausencia de profesión en la asignatura permite que se le asigne precisamente a la categoría de personas sin profesión. Los nombres de las profesiones no están ordenados de ninguna manera en esta escala, aunque a menudo se ordenan alfabéticamente por razones de conveniencia.

A partir de estas consideraciones, dicha escala se denomina escala de denominación.

Las transformaciones válidas de valores en esta escala son todas funciones uno a uno: f (x) ≠ f (y) <=> x ≠ y.

2. Escalas ordinales . Si el rasgo estudiado, por ejemplo, la dureza del material, se manifiesta de manera diferente en los objetos y tiene valores que no se pueden medir específicamente, pero uno puede juzgar inequívocamente la intensidad comparativa de su manifestación para dos objetos cualesquiera, entonces dicen que el valor del rasgo se mide en una escala ordinal. Un ejemplo clásico de esto es la dureza de los minerales. El punto de referencia es 0 en la escala no definida.

El valor característico se define como sigue. El mineral más duro del par en cuestión deja un rasguño en el otro. Todos los minerales de acuerdo con los valores de este rasgo se pueden ordenar de la siguiente manera: el primero es el menos duro, el segundo es más duro, deja un rasguño solo en el primero, el tercero deja un rasguño en los dos primeros, etc.

La diferencia entre la escala ordinal y el nominal es que los valores del rasgo se pueden clasificar, mientras que los valores en la escala nominal ni siquiera se pueden ordenar. La desventaja de una escala ordinal es que no es proporcional.

Es imposible responder a la pregunta de cuánto o cuántas veces un mineral es más duro que otro. Las transformaciones admisibles de la escala ordinal consisten en todas las funciones monotónicamente crecientes con la propiedad: x ≥ y => f (x) ≥ f (y).

3.Escala de intervalo (intervalo). difieren de las escalas de orden en que para las propiedades que describen, tiene sentido no solo la equivalencia y las relaciones de orden, sino también la suma de intervalos (diferencias) entre varias manifestaciones cuantitativas de propiedades. Un ejemplo típico es la escala de intervalo de tiempo.

Los intervalos de tiempo (por ejemplo, períodos de trabajo, períodos de estudio) se pueden sumar y restar, pero no tiene sentido agregar las fechas de cualquier evento.

Otro ejemplo, la escala de longitudes (distancias): los intervalos espaciales se determina alineando el cero de la regla con un punto, y la lectura se realiza en otro punto. Este tipo de escala también incluye las escalas de temperatura Celsius, Fahrenheit, Reaumur.

Las transformaciones lineales son admisibles en estas escalas, (x - y) / (z -v); x ∓ y; aplican procedimientos para encontrar la expectativa matemática, la desviación estándar, el coeficiente de asimetría y los momentos de compensación.

4. Escala de diferencias (punto) Las escalas de diferencias difieren de las escalas de orden en que la escala de intervalos ya se puede juzgar no solo que el tamaño es mayor que otro, sino también cuánto más, en esencia, esta es la misma escala absoluta, pero sus valores están desplazados por algún valor relativo a los valores absolutos (x - y) <(z -v); x ∓ y;

5. Escala de relaciones... La escala para la cual el conjunto de transformaciones admisibles consta de todas las transformaciones de similitud se llama escala de relaciones. El punto de referencia se fija en esta escala y la escala de medición se puede cambiar para él.

Deje que esta escala mida la longitud de un objeto. En este caso, puede pasar de medir en metros a medir en centímetros, reduciendo la unidad de medida en un factor de 100. Obviamente, en este caso, la relación de las longitudes L (A) y L (B) de dos objetos A y B, medidos en las mismas unidades, no cambiará cuando se cambien las unidades.

Los valores del indicador del rasgo, medidos en esta escala, permiten

responder a la pregunta de cuántas veces más intensamente se manifiesta el rasgo en un objeto que en otro. Para ello, es necesario considerar la relación de los valores L (A) / L (B) = k.

Si la relación es mayor que uno (k> 1), el valor del indicador de atributo para el primer objeto A es k veces mayor que el de B, si k <1, entonces el valor del indicador de atributo para el objeto B es 1 / k veces mayor que el de A. es la multiplicación por un entero positivo y solo eso.

6. Escala absoluta . La más simple de todas las escalas es una escala que permite solo una transformación f (x) = x. Esta situación corresponde a la única forma de medir el indicador de la propiedad de un objeto, a saber, un simple recuento de objetos.

Esta escala se llama escala absoluta. Cuando registramos el objeto x, no nos interesa nada más que este objeto. La escala absoluta puede considerarse como una implementación particular de algunas otras escalas.

Tarea de toma de decisiones. Obteniendo una matriz de relaciones

Enumeramos las posibles configuraciones del ZPR, estas incluyen:

ordenamiento lineal de alternativas (la parte superior de la cadena es la mejor);
destacando la mejor alternativa;
destacando un subconjunto (desordenado) de las mejores alternativas;
destacando un subconjunto ordenado de las mejores alternativas;
ordenamiento parcial de alternativas;
división ordenada (parcialmente ordenada) de alternativas;
partición desordenada de alternativas (clasificación).

A partir del análisis de mediciones de indicadores de propiedades de alternativas en diferentes escalas, los resultados de la medición pueden presentarse de diferentes formas [1, 5].

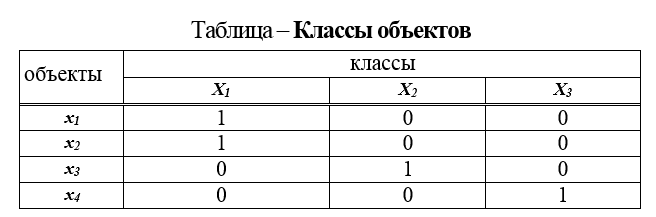
1. Tabla de clasificación. La tabla se obtiene cuando las medidas se toman en escalas nominales y es una tabla, cuyas filas son: el nombre del objeto, y las columnas son los nombres de las clases.

X_{1}, X_{2}, X_{3},

$X_1, X_2, X_3,$ ... y así sucesivamente En las columnas clase 1, clase 2, etc., se establece 1 si el objeto pertenece a esta clase y 0, si no (Clases de tabla de objetos).

En la tabla de clases, objetos

x_{1}, x_{2} є X_{1}, x_{3} є X_{2}, x_{4} є X_{3} .

$x_1 ,x_2 є X_1, x_3 є X_2, x_4 є X_3.$

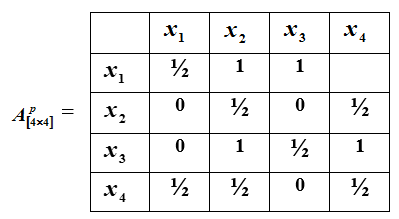
2. Matriz de la relación de preferencias. Se obtiene tomando medidas en escalas ordinales. Revelar preferencias sobre el conjunto de objetos Ω significa indicar el conjunto de todos esos pares de objetos (x, y) de este conjunto para los que el objeto x es preferible (por ejemplo, más duro) que el objeto y. La matriz de relaciones de preferencias se obtiene como sigue. ( ver aquí, fig 2.15 )

En construcción

А_{[n \times n]}^{p}

$_{[n×n]}^p$ matriz cuadrada. Su i-ésima línea corresponde al i-ésimo elemento

x_{i}

$x_i$ del conjunto Ω, y la j-ésima columna al elemento

x_{j}

$x_j$ ... En la intersección de la i-ésima fila y la j-ésima columna, se pone 1 si el objeto

x_{i}

$x_i$ preferido sobre el objeto

x_{j}

$x_j$ , cero si el objeto

x_{j}

$x_j$ preferido sobre el objeto

x_{i}

$x_i$ , 1/2 si objetos

x_{i}

$x_i$ y

x_{j}

$x_j$ indiferente, y no se pone nada - si los objetos son incomparables

x_{i}

$x_i$ y

x_{j}

$x_j$ no se puede comparar.

En la siguiente matriz se presenta un ejemplo de tal relación de preferencia.

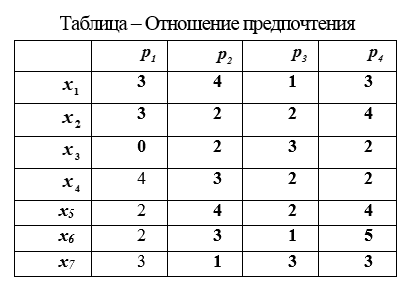
3. Cuadro de indicadores. Se obtiene al medir en la escala de relaciones. Se seleccionan las propiedades de los indicadores que se medirán. Se realiza la medición de estas propiedades y los resultados de la medición se registran en una tabla.

En columnas

p_{1}, p_{2}, p_{3}, p_{4}

$p_1, p_2, p_3, p_4$ Las tablas de razón de preferencia contienen valores de indicadores de propiedad mediante los cuales se evalúan los objetos

x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}

$x_1,x_2,x_3,x_4,x_5,x_6$ y

x_{7}

$x_7$ ...

Después de recibir los resultados de la medición en estas formas de presentación, necesitamos mostrar los resultados en forma de relaciones, ya que resolveremos la ZPR, apoyándonos en el aparato bien desarrollado de la teoría de relaciones binarias.

El mapeo de la tabla de preferencias a la matriz de relaciones binarias es el siguiente:

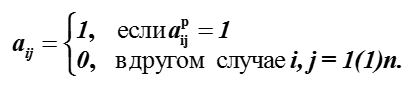
De la matriz de relaciones de preferencias

А_{[4 \times 4]}^{p}

$_{[4×4]}^p$ para 4 alternativas presentadas en la tabla. La relación de preferencia será la matriz

А_{[4 \times 4]}^{p}

$_{[4×4]}^p$ que se ve así:

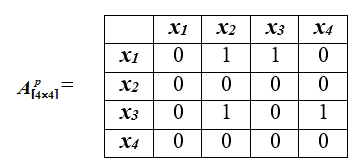
El mapeo del cuadro de mando a la matriz del índice de preferencias es el siguiente:

a_{i, j} = 1

$a_{i,j}=1$ , si:

1) el número de indicadores por los cuales el objeto

x_{i}

$x_i$ preferido sobre el objeto

x_{j}

$x_j$ más que el número de indicadores para los que el objeto

x_{j}

$x_j$ preferido sobre el objeto

x_{i}

$x_i$ ;

2) para el objeto

x_{i}

$x_i$ ninguno de los indicadores toma el valor más pequeño posible.

3) la condición 1 implica que aquellos indicadores para los cuales el objeto

x_{i}

$x_i$ no peor que el objeto

x_{j}

$x_j$ , constituyen la mayoría de todos los indicadores considerados.

Sin embargo, si se cumple esta condición, puede resultar que de acuerdo con aquellos indicadores para los cuales el objeto

x_{i}

$x_i$ peor objeto

x_{j}

$x_j$ , la diferencia es significativa; Para reducir el número de estos casos al dar preferencia ax, se introduce la condición 2.

Métodos para resolver el problema de la toma de decisiones.

Dejemos, después de recibir los datos iniciales, tenemos la relación R sobre el conjunto de alternativas

Ω = (x_{1}, . . ., x_{n})

$Ω= {(x_1, ...,x_n)}$ ... Y la tarea es tomar una decisión. El método principal es el ordenamiento lineal (ranking) de alternativas, es decir, alinear las alternativas en una cadena en orden descendente de su valor, idoneidad, importancia, etc., de la “mejor” a la “peor”.

La relación R puede ser:

actitud no transitiva completa;
una relación de orden parcial;
orden lineal.

Solo en el caso de la linealidad de la relación R, la estructura de preferencias cumple la tarea. En este caso, la clasificación de alternativas del conjunto Ω se obtiene directamente al construir un diagrama de líneas del conjunto ordenado. En el diagrama, la alternativa

x_{i}

$x_i$ , será estrictamente superior a la alternativa

x_{j}

$x_j$ si lo prefiere.

La solución del problema planteado para relaciones completas y transitivas se realiza mediante métodos (algoritmo) de clasificación de alternativas y para órdenes parciales mediante un algoritmo de reordenación lineal. Estos algoritmos se discutirán en los siguientes párrafos a continuación.

Ranking de alternativas . Sea la relación [Ω, R] completa y no transitiva. La propiedad de completitud significa que todas las alternativas

Ω = (x_{1}, . . ., x_{n})

$Ω = {(x_1, ...,x_n)}$ del conjunto son comparables entre sí. La presencia de no transitividad es posible solo si el gráfico de preferencias G [Ω, R] contiene contornos.

Es necesario transformar la estructura del gráfico de relaciones para eliminar las contradicciones lógicas en forma de contornos. Suponiendo que hay un contorno en relación con R

x_{1}, x_{2}, \dots, x_{k}, x_{1},

$x_1, x_2, …,x_k, x_1,$ luego, al clasificar alternativas

x_{1}

$x_1$ debe estar ubicado más alto

x_{2}, x_{3}, \dots, x_{k}, x_{1},

$x_2, x_3, …,x_k, x_1,$ lo que conduce a una contradicción.

Introduzcamos la siguiente afirmación [1,5].

Sean B 'y B "dos contornos arbitrarios de una gráfica de la forma G [Ω, R], entonces si algún elemento

x_{i}

$x_i$ є B 'domina el elemento

x_{j}

$x_j$ є B '', luego cualquier elemento

x_{1}

$x_1$ є B 'cualquier elemento domina

x_{k}

$x_k$ є B ''.

Esta propuesta permite dividir el conjunto R en m subconjuntos

B_{1}, B_{2}, \dots, B_{m}

$B_1, B_2, …,B_m$ tal que

B_{i} \cap B_{j} = \emptyset, \forall i, j є [1, m]; U B_{i} = Ω .

$B_i ∩ B_j=∅, ∀i,j є [1, m]; UB_i =Ω.$

Entonces, el problema de clasificar las alternativas del conjunto se divide en dos etapas:

1) la selección de los contornos del gráfico, es decir, partición del conjunto Ω en subconjuntos

B_{1}, B_{2}, \dots, B_{m}

$B_1, B_2, …,B_m$ y el orden de grupo de estos subconjuntos;

2) clasificación de los elementos de contorno seleccionados en la primera etapa.

Algoritmo para resaltar los contornos de un gráfico

Para encontrar los contornos de un gráfico, existe un algoritmo simple [1]. Permitir

А_{[n \times n]}

$_{[n×n]}$ ¿Es la matriz de adyacencia del gráfico G [Ω, R] y

Е_{[n \times n]}

$_{[n×n]}$ –Matriz unitaria. Formamos

Е_{[n \times n]} + А_{[n \times n]}

$_{[n×n]}+ _{[n×n]}$ ,

(Е_{[n \times n]} + А_{[n \times n]})^{2}

$(_{[n×n]}+ _{[n×n]})^2$ ,

(Е_{[n \times n]} + А_{[n \times n]})^{3}

$(_{[n×n]}+ _{[n×n]})^3$ ,… Una secuencia de grados de matrices, cuyos elementos expresan el número de caminos de longitud como máximo 1, 2, 3… Para algún valor m ≤ n, obtenemos la siguiente igualdad (una matriz estable):

(Е_{[n \times n]} + А_{[n \times n]})^{m} = (Е_{[n \times n]} + А_{[n \times n]})^{m + 1}

$(_{[n×n]}+ _{[n×n]})^m=(_{[n×n]}+_{[n×n]})^{m+1}$ ...

Se sabe por la teoría de grafos [10] que a cada sistema de todas las filas idénticas de una matriz "estable" le corresponde un subconjunto de los vértices del gráfico que se encuentran en un contorno. Agrupando los vértices correspondientes en clases, obtenemos una partición del conjunto original Ω en subconjuntos

B_{1}, B_{2}, \dots, B_{m}

$B_1, B_2, …,B_m$ ...

Es obvio que entre estos subconjuntos uno puede encontrar tal subconjunto

B_{i} m

$B_im$ que los elementos de este subconjunto no estarán dominados por ningún elemento de otros subconjuntos. Este subconjunto será considerado el mejor y ocupará el primer lugar en la clasificación en orden descendente de preferencia.

Luego, encontramos el mejor subconjunto entre los subconjuntos restantes utilizando el mismo principio y lo colocamos en segundo lugar.

Continuaremos con este procedimiento hasta que todos los subconjuntos ocupen sus lugares en el ranking.

Sea la relación de preferencia R dada en el conjunto Ω por la matriz

А_{[6 \times 6]}

$_{[6×6]}$ ...

El gráfico de relación R se muestra en la Fig. GRAMO.

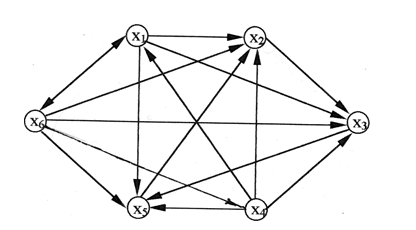
Figura: D. Gráfico de relación no transitiva R

Para implementar la primera etapa de clasificación de los elementos del conjunto, es necesario seleccionar los contornos del gráfico G [Ω, R]. Esto se hace elevando la matriz de adyacencia del gráfico a potencias sucesivas hasta que las matrices coincidan.

Obtenemos

(Е_{[6 \times 6]} + А_{[6 \times 6]})

$(_{[6×6]}+ _{[6×6]})$ ,

(Е_{[6 \times 6]} + А_{[6 \times 6]})^{2}

$(_{[6×6]}+ _{[6×6]})^2$ ,

(Е_{[6 \times 6]} + А_{[6 \times 6]})^{3}

$(_{[6×6]}+ _{[6×6]})^3$ ...

Luego calculamos secuencialmente las potencias crecientes de la matriz, sumándolas con la matriz unitaria de la dimensión correspondiente hasta que la matriz deje de cambiar:

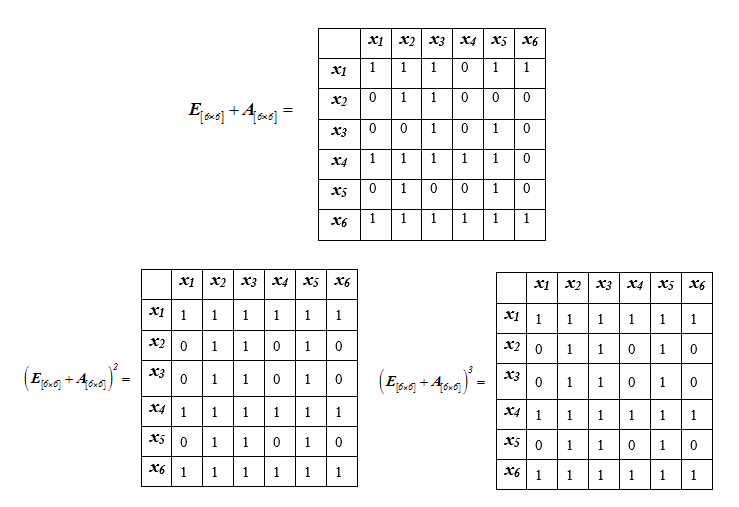
Porque

(Е_{[6 \times 6]} + А_{[6 \times 6]})^{2} = (Е_{[6 \times 6]} + А_{[6 \times 6]})^{3}

$(_{[6×6]}+ _{[6×6]})^2 =(_{[6×6]}+ _{[6×6]})^3$ , podemos concluir que

(Е_{[6 \times 6]} + А_{[6 \times 6]})^{2} = (Е_{[6 \times 6]} + А_{[6 \times 6]})^{k}

$(_{[6×6]}+ _{[6×6]})^2 = (_{[6×6]}+ _{[6×6]})^k$ , para k ≥ 2. Del análisis de la matriz

(Е_{[6 \times 6]} + А_{[6 \times 6]})^{2}

$(_{[6×6]}+ _{[6×6]})^2$ de ello se deduce que las líneas correspondientes a los elementos

x_{1}, x_{4}, x_{6}

$x_1,x_4,x_6$ coinciden, esto indica que estos elementos pertenecen al mismo contorno del gráfico G [Ω, R].

Los elementos

x_{1}, x_{4}, x_{6}

$x_1,x_4,x_6$ formar un conjunto

B_{1} = (x_{1}, x_{4}, x_{6})

$B_1 =(x_1,x_4,x_6)$ ... Otro contorno está formado por elementos

x_{2}, x_{3}, x_{5}

$x_2,x_3,x_5$ que están incluidos en el conjunto

B_{2} = (x_{2}, x_{3}, x_{5})

$B_2 =(x_2,x_3,x_5)$ ...

Por lo tanto, hemos dividido el conjunto en m = 2 clases.

B_{1}, B_{2}

$B_1, B_2$ ... Realicemos un pedido grupal de estos subconjuntos. Para hacer esto, necesitas encontrar algún elemento

x_{i} є B_{1}

$x_i є B_1$ que elemento domina

x_{j} є B_{2}

$x_j є B_2$ ...

Esto significará la superioridad del subconjunto

B_{1}

$B_1$ terminado

B_{2}

$B_2$ ... En nuestro ejemplo

x_{1} є B_{1}

$x_1 є B_1$ domina

x_{2} є B_{2}

$x_2 є B_2$ ... Por lo tanto, el subconjunto

B_{1}

$B_1$ domina

B_{2}

$B_2$ ... Una representación gráfica del dominio en la partición Ω se muestra en la Fig. QC.

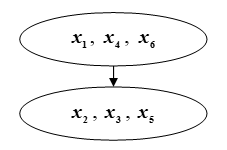
Figura: QC. Ranking de los contornos seleccionados en la primera etapa

Algoritmo para clasificar los elementos de los contornos . ¿Es posible disponer los elementos de una relación que se encuentran en el mismo contorno, son equivalentes entre sí o existen diferencias suficientemente sutiles entre ellos para distinguirlos? Resulta que tal posibilidad, por regla general, existe [1].

Denotemos por

B_{h_{[n \times n]}}

$B_{h_{[n×n]}}$ la matriz de adyacencia del contorno h-ésimo. Introduzcamos el concepto

p^{i} (k)

$p^i(k)$ es la fuerza de orden k del elemento i, cuyo valor se calcula como la suma de los elementos de la i-ésima fila de la matriz

B_{h_{[n \times n]}}^{k}

$B_{h_{[n×n]}}^k$ (1).

Permitir

b_{h_{[i, j]}}^{k}

$b_{h_{[i,j]}}^k$ ¿Es el elemento en la i-ésima fila y j-ésima columna de la matriz, entonces

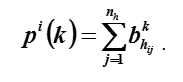
La fuerza relativa del k-ésimo orden del elemento i se entiende como la fracción

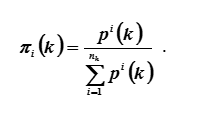
A medida que k aumenta sin acotar (k → ∞), el número

π_{i} (k)

$π_i(k)$ tiende a un cierto límite π, que luego llamaremos la fuerza del elemento i. Vector

П_{[n]} = (π_{1}, . . ., π_{n})

$_{[n]} = (π_1,...,π_n)$ se llama vector límite.

Debido al teorema de Perron-Frobenius [1], el límite siempre existe. El vector propio normalizado de la matriz de adyacencia de contorno coincide con su vector límite. Por tanto, el vector

П_{[n]} = (π_{1}, . . ., π_{n})

$_{[n]} = (π_1,...,π_n)$ (2)

se puede encontrar sin calcular las fuerzas integradas

p^{i} (k)

$p^i(k)$ , resolviendo el sistema de ecuaciones lineales

B_{h_{[n \times n]}} \cdot П_{[n]} = λ П_{[n]}

$B_{h_{[n×n]}} · _{[n]} = λ_{[n]}$ , (3)

donde λ es la raíz real no negativa más grande de la ecuación característica

d e t (λ Е_{[n \times n]} - B_{h_{[n \times n]}}) = 0

$det(λ_{[n×n]}- B_{h_{[n×n]}}) = 0$ (4)

Cabe señalar que el vector propio normalizado de una matriz indecomponible no negativa no cambia cuando la matriz se multiplica por un número s> 0, así como cuando se suma con una matriz de la forma sE.

Luego, los elementos del contorno se ordenan disminuyendo los valores de los componentes vectoriales correspondientes.

П_{[n]}

$_{[n]}$ , es decir el elemento i domina al elemento j cuando

π_{i} > π_{j}

$π_i >π_j$ ...

Clasificaremos los elementos del conjunto

B_{1} = (x_{1}, x_{4}, x_{6})

$B_1 =(x_1,x_4,x_6)$ ... Construyamos una matriz de preferencias para este conjunto

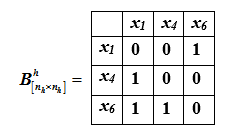
El vector de fuerzas integradas de primer orden para los elementos

(x_{1}, x_{4}, x_{6})

$(x_1, x_4, x_6)$ parece (1,1,2), el vector de fuerzas relativas P (k) = (1 / 4,1 / 4,2 / 4).

Clasificación de artículos

(x_{1}, x_{4}, x_{6})

$(x_1, x_4, x_6)$ la fuerza del primer orden se muestra en la Fig. R.

Figura: R. Clasificación de elementos

Encontremos los vectores que caracterizan las fuerzas de 2º, 3º, 4º y 5º órdenes.

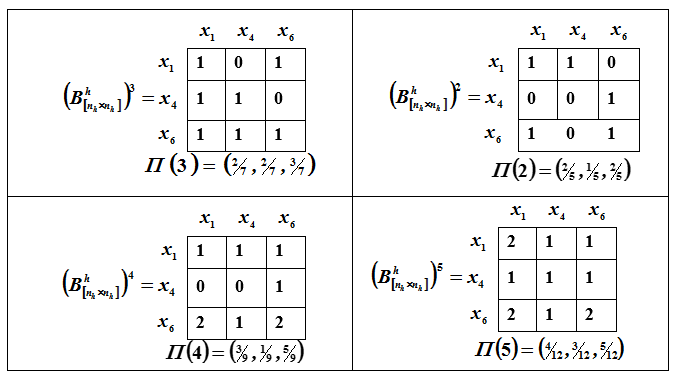
Una representación gráfica de la clasificación se muestra en la Fig. pags.

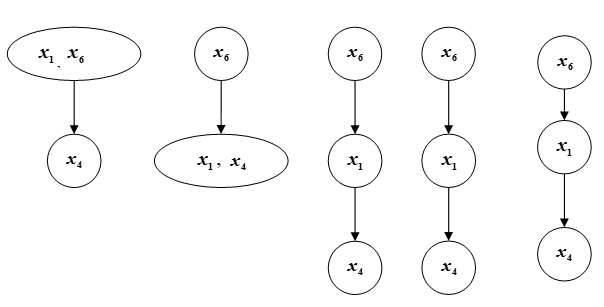
Fig. C - Cadena

Realizando la clasificación de los elementos del conjunto B2 de forma similar, obtenemos los resultados presentados en la Fig. Correcto.

Como resultado de combinar la clasificación de los elementos del conjunto 1 y 2, pasamos al orden final de los elementos del conjunto Ω (Fig. C).

Reordenamiento lineal de órdenes parciales estrictas

Sea la relación R (Fig. A más abajo en el texto), obtenida como resultado de la agregación de juicios individuales de expertos, es una relación de orden parcial en el conjunto Ω. En este caso, Ω es un conjunto ordenado. La construcción de un ordenamiento lineal de alternativas es obtener evaluaciones globales de sus "capacidades" en una escala ordinal.

Por alguna razón, algunos expertos no pueden comparar ciertos pares de alternativas en términos de preferencia. En este caso, la relación agregada R en el conjunto Ω no será un orden lineal. Obviamente, esto conduce al problema del reordenamiento lineal de alternativas a partir de Ω. Este reordenamiento a menudo es posible de muchas formas.

La presencia de múltiples ordenamientos lineales para un ordenamiento parcial indica que el "ordenamiento intrínseco" en la estructura es insuficiente para un solo ordenamiento lineal. Por tanto, se hace necesario resolver el problema del reordenamiento lineal de órdenes parciales. Sea R un orden parcial.

Teorema (Spielrein [5, 10]). Cualquier orden R en un conjunto puede extenderse a un orden lineal en este conjunto.

Un corolario del teorema de Spielrein: cualquier reordenamiento lineal de un subconjunto

Ω_{i} \subseteq Ω

$Ω_i ⊆ Ω$ se puede extender a un reordenamiento lineal de todo el conjunto ordenado Ω.

Si X es un subconjunto en Ω que consta de alternativas incomparables, entonces cualquier ordenamiento lineal de X puede extenderse a un ordenamiento lineal de todo el conjunto Ω. En este caso, el orden de R se expresa en términos de órdenes lineales

R_{i}

$R_i$ ...

En virtud del teorema de Spielrein, en el conjunto Ω existe una numeración

x_{1}, x_{2}, . . ., x_{n}

$x_1, x_2,...,x_n$ elementos de este conjunto. La numeración de un conjunto ordenado de n elementos Ω, con una relación de orden dada R, es un mapeo uno a uno del conjunto Ω en sí mismo, es decir, en {1, 2, ..., n}, en el que el elemento "mayor" con respecto al orden corresponde al número mayor [5]. En lo que sigue, por clasificación de elementos nos referimos a cualquier reordenamiento lineal de este orden. Tenga en cuenta que la numeración de un conjunto ordenado representa su dimensión.

En el caso general, el problema de encontrar ordenamientos lineales adicionales se reduce a encontrar todas las numeraciones admisibles del conjunto ordenado parcial original. Puede escribir todas las permutaciones de elementos de Ω, ¡de las cuales habrá n! y para cada uno verifique la condición de que el elemento “más grande” corresponda al número más grande. Sin embargo, este método de encontrar todos los pedidos adicionales es muy laborioso e ineficaz.

Para un conjunto ordenado Ω con un orden R dado en él, un elemento x 'del conjunto Ω se llama máximo si no hay un elemento x estrictamente mayor, es decir, si x> x 'no se cumple para cualquier x є Ω. Un elemento x '' se llama el elemento más grande del conjunto ordenado [Ω, R] si es más grande que cualquier otro elemento x, es decir, para cualquier x є Ω, x ''> x [5].

Si hay un elemento más grande en un conjunto ordenado, entonces es el elemento máximo. Si un conjunto ordenado tiene un único elemento máximo, entonces será el elemento más grande. En un conjunto parcialmente ordenado, se permiten múltiples elementos máximos.

Para cualquier numeración del conjunto de n elementos Ω, el número N se asigna al elemento máximo. Todas las numeraciones del conjunto Ω se pueden obtener si se conocen todas las numeraciones de todos los subconjuntos obtenidos a partir de Ω eliminando uno de esos elementos máximos. La misma técnica se aplica a cada subconjunto [7]. Considere un algoritmo para construir todas las numeraciones del conjunto ordenado [Ω, R].

1. Se construye un gráfico auxiliar [β, γR] del conjunto ordenado [Ω, R], cuyos vértices satisfacen las condiciones:

a) son subconjuntos de Ω;

b) para dos subconjuntos cualesquiera X, Y є β, es cierto: (X, Y є γR) si el

subconjunto Y se puede obtener del subconjunto X eliminando uno de sus elementos máximos (Fig. A y AA).

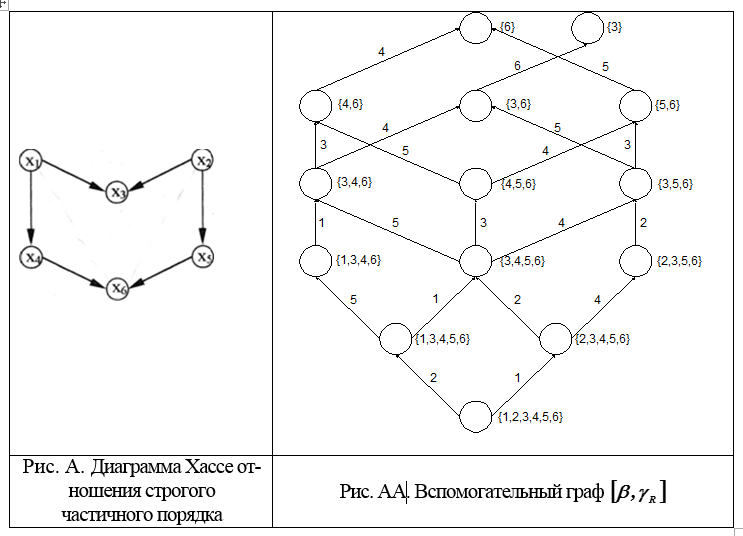
2. Para cada subconjunto de un elemento del conjunto γR, escriba su numeración única. Para obtener todas las numeraciones del subconjunto X, es necesario enumerar todos los subconjuntos adyacentes y que cada subconjunto continúe con todas sus numeraciones. Como resultado, se obtendrán todas las numeraciones del conjunto Ω, es decir, todas las extensiones lineales de orden R.

El problema es encontrar todos los ordenamientos lineales adicionales de un orden parcial, cuyo diagrama se muestra en la Fig. A. No hay información al respecto, por ejemplo, si la alternativa domina

x_{1}

$x_1$ alternativa

х_{2}

$_2$ o viceversa, y también de manera similar para parejas

(х_{3}, х_{6}); (х_{4}, х_{5})

$(_3, _6);(_4, _5)$ ... Esto significa que A es un ordenamiento parcial. Hay muchas (22) opciones para construir un orden lineal, que es deseable llevar a una sola. Esto es posible con la participación de información adicional sobre las alternativas obtenidas de un estudio detallado de la situación.

1. Construimos un gráfico auxiliar [β, γR], comenzando con el conjunto

(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6})

$(x_1, x_2, x_3,x_4, x_5, x_6)$ y por debajo. El número cerca del arco del gráfico indica eliminando qué elemento máximo se obtuvo el subconjunto al que se dirige esta flecha (Fig. AA).

2. Formamos la mesa. AAA para encontrar todas las numeraciones de subconjuntos que son vértices del gráfico [β, γR]. El llenado de la mesa se realiza línea a línea de arriba a abajo. Cada línea es la numeración del subconjunto registrado en la columna izquierda de la tabla (Tabla AAA).

3. Al componer la numeración de un subconjunto X, que consta de k elementos, es necesario reescribir toda la numeración de subconjuntos Y є γR (x) escrita previamente (para el subconjunto anterior) y asignar un número al elemento que complementa Y a X.

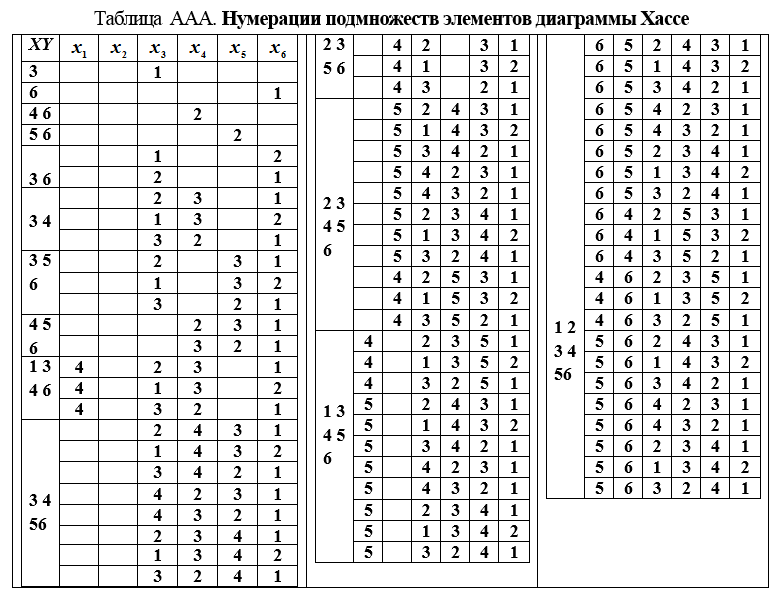
El último bloque (inferior) (Tabla AAA) contiene todas las numeraciones del reordenamiento lineal del conjunto Ω. Una representación gráfica de estos nuevos pedidos se muestra en la Fig. AAA.

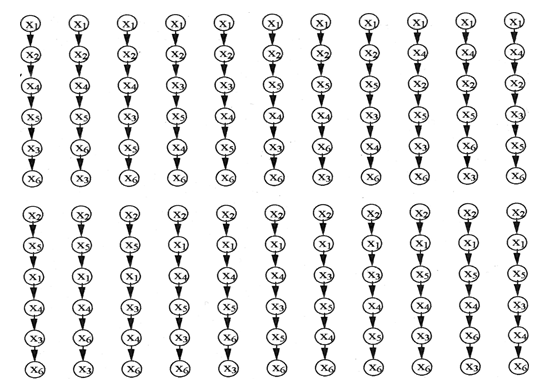
Figura: AAA. Representación gráfica de los pedidos anticipados

Debe tenerse en cuenta que hay 6 pedidos lineales en un conjunto de 6 elementos. o 720, y reordenamiento lineal del conjunto Ω con la relación dada por el gráfico que se muestra en la Fig. AA, 22. Esto también es suficiente para tomar una decisión.

¿Existen oportunidades para reducir el número de tales opciones? Sí hay.

Para reducir el número de pedidos lineales adicionales, debe utilizar información adicional.

Información Adicional

Sea [Ω, R] la relación inicial, entonces la información adicional se puede representar como una razón δ en el conjunto Ω, donde la condición (x, y) є δ, es decir, (x> y) se interpreta como un mensaje de que el objeto x domina al objeto y;

la razón δ puede considerarse entonces como un conjunto de mensajes similares de información sobre dominancia, dado en forma de una razón binaria δ, existen dos casos posibles cuando se usa información adicional:

el gráfico de relación R∪δ contiene contornos;
el gráfico de la relación R∪δ no contiene contornos.

En el primer caso, la ordenación lineal del conjunto Ω con una relación R∪δ determinada se realiza utilizando el algoritmo de clasificación

considerado anteriormente.

En el segundo caso, el ordenamiento lineal del conjunto Ω con la relación R∪δ dada en él se realiza utilizando el algoritmo de reordenamiento lineal

considerado anteriormente. Cabe señalar que la relación R∪δ, que no contiene contornos, puede ser no transitiva y, como resultado, no ser un orden parcial.

Para salir con éxito de esta situación, es necesario que la información adicional δ y la relación inicial R se den en forma de diagramas de Hasse, es decir, sin indicación explícita de enlaces transitivos. El valor de la información adicional vendrá determinado por la cantidad de veces que disminuye el número de pedidos adicionales lineales cuando se utiliza.

Por ejemplo, si se recibe información que

x_{2}

$x_2$ domina

x_{4}

$x_4$ , es decir

x_{2} > x_{4}

$x_2>x_4$ , entonces el número de reordenamientos lineales disminuirá de 22 a 19, y si llega información:

x_{1} > x_{2}

$x_1>x_2$ , entonces el número de pedidos anticipados lineales se reduce a la mitad. Por lo tanto, surge la pregunta: ¿qué información será más valiosa, o si agrega qué razón δ, el número de pedidos adicionales disminuirá más?

Para resolver este problema para todos los pares de elementos

(x_{i}, x_{j})

$(x_i, x_j)$ los conjuntos Ω, que no están incluidos en la relación R, en el bloque inferior de la Tabla. AAA, necesitas calcular

n_{i j}

$n_{ij}$ - cuántas veces el número de artículo

x_{i}

$x_i$ más número de artículo

x_{j}

$x_j$ , es decir elemento

x_{i}

$x_i$ se encuentra por encima del elemento

x_{j}

$x_j$ y

n_{j i}

$n_{ji}$ - cuántas veces un artículo

x_{j}

$x_j$ se encuentra por encima del elemento

x_{i}

$x_i$ ...

El valor de la información adicional sobre la relación en este par será cuanto mayor sea, menor será la diferencia.

| n_{i j} - n_{j i} |

$|n_{ij} - n_{ji}|$ ... Mayor número

n_{i j}, n_{j i}

$n_{ij}, n_{ji}$ será igual al número de reordenamientos del conjunto [Ω, R∩δ]. Para el ejemplo considerado, obtenemos un resumen de las características de la representación gráfica de los reordenamientos

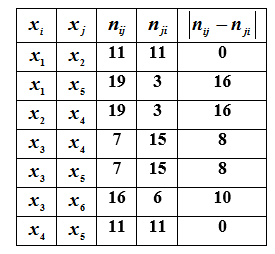
Del análisis de la tabla se desprende que la

información más útil será la información sobre la relación por parejas

(x_{1}, x_{2})

$(x_1, x_2)$ y

(x_{4}, x_{5})

$(x_4, x_5)$ ... La obtención de información adicional sobre la relación en cualquiera de estos pares conduce a reducir a la mitad el número de ordenamientos lineales adicionales.

Conclusión

La formulación y solución del ZPR solo es posible en una situación de muchas alternativas y la elección de la mejor. Si no tiene otra opción, siga el camino en el que se encuentra.

Las decisiones que toma un tomador de decisiones se basan en su preferencia, que se describe mediante una relación de preferencia. La presencia de la relación le permite construir un modelo matemático para la investigación. La incertidumbre en las preferencias se elimina mediante el uso de información adicional que no es experta.

Se presta atención a la consideración de medidas y estimaciones de los valores de los indicadores de propiedades de los objetos. Se dan ejemplos de varias escalas que a menudo se ignoran.

Se enumeran las posibles formulaciones de ZPR y la información necesaria para su solución.

Usando un ejemplo numérico específico, se muestra la aplicación de métodos algebraicos para resolver ZPR, sin el uso de muestras estadísticas y métodos de procesamiento empírico.

El método se basa en el resultado del teorema sobre la posibilidad de extender un orden parcial a uno lineal (perfecto).

Lista de literatura usada

1. Berge K. Teoría de grafos y su aplicación. - M.: IL, 1962 .-- 320 p.

2. Vaulin AE Matemática discreta en problemas de seguridad informática. Part I. SPb.: VKA lleva el nombre de A.F. Mozhaisky, 2015 .-- 219 p.

3. Vaulin AE Matemáticas discretas en problemas de seguridad informática. II. SPb.: VKA lleva el nombre de A.F. Mozhaisky, 2017 .-- 151 p.

4. Vaulin AE Métodos de investigación de complejos informáticos de información. Problema 2. - L .: VIKI ellos. A.F. Mozhaisky, 1984 .-- 129 p.

5. Metodología Vaulin AE y métodos de análisis de sistemas informáticos de información. Edición 1.– L .: VIKI im. A.F. Mozhaisky, 1981 .-- 117 p.

6. Vaulin AE Métodos de procesamiento de datos digitales: transformaciones ortogonales discretas. - SPb.: VIKKI ellos. A.F. Mozhaisky, 1993 .-- 106 p.

7. Kuzmin VB Construcción de soluciones grupales en espacios de relaciones binarias claras y difusas. - M .: Nauka, 1982. - 168 p.

8. Makarov IM et al., La teoría de la elección y la toma de decisiones - Moscú: Fizmatlit, 1982. –328 p. 52.

9. Rosen V.V. Finalidad - optimalidad - solución.- M .: Radio y comunicación, 1982. - 169 p.

10. Szpilraijn E Sur Textension de l'ordre partiel. - Fundam. matemáticas, 1930, vol. 16, págs. 386-389.

Tomando decisiones. Ejemplo