🤯 🍖 ⛹🏼 Opciones: colocación de llamada flotante, movimiento browniano. Programa educativo para geek, parte 7 🛩️ 📉 🔰

Esta es la segunda parte de la historia sobre opciones, en la que nos ocuparemos del aumento de la opción put-call, la condición de no arbitraje de mercado, nos familiarizaremos con las ideas de cobertura y replicación, y hablaremos sobre qué es el movimiento browniano y cómo se relaciona con modelar el comportamiento de la tasa de un activo financiero a lo largo del tiempo.

Habrá un poco de matemáticas para comprender mejor los detalles.

Esta publicación es una transcripción de mis video conferencias " Put-call hover y la condición para la ausencia de arbitraje ", " Movimiento browniano ", creadas como parte del curso Finmath para Fintech.

Poner-llamar flotando. Un ejemplo del uso de la condición de no arbitraje para analizar el precio de una cartera de instrumentos

Entonces, de la parte anterior, sabemos cómo son los pagos de una opción de compra y venta al vencimiento (el momento en el que se puede ejercer el derecho que brinda la opción), pero también nos gustaría saber cómo calcular la opción para otros períodos de tiempo. Para hacer esto, necesitamos construir un modelo matemático utilizando un aparato matemático más complejo. Sin embargo, antes de hacer eso, echemos un vistazo a la relación de paridad put-to-call, que es fácil de calcular y muy útil en la práctica.

Recuerde que una opción europea es un contrato en virtud del cual el comprador del contrato recibe el derecho, pero no la obligación, de comprar o vender algún activo subyacente a un precio predeterminado en un momento específico en el futuro.

El activo subyacente puede ser una acción o un tipo de cambio. La tasa de mercado del activo subyacente se denomina al contado y, en las fórmulas, el valor del contado en ese momento.

t

$t$ denotado como

S_{t}

$S_t$ ...

Una opción que da derecho a comprar el activo subyacente se denomina opción de compra. El derecho a vender es una opción de venta. El precio al que la opción da derecho a concluir un trato en el futuro se llama strike, denotado

K

$K$ ...

La hora acordada previamente en el contrato en la que se puede utilizar la opción es la hora de vencimiento de la opción (vencimiento) -

T

$T$ ... El valor de la tasa del activo subyacente en el momento del vencimiento se indica mediante

S_{T}

$S_T$ ...

Construyamos cronogramas de pago para el vencimiento. Tenemos un determinado activo subyacente, su precio de vencimiento:

S_{T}

$S_T$ así como el pago

P

$P$ Nosotros recibimos. Los horarios de pago estarán en estas coordenadas

S_{T}, P

$S_T, P$ ... Vamos a poner

K

$K$ - nivel de golpe en el eje

S_{T}

$S_T$ ...

La primera opción que sacaremos es una opción de compra. Compramos una opción de compra.

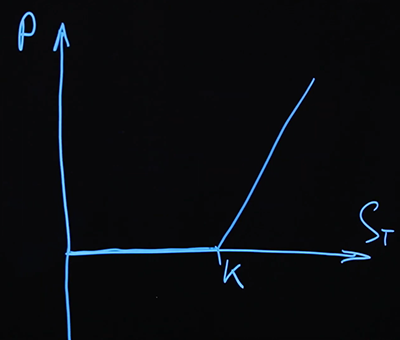
Esto también se llama una opción de compra "larga" , una posición de signo más en esa opción. Pero también podemos vender opciones, esto se llama corto .

La segunda opción que sacaremos será una venta corta .

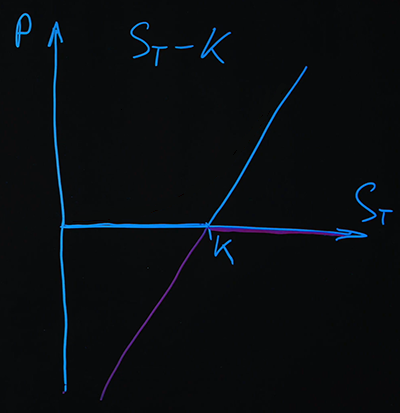
En el gráfico, podemos ver que cuando sumamos los dos pagos, obtenemos una función lineal simple, que se define como (

S_{T} - K

$S_T-K$ ). El mismo resultado se puede obtener analíticamente. Tenemos una posición de opción de compra con un signo más y una opción de venta con un signo menos:

C - P

$C-P$

Usemos las fórmulas analíticas que ya conocemos:

m a x (0, S_{T} - K) - m a x (0, K - S_{T})

$max(0, S_T-K)-max(0, K-S_T)$ ...

Para expandir los corchetes, tenemos que considerar dos casos separados donde

S_{T} > K

$S_T>K$ y

S_{T} < K

$S_T<K$ ...

Contamos con el siguiente sistema:

{\begin{cases} S_{T} - K - 0, S_{T} > K \\ 0 - K + S_{T}, S_{T} \leq K \end{cases}

$\begin{cases} S_T-K-0, S_T>K \\ 0-K+S_T, S_T≤K \end{cases}$

En ambos casos, obtienes la misma fórmula simple:

S_{T} - K

$S_T-K$ ...

Por lo tanto, los pagos se describen en cualquier caso mediante la misma fórmula, independientemente del precio del activo subyacente que se haya realizado en el momento del vencimiento. Nuevamente, les recuerdo que los pagos que hemos retirado son pagos (y por lo tanto el costo) de las opciones en el momento del vencimiento. En el caso de los precios de las opciones en algún otro momento, se describen mediante otras funciones más complejas. Los dibujaré condicionalmente por ahora.

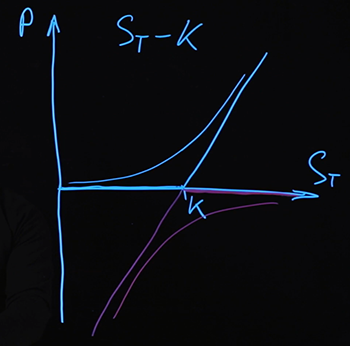
Sabemos que para esta combinación en el momento del vencimiento, el pago está determinado por la fórmula

S_{T} - K

$S_T-K$ , por cualquier valor

S_{T}

$S_T$ ... Si encontramos alguna otra combinación de instrumentos que dará el mismo pago en el momento del vencimiento, entonces podemos decir que el costo de tal combinación de instrumentos y combinación

C - P

$C-P$ debería ser el mismo.

Si este no fuera el caso, hoy puede comprar el más barato de estas combinaciones de instrumentos y vender el más caro, obteniendo así una ganancia. Y dado que estas dos combinaciones dan el mismo pago al vencimiento, y las tomamos con signos opuestos, se garantiza que el pago total será cero. Tal transacción, que da un ingreso garantizado sin riesgo, simplemente por el desequilibrio en los precios de los instrumentos en el mercado, se llama arbitraje.... Las teorías matemáticas para calcular los precios de los instrumentos generalmente incluyen el supuesto de que el mercado está libre de arbitraje. Esta suposición coincide bastante bien con la realidad. Las oportunidades de arbitraje en el mercado, si surgen, no duran mucho. Encontrarlos y usarlos no es fácil. Entonces, normalmente, esta suposición funciona bien.

De la condición de que el mercado esté libre de arbitraje, se sigue que la combinación

C - P

$C-P$ será en cualquier momento

t \leq T

$t≤T$ (no solo

T

$T$ ) cuestan lo mismo que cualquier combinación de instrumentos, cuyo pago en el momento

T

$T$ será igual

S_{T} - K

$S_T-K$ ... Esta combinación es fácil de hacer comprando el activo subyacente.

S

$S$ y pedir prestado dinero en tal cantidad que al momento del vencimiento será necesario devolver una cantidad igual a

K

$K$ ... Cuando se trata de instrumentos financieros, dicha deuda equivale a vender un bono cupón cero (bono), lo que da un pago

K

$K$ En el momento

T

$T$ ... Puede leer más sobre bonos e intereses en publicaciones anteriores de esta serie ( Valor del dinero, tipos de interés, tipos de descuento y futuros. Programa educativo para un geek, parte 1 y Bonos: cupón y cupón cero, cálculo de rendimiento. Programa educativo para un geek, parte 2 ) ...

Entonces, una cartera de una opción de compra y una cartera de una opción de venta es igual a la combinación de un largo para el activo subyacente y un bono corto, lo que daría un pago por vencimiento con un par

K

$K$ ...

C_{t} - P_{t} = S_{t} - B_{T} K

$C_t-P_t=S_t-B_TK$

Esta relación es independiente del modelo que podríamos construir para la tasa de activo subyacente. Ni siquiera depende de cómo consideremos el descuento, y esto se deriva de la ausencia de arbitraje en el mercado. Hemos compilado una cartera, hemos considerado todas las opciones posibles, cuánto puede costar al vencimiento, y descubrimos que en todas las opciones para el futuro cuesta exactamente lo mismo. Por lo tanto, si otra cartera tiene exactamente el mismo pago por vencimiento, su precio debería ser el mismo.

Entonces, obtuvimos la proporción para una cartera de opciones de compra y venta. Hemos compilado una cartera, examinado qué tipo de pago tendrá en el momento del vencimiento y descubrimos que el pago se describe mediante una ecuación lineal. A diferencia de la función de pago para las opciones de compra y venta, cada una de las cuales tiene dos secciones, más y menos

S_{T}

$S_T$ ... Esto le permite crear una cartera de instrumentos más simples que le darán el mismo pago al vencimiento en cualquier situación. El precio de estas dos carteras será igual en cualquier momento, no solo en el momento de su vencimiento. Esto está garantizado por la condición de que no haya arbitraje en el mercado. Si hay arbitraje en el mercado y esta igualdad no se satisface, entonces, en consecuencia, podemos comprar una de estas carteras, vender otra y obtener una ganancia garantizada. Esta relación no depende de ningún modelo matemático que podamos construir, por ejemplo, para el precio del activo subyacente. Esta relación debe cumplirse en cualquier modelo.

También puede ver esta relación de esta manera. Hemos compilado una cartera de varios activos con el mismo riesgo. La fórmula se puede reescribir para recopilar activos que conllevan el riesgo asociado con el activo subyacente, por un lado. Es decir, podemos eliminar todo el riesgo inherente a estos instrumentos, es decir, incertidumbre asociada con el precio futuro del activo subyacente, sabiendo exactamente cuánto vale dicho paquete.

C_{t} - P_{t} - S_{t} = - B_{t} K

$C_t-P_t-S_t=-B_tK$

Esta forma de deshacerse del riesgo se llama cobertura . Compusimos una cartera de varios instrumentos en los que está incrustado parte del mismo riesgo, pero los seleccionamos en tales proporciones que estos riesgos se equilibran mutuamente y nos deshacemos de ellos. Esta idea se utiliza en otras estrategias de cobertura más complejas. El caso en consideración es muy simple, le permite trabajar solo con una cierta combinación de opciones.

Si miramos esta idea desde el otro lado, entonces podríamos expresar una de estas herramientas a través de otras. Por ejemplo, si tenemos una cosa en el mercado, una opción de venta, automáticamente recibiremos una opción de compra. En este caso, será replicación- replicamos el pago de un producto a través de otros. La cobertura y la replicación están íntimamente relacionadas entre sí, matemáticamente, son cálculos muy similares.

En este caso, tenemos una situación muy simple, y para cubrir completamente el riesgo o replicar el pago, solo necesitamos crear una cartera una vez, y luego esperamos hasta el momento de vencimiento, el pago ya está garantizado. Esto se denomina replicación estática ( cobertura estática). Este es un caso raro y generalmente no funciona. Para lograr este efecto de manera más general, será necesario recurrir a estrategias de cobertura dinámica. Es decir, haremos una cartera una vez, pero luego constantemente necesitaremos agregar algo o cambiar algo allí, para que el pago en el momento de la expiración resulte exactamente como queremos.

Aquí hay una relación interesante de aumento vertiginoso de la opción put-call. A pesar de que las matemáticas son muy simples, en su ejemplo se pueden ver varias ideas muy importantes que se aplican en un caso más complejo: la aplicación de la condición de no arbitraje, la replicación de pagos y la cobertura de riesgos. Aquí es donde terminamos con esta relación simple y podemos pasar a construir un modelo más complejo.

Nos gustaría construir un modelo que diera no solo la relación entre las opciones de compra y venta, sino también el precio de la opción en función de los valores observados en el mercado. Esto requerirá una teoría matemática más compleja.

Qué es el movimiento browniano y quién es Robert Brown. Cómo simular el movimiento browniano en una computadora. ¿Qué es el movimiento browniano geométrico?

Lo que hemos considerado hasta ahora nos permitió arreglárnoslas con un aparato matemático muy simple, de hecho, las matemáticas escolares. Para avanzar y construir un modelo matemático más complejo, esto no será suficiente para nosotros, y se requieren elementos de matemáticas "adultas". Por lo tanto, el enfoque general para la presentación posterior se verá así: daré ejemplos ilustrativos a partir de los cuales quedará claro cómo funciona el aparato matemático en un caso simple, y también daré formulaciones y teoremas que usaremos. No probaré estos teoremas. Aquellos que estén interesados en la parte de matemáticas pueden consultar los libros de texto y cursos de video correspondientes.

El primer concepto que necesitamos es el movimiento browniano.... Recordemos lo que significa este término en física. Este será una especie de ejemplo claro de cómo se organizará este proceso en nuestro modelo matemático formal.

Creo que mucha gente usa el término " movimiento browniano"asociado con el plan de estudios de física escolar. Muchos creen que la persona que introdujo este concepto en la circulación científica fue un físico de nombre Brown y, a juzgar por el nombre, era un inglés. Curiosamente, todas estas suposiciones son incorrectas. Primero, el nombre de este científico era Robert Brown, que en ruso debería leerse como “Robert Brown”. Aunque esto podría no ser obvio para una persona educada de los siglos XVIII y XIX, cuyo primer idioma extranjero fue el francés y el segundo alemán. En segundo lugar, no era inglés, era escocés, lo que, según entendemos, no es en absoluto lo mismo. Pero lo más interesante es que no era físico, era botánico. Cuando realizó y describió su famoso experimento, estaba estudiando partículas de polen bajo un microscopio. La muestra del portaobjetos se preparó en forma de gota de líquido, en la que se colocaron partículas de polen parapara que el polen no salga volando de cada corriente y se pueda ver con calma.

Se llamó la atención de Brown sobre el hecho de que lo que ve en el ocular del microscopio no es una imagen estática. Observó, relativamente hablando, una partícula redonda que hacía un movimiento caótico. Hoy sabemos que este fenómeno tiene una explicación sencilla. Hay muchas moléculas en la solución alrededor de esta partícula, que muy a menudo interactúan con ella en una dirección aleatoria, como resultado de lo cual la partícula realiza algún tipo de movimiento complejo.

Si representamos su movimiento, será una trayectoria aleatoria.

¿Qué tiene esto que ver con nuestra área temática? De hecho, la analogía es sencilla. Consideramos la tasa de un activo financiero a lo largo del tiempo. Muchos factores aleatorios actúan sobre él, así como sobre esa partícula, en todo momento. No los vemos, al igual que Robert Brown no vio moléculas individuales a través de un microscopio.

El efecto acumulativo de estos factores aleatorios conduce a un cambio en el curso del activo, al igual que el efecto acumulativo de las moléculas conduce al desplazamiento de una partícula de polen. Estos procesos ocurren continuamente en el tiempo. Y así se realiza la tasa del activo financiero. La dependencia del curso en el tiempo se obtiene al azar y, por lo tanto, dicha trayectoria se llama movimiento browniano. En nuestro caso, este es un movimiento browniano unidimensional, ya que las desviaciones aleatorias ocurren solo alrededor de un eje.

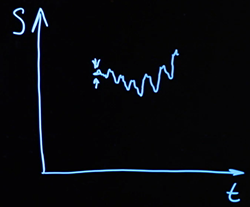
El modelo matemático formal del proceso que usaremos está asociado con el nombre de otro científico, el matemático estadounidense Norbert Wiener. Se parece a esto. Estamos considerando una función de tiempo continuo. Porque el

t

$t$ es continua, entonces la función

W (t)

$W(t)$ continuo.

Contiene un componente aleatorio, que se determina matemáticamente de la siguiente manera:

△ W_{△ t}

$\triangle W_{\triangle t}$ - independiente siempre que los incrementos de tiempo no se crucen.

Incremento de función desde el punto de tiempo

t

$t$ hasta el momento

t + s

$t+s$ distribuido normalmente con parámetros 0 y

s

$s$ (la duración del intervalo de tiempo).

W_{t + s} - W_{t} \sim N (0, s)

$W_{t+s}-W_t∼N(0,s)$

En lo que sigue, veremos que es muy importante poder generar tales rutas en una computadora, esto es necesario para muchos métodos computacionales. ¿Cómo podemos hacer esto? El tiempo, que es continuo en un modelo matemático teórico, lo dividimos en una computadora en algunos incrementos, generalmente con un paso fijo. Creamos un determinado punto de partida desde el que comienza nuestro proceso, con coordenadas

W_{0}; t_{0}

$W_0;t_0$ ... Además, para cada paso de tiempo subsiguiente, generamos una variable aleatoria con tal distribución, avanzamos un paso. Hacemos esto en cada punto. El resultado es una línea discontinua.

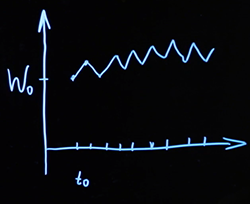
En algún lugar, el incremento resultó con un signo más, en algún lugar con un signo menos. Como resultado, en cada punto específico, el valor de todo el proceso está determinado por la suma acumulada de todas estas variables aleatorias. Para poder escalar el desplazamiento promedio por unidad de tiempo, también podemos introducir un parámetro adicional, generalmente denotado por la letra

σ

$\sigma$ (como para la distribución normal). Podemos considerar la función

σ W_{t}

$\sigma W_t$ dónde

W_{t}

$W_t$ Es el movimiento browniano estándar, y

W_{t}

$W_t$ tiene una varianza más amplia o más estrecha, según lo que necesitemos.

Con tal proceso implementado, nos gustaría construir un modelo matemático que nos ayude a calcular el precio de las opciones. Construyamos ecuaciones de acuerdo con el mismo principio que hicimos con interés para el descuento en tiempo continuo. Esta será una especie de ecuación diferencial.

Si resolviéramos el problema de calcular el interés en una determinada cantidad

P

$P$ en tiempo continuo, entonces por un pequeño paso de tiempo tendríamos la relación correcta

△ P = r P △ t

$\triangle P=rP\triangle t$ o

\frac{△ P}{P} = r △ t

$\frac{\triangle P}{P}=r\triangle t$ ,

donde

r

$r$ Es una tasa de interés neutral al riesgo. Y yendo al limite

Δ t \to d_{t}

$Δt →d_t$ , obtenemos la ecuación diferencial

\frac{d P}{P} = r d t

$\frac{dP}{P}=rdt$ ...

De él obtenemos la fórmula ya familiar para el descuento en tiempo continuo.

P = P_{0} e^{r t}

$P=P_0e^{rt}$ dónde

P_{0}

$P_0$ Es el valor inicial.

Me gustaría adaptar esta lógica de razonamiento a un modelo matemático de un activo, cuyo precio en el futuro depende de factores aleatorios. El cambio relativo en el precio de nuestro activo se caracteriza por un cierto parámetro, un análogo de la tasa neutral al riesgo (en este caso, el parámetro caracteriza nuestro activo subyacente, no es una tasa neutral al riesgo). Agreguemos a esta expresión un componente probabilístico que sería descrito por el movimiento browniano.

\frac{Δ S}{S} = μ Δ t + σ Δ W

$\frac{ΔS}{S}=μΔt+σΔW$

Prácticamente tenemos un resultado. Vayamos al límite y obtengamos una ecuación muy similar a la que resolvimos fácilmente para el descuento de tiempo continuo.

\frac{d S}{S} = μ d t + σ d W

$\frac{dS}{S}=μdt+σdW$

Pero hay un problema técnico. El punto es que el movimiento browniano (proceso de Wiener), como lo definimos, es una función continua del tiempo, pero no es diferenciable en el sentido del análisis matemático clásico. Esto se puede probar formalmente (omitimos la prueba).

Para construir tal modelo matemáticamente rigurosamente, es necesario determinar qué significado le damos a la expresión

d W

$dW$ ... Para esto, es necesario usar un diferencial estocástico, cuyo nombre está asociado con el nombre de otro matemático: el diferencial Ito . Obedece reglas diferentes a las que estamos acostumbrados en el cálculo convencional.

Como referencia, escribiré los resultados que necesitamos con respecto a este aparato matemático. El diferencial Ito obedece a tales reglas.

Si

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ ,

Entonces

f (x, t)

$f(x,t)$ :

d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial x} d x + \frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}} d x^{2}

$df=\frac{∂f}{∂t}dt+\frac{∂f}{∂x}dx+\frac{1}{2}\frac{∂^2f}{∂x^2}dx^2$ ...

Esta regla difiere de la forma en que diferenciamos una función de dos variables en el cálculo convencional. Si tenemos dos variables independientes, en cálculo ordinario tomamos derivadas parciales y nos detenemos en los dos primeros términos de la expansión. El tercer componente de la expansión del diferencial de una función en la fórmula Ito aparece precisamente porque no estamos trabajando con funciones ordinarias, sino con un proceso estocástico aleatorio. Tomamos este resultado listo para usar, sin probarlo.

Hay más que decir sobre

d x^{2}

$dx^2$ en la última ecuación. Por condición

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ , si lo cuadramos, habrá términos con factores

d t d W_{t}

$dt dW_t$ ,

d t^{2}

$dt^2$ ,

d W_{t}^{2}

$dW^2_t$ ... Para aplicar la fórmula de Ito, debe tomar:

d t d W_{t} = 0

$dt dW_t=0$ ;

d t^{2} = 0

$dt^2=0$ ;

d W_{t}^{2} = d t

$dW^2_t=dt$ ...

Todas estas reglas se vuelven naturales si comprendes qué es la integral de Ito, pero para nuestros propósitos ahora es suficiente saber cómo aplicar correctamente la fórmula de Ito.

Y ahora podemos superar nuestra complejidad técnica, ya que sabemos operar con un objeto

σ d W

$σdW$ ...

Como variable

x

$x$ tenemos la tasa de activos subyacente

S

$S$ , podemos expresarlo:

d S = S μ d t + σ S d W_{t}

$dS=Sμdt+σSdW_t$ ...

A continuación, sabemos cómo escribir el diferencial de la función, donde hay

S

$S$ y

t

$t$ ... Veamos cuál es el diferencial de la función

f (S, t) = l n (S)

$f(S, t)=ln⁡(S)$ ...

d l n S = d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial S} d S + \frac{1}{2} \frac{d^{2} f}{d S^{2}} d S^{2} =

$dln S = df = \frac{∂f}{∂t}dt+\frac{∂f}{∂S}dS+\frac{1}{2}\frac{d^2f}{dS^2}dS^2=$

= 0 d t + \frac{1}{S} (S μ d t + σ S d W_{t}) - \frac{1}{2} \frac{1}{S^{2}} σ^{2} S^{2} d t

$=0 dt+\frac{1}{S}(Sμdt+σSdW_t)-\frac{1}{2}\frac{1}{S^2}\sigma^2 S^2 dt$

Ahora, al recopilar los términos, obtenemos una expresión para el logaritmo

S

$S$ ...

d ㏑ S = (μ - \frac{σ^{2}}{2}) d t + σ d W

$d㏑S=(μ-\frac{\sigma^2}{2})dt+σdW$

Ahora sabemos lo que es igual a

㏑ S

$㏑S$ (tenga en cuenta que tiene una distribución normal). Estamos interesados directamente en la expresión para

S

$S$ ...

S = S_{0} e^{μ t} e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$S=S_0 e^{μt}exp(σW_t-\frac{\sigma^2}{2}t)$

La expresión anterior describe el movimiento browniano geométrico . Representa un crecimiento exponencial con el parámetro

μ

$\mu$ que inicialmente comienza en el punto

S_{0}

$S_0$ , y el ruido se superpone alrededor de este exponente según la expresión

e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$exp(\sigma W_t-\frac{\sigma^2}{2}t)$ ... Esto ya se puede leer en una computadora, podemos generar caminos de movimiento browniano. Obtendremos algunas posibles realizaciones de nuestro camino para la tasa de activo subyacente. Hay dos parámetros en esta ecuación:

σ

$\sigma$ - varianza y

μ

$\mu$ - deriva. Corresponden a la varianza de la distribución normal y al sesgo de la distribución normal para

㏑ S

$㏑S$ ... Como dije, ahora es posible simular en una computadora, pero hay un componente teórico más que debemos introducir para que podamos calcular el precio de las opciones usando este proceso. A continuación, hablaremos de medidas neutrales al riesgo.

Todos los artículos de esta serie

Opciones: colocación de llamada flotante, movimiento browniano. Programa educativo para geek, parte 7

Poner-llamar flotando. Un ejemplo del uso de la condición de no arbitraje para analizar el precio de una cartera de instrumentos

Qué es el movimiento browniano y quién es Robert Brown. Cómo simular el movimiento browniano en una computadora. ¿Qué es el movimiento browniano geométrico?

More articles: