Código Reed-Solomon

Una tarea importante de la codología en el procesamiento de flujos de información de mensajes codificados en los canales de los sistemas de comunicación y la computadora es la separación de los flujos y su selección de acuerdo con las características dadas. El flujo dedicado se divide en mensajes separados y para cada uno de ellos se realiza un análisis en profundidad para establecer el código y sus características, seguido de la decodificación y el acceso a la semántica del mensaje.



Entonces, por ejemplo, para un cierto código Reed-Solomon (código de PC), debe configurar:

• la longitud n de la palabra de código (bloque);
• el número de k información y Nk símbolos de verificación;
• un polinomio irreducible p (x) que define un campo finito GF (2 ^r );
• elemento primitivo α de un campo finito;
• generar polinomio g (x);
• parámetro j del código;
• entrelazado usado;
• secuencia de transmisión de palabras de código o símbolos al canal y algunos otros.

Aquí, se considera un problema particular ligeramente diferente en el trabajo: el modelado del código de la PC, que es la parte central principal del problema de análisis de código anterior.

Descripción del código de PC y sus características

Para mayor comodidad y una mejor comprensión de la esencia del dispositivo de código de PC y el proceso de codificación, primero presentamos los conceptos y términos (elementos) básicos del código.



Los códigos Reed - Solomon (código RS) se pueden interpretar como códigos BCH no binarios (Bose - Chowdhury - Hawkingham), cuyos valores de los símbolos de código se toman del campo GF (2 ^r ), es decir, r símbolos de información se muestran como un elemento separado del campo. Los códigos Reed-Solomon son códigos cíclicos sistemáticos lineales no binarios cuyos símbolos son secuencias de r bits, donde r es un número entero positivo mayor que 1.



Los códigos Reed-Solomon (n, k) se definen en símbolos de r-bit para todos n y k, para el cual:

0 <k <n <2 ^r + 2, donde

k es el número de símbolos de información a codificar,

n es el número de símbolos de código en el bloque codificado.



Para la mayoría de los códigos Reed-Solomon (n, k); (n, k) = (2 ^r –1, 2 ^r –1–2 ∙ t), donde

t es el número de símbolos erróneos que el código puede corregir y

n - k = 2t es el número de símbolos de verificación.



El código Reed-Solomon tiene la mayor distancia mínima (el número de caracteres que distinguen las secuencias) posible para un código lineal. Para los códigos Reed - Solomon, la distancia mínima se define de la siguiente manera: dmin = n - k +1.



Definición . Código de PC sobre el campo GF (q = ^m ), con longitud de bloque n = q ^m-1, corrigiendo t errores, es el conjunto de todas las palabras de código u _(n) sobre GF (q) para las cuales 2t componentes de espectro consecutivos con números$$$m_0,m_0 +1,...,m_0+2t-1$igual a 0.



El hecho de que 2t potencias consecutivas de α sean raíces del polinomio generador g (x) o que el espectro contenga 2t componentes cero consecutivos es una propiedad importante del código que permite corregir t errores.



Polinomio de información Q. Especifica el texto del mensaje, que se divide en bloques (palabras) de longitud constante y se digitaliza. Esto es lo que se va a transmitir en el sistema de comunicación.

La generación del polinomio g (x) de un código de PC es un polinomio que transforma los polinomios de información (mensajes) en palabras de código al multiplicar Q · g (x) = = u _(n) sobre GF (q).



El polinomio de verificación h (x) le permite establecer la presencia de caracteres distorsionados en una palabra.

Polinomio del síndromeS (z). Un polinomio que contiene componentes correspondientes a posiciones erróneas. Calculado para cada palabra recibida por el decodificador.

Polinomio de error E. Un polinomio con una longitud igual a la palabra de código, con valores cero en todas las posiciones, excepto aquellas que contienen distorsiones de los símbolos de la palabra de código.



El polinomio localizador de errores Λ (z) proporciona raíces que indican las posiciones de los errores en las palabras recibidas por el lado receptor del canal de comunicación (decodificador). Sus raíces se pueden encontrar por ensayo y error, es decir sustituyendo a su vez todos los elementos del campo hasta que Λ (z) sea igual a cero.

El polinomio de valores de error Ω (z) ≡Λ (z) S (z) (modz ^2t ) es comparable módulo z ^2tcon el producto del polinomio localizador de errores por el polinomio sindrómico.



Polinomio irreducible del campo p (x). Los campos finitos no existen para ningún número de elementos, pero solo si el número de elementos es un número primo p o una potencia q = p ^{m de un} número primo. En el primer caso, el campo se denomina simple (sus elementos son el residuo de números módulo a primo p), en el segundo, es una extensión del campo primo correspondiente (sus q elementos de polinomios de grado m-1 o menos son los residuos de polinomios módulo el polinomio p (x) de grado m)



Polinomio primitivo . Si la raíz de un polinomio irreducible del campo es un elemento primitivo α, entonces p (x) se llama polinomio primitivo irreducible .



En el transcurso de describir acciones con el código de PC, necesitaremos referirnos repetidamente al campo de Galois, por lo tanto, inmediatamente aquí colocaremos una hoja de trabajo con los elementos de este campo con diferentes representaciones de los elementos (número decimal, vector binario, polinomio, grado de un elemento primitivo ).



Tabla II - Características de los elementos del campo finito de la extensión GF (2 ⁴ ), polinomio irreducible p (x) = x ⁴ + x + 1, elemento primitivo α = 0010 = 2 ₁₀





Ejemplo 1 . Sobre un campo finito GF (2 ⁴ ), se da un polinomio de campo irreducible p (x) = x ⁴ + x + 1, se da un elemento primitivo α = 2, y se da un (n, k) - código Reed-Solomon (código PC). La distancia de código de este código es d = n - k + 1 = 7. Este código puede corregir hasta tres errores en el bloque (palabra de código) del mensaje.



El polinomio generador g (z) del código tiene grado m = nk = 15-9 = 6 (sus raíces son 6 elementos del campo GF (2 ⁴ ) en notación decimal, es decir, elementos 2, 3, 4, 5, 6, 7) y está determinada por la relación, es decir polinomio en z con coeficientes (elementos) de GF (2 ⁴ ) en representación decimal para i = 1 (1) 6. En el código PC considerado 2 ⁹ = 512 palabras de código.

Codificación de mensajes de PC

En la tabla II, estas raíces también tienen una representación de poder $$$α^1=2, α^2=3,...,α^6=7$...





Aquí z es una variable abstracta y α es un elemento primitivo del campo, a través de sus poderes se expresan todos los (16) elementos del campo. La representación polinomial de elementos de campo utiliza la variable x.

El cálculo del polinomio generador g (x) = A B del código de PC se realiza en partes (tres corchetes cada una):





La representación vectorial (en términos de los coeficientes g (z) por los elementos del campo en representación decimal) del polinomio generador es



g (z) = G _<7> = (1, 11, 15, 5, 7, 10, 7).



Después de la generación del polinomio generador del código PC orientado a la detección y corrección de errores, se establece un mensaje. El mensaje se presenta en forma digital (por ejemplo, código ASCII), a partir del cual se pasa a la representación polinomial o vectorial.



Un vector de información (palabra de mensaje) tiene k - componentes de (n, k). En el ejemplo k = 9, el vector es de 9 componentes, todos los componentes son elementos del campo GF (2 ⁴ ) en representación decimal Q _<9> = (11, 13, 9, 6, 7, 15, 14, 12, 10) ...



La palabra de código u se forma a partir de este vector_<15> es un vector con 15 componentes. Las palabras de código, como los propios códigos, son sistemáticas y no sistemáticas. Una palabra de código no sistemática se obtiene multiplicando el vector de información Q por el vector correspondiente al polinomio generador



Después de las transformaciones, obtenemos una palabra de código (vector) no sistemática en la forma

Q · g = <11, 15, 3, 9, 6, 14, 7, 5, 12, 15, 14, 3, 3, 7, 1>.



En la codificación sistemática, un mensaje (vector de información) está representado por un polinomio Q (z) en la forma Q (z) = q (z) g (z) + R (z), donde el grado degR (z) <m = 6. Después de eso, para al vector Q de la derecha se le asigna el resto R (todo en forma decimal). Esto se hace así.



El polinomio Q se desplaza hacia los dígitos superiores por el valor m = n - k, que se logra multiplicando Q (z) por Z ^{n - k} (en el ejemplo Z ^{n - k} = Z ⁶ ) y después del desplazamiento, la división Q (z) Z ^{n - k} por g (z). Como resultado, encuentre el resto de la división R (z). Todas las operaciones se realizan en el campo GF (2 ⁴ )



(11, 13, 9, 6, 7, 15, 14, 12, 10, 0, 0, 0, 0, 0, 0) =

= (1, 11, 15, 5, 7, 10, 7) ( 11, 15, 9, 10,12,10,10,10,10,3) + (1, 2, 3, 7, 13, 9) = G · S + R.



El resto de la división de polinomios se calcula de la forma habitual ( ver esquina aquí Ejemplo 6 ). La división se realiza de acuerdo con el patrón: Sea Q = 26, g (z) = 7 luego 26 = 7 3 + R (z), R (z) = 26 -7 3 = 26-21 = 5. Cálculo del resto R (z ) sobre la división de polinomios. Asignamos el resto R al vector Q de la derecha.



Obtenemos u _<15> , una palabra de código en forma sistemática. Esta vista contiene claramente un mensaje de información en los k bits de orden superior de la palabra de código



u _<15> = (11,13,9,6,7,15,14,12,10; 1, 2, 3, 7, 13, 9)



Los dígitos del vector se numeran de derecha a izquierda desde 0 (1) 14. Los seis bits menos significativos de la derecha son los de verificación.

Decodificación de códigos Reed-Solomon

Después de recibir un bloque, el decodificador procesa cada bloque (palabra de código) y corrige los errores que ocurrieron durante la transmisión o el almacenamiento. El decodificador divide el polinomio resultante por el polinomio generador del código RS. Si el resto es cero, entonces no se encontraron errores; de lo contrario, se producirán errores.



Un decodificador de PC típico realiza cinco pasos en un bucle de decodificación, a saber:

1. Cálculo del polinomio sindrómico (sus coeficientes), se encuentran errores.
2. Se resuelve la ecuación clave de Pade, calculando los valores de error y sus posiciones de las ubicaciones correspondientes.
3. Se implementa el procedimiento de Chen: encontrar las raíces del polinomio del localizador de errores.
4. El algoritmo de Forney se utiliza para calcular el valor de error.
5. Se hacen correcciones a las palabras de código distorsionadas;

El ciclo finaliza extrayendo el mensaje de las palabras de código (eliminando el código).



Cálculo del síndrome.



La generación del síndrome a partir de la palabra de código recibida es el primer paso en el proceso de

decodificación. Aquí se calculan los síndromes y se determina si hay errores en la palabra de código recibida o no La



decodificación de las palabras de código de PC se puede organizar de diferentes formas. Los métodos clásicos incluyen la decodificación utilizando algoritmos que operan en el dominio del tiempo o de la frecuencia, que utilizan el cálculo del síndrome o no. Sin profundizar en la teoría de esta cuestión, optaremos por la decodificación con el cálculo de síndromes de palabras en clave en el dominio del tiempo.

Detección de distorsión

Sindrómico $$$S = (S_v,S_{v+1},...,S_{m+v-1})$dónde $$$v∊{0, 1}$el vector se determina secuencialmente para cada una de las palabras de código recibidas por el decodificador en su entrada. Con valores cero de los componentes del vector síndrome$$$Sj = 0, j=v,v+1,...,m + v - 1$, el decodificador considera que no hay error en la palabra recibida. Si por al menos uno$$$j≥1,Sj≠0$, entonces el decodificador concluye que hay errores en el vector de código y procede a identificarlos, que es el primer paso en la operación del decodificador.



El cálculo de la

multiplicación del polinomio sindrómico en el lado receptor de la palabra de código C por la matriz de verificación de paridad H puede dar como resultado dos resultados:

• vector síndrome S = 0, que corresponde a la ausencia de errores en el vector C;
• vector síndrome S ≠ 0, que significa la presencia de errores (uno o más) en los componentes del vector C.

El segundo caso es de interés.



El vector de código con errores se representa como C (E) = C + E, E es el vector de error. Luego$$$(C +E)H^t = CH^t + EH^t = 0 + EH^t = S$



Los componentes Sj del síndrome están determinados por la relación de suma

para n = q-1 yj = 1 (1) m = nk, o por el esquema de Horner:



$$$S_j = C_0 +α^j(C_1 +α^j(C_2 +...+α^j(C_{n-2} +α^jC_{n-1})...))$



Ejemplo 2 . Deje que el vector de error tenga la forma = <0 0 0 0 12 0 0 0 0 0 0 8 0 0 0>. Destroza los caracteres en las posiciones 3 y 10 en el vector de código. Los valores de error son 8 y 12, respectivamente; estos valores también son elementos del campo GF (2 ⁴ ) y se dan en notación decimal (Tabla P). En el vector E, las posiciones están numeradas desde las inferiores de derecha a izquierda, comenzando desde 0 (1) 14.



Formemos ahora un vector de código con dos errores en el tercer bit y en el décimo con los valores 8 y 12, respectivamente. Esto se hace sumando el GF (2 ⁴) según las reglas aritméticas de este campo. Sumar elementos de campo con cero no cambia su valor. Los valores distintos de cero (elementos de campo) se suman después de convertirlos a una representación polinomial, ya que los polinomios generalmente se suman, pero los coeficientes para la incógnita se reducen mod 2.



Después de obtener el resultado de la suma, se vuelven a convertir a representación decimal, habiendo pasado previamente por la representación de potencia





A continuación se muestra el cálculo de valores corruptos por error en las posiciones 10 y 3 de la palabra de código:



$$$(7+12) →α^6+α^11 =x^3 +x^2 +x^3 +x^2 +x^1 =α^1 = 2,$

$$$(3 + 8) →α^2+ α^7 =x^2 +x^3 +x^1 + 1 =α^{12}=13.$



El decodificador realiza cálculos de acuerdo con la fórmula general para los componentes Sj, j = 1 (1) m. Aquí (en el modelo) usamos la relación$$$S=EH^t$, dado que especificamos (simulamos) en el programa nosotros mismos, los términos distintos de cero se obtienen solo para i = 3 e i = 10.





A continuación, mostraremos especialmente los cálculos de esta fórmula en forma expandida.

La matriz de verificación de la PC - código

Tan pronto como se formula el polinomio generador del código, es posible construir una matriz de verificación para las palabras de código, así como determinar el número de errores a corregir ( ver aquí, el decodificador ). Construyamos una matriz auxiliar [7 × 15], a partir de la cual se pueden obtener dos matrices de verificación de paridad diferentes: las primeras seis filas son una y las últimas seis filas son la otra.



La matriz en sí está formada de una manera especial. Las dos primeras líneas son obvias, la tercera línea y todas las siguientes se obtienen restando de la (segunda) línea anterior un segmento de números naturales 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 mod 15. Cuando ocurre un valor cero, se reemplaza con 15, los residuos negativos se convierten en positivos.





Cada matriz corresponde a su propio polinomio generador para la codificación sistemática y no sistemática.

Determinación de los coeficientes del polinomio sindrómico

Además, determinaremos los coeficientes del polinomio del síndrome para j = 1 (1) 6.

Con respecto a una palabra de código con longitud$$$n<q=p^r$Al llegar a la entrada del decodificador, suponemos que está distorsionado por errores.



Para identificar el vector de errores, necesita saber lo siguiente:

• el número de posiciones distorsionadas en la palabra de código
• $$$v≤v_{max}=0.5m$;
• números (posición) de posiciones distorsionadas en una palabra de código $$$ℓ_i: ℓ_i=0(1)n-1$;
• valores de distorsión $$$e_ℓ; e_ℓ∊GF(2^4)$...

¿Cómo se calcula y se utiliza más el vector de síndrome (polinomio) S? Su papel en la decodificación de palabras en clave es muy importante. Demostremos esto con una ilustración usando un ejemplo numérico.



Ejemplo 3 . (Cálculo de los componentes del vector síndrome$$$S_{<6>}$ )





entonces al final tenemos $$$S_{<6>}=(S_1,S_2,S_3,S_4,S_5,S_6)$= <8,13,7,13,15,15>



Para mayor consideración, presentamos nuevos conceptos. El valor$$$x_i = α^{ℓ_i}$se llamará un localizador de errores, aquí el símbolo de palabra de código distorsionado en la posición $$$ℓ_i$, α es un elemento primitivo del campo GF (2 ⁴ ).



El conjunto de localizadores de errores de una palabra de código específica se considera a continuación como los coeficientes del polinomio localizador de errores σ (z), raíces$$$z_i$ cuales son los valores $$$x_i ^{-1}$inverso a los localizadores.



Además, las expresiones$$$(1-zx_i)=0$desaparecer.



$$$σ(z) = (1-zx_1)(1-zx_2)...(1-zx_v) =σ_vz^v +σ_{v-1}z^{v-1} +...+σ_1z +σ_0$

siempre término libre de la ecuación siempre término libre de la ecuación $$$σ_0 =1$...

El grado del polinomio de los localizadores de errores es igual av - el número de errores y no excede el valor$$$v≤v_{max}=0.5m$...



Todos los caracteres distorsionados están en diferentes posiciones de la palabra, por lo tanto, entre los localizadores$$$x_i = α^i$, no puede haber elementos de campo repetidos y el polinomio σ (z) = 0 no tiene raíces múltiples.



Para facilitar la escritura, los valores de error se volverán a designar con el símbolo$$$Y_i = e_i$... Para los coeficientes del polinomio sindrómico, previamente se consideraron ecuaciones no lineales. En nuestro caso, v = 1 es el origen de los componentes del síndrome.





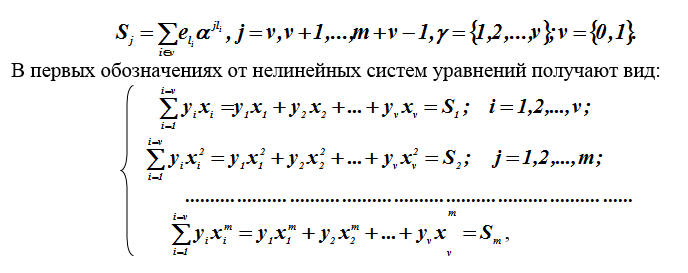
Dónde $$$y_i,x_i$ Son cantidades desconocidas, y $$$S_j$- parámetros conocidos, calculados en la primera etapa de decodificación (componentes del vector del síndrome).



Se desconocen los métodos para resolver tales sistemas de ecuaciones no lineales, pero las soluciones se encuentran usando trucos (soluciones alternativas). La transición al sistema de ecuaciones lineales de Hankel (Toeplitz) con respecto a los coeficientes$$$σ_i$el polinomio localizador.



Conversión a un sistema de ecuaciones lineales



A una ecuación$$$σ_i$ del polinomio del localizador de errores, el valor de sus raíces se sustituye $$$z =x_i^{-1}$... En este caso, el polinomio desaparece. Se forma una identidad, ambos lados de la cual se multiplican por$$$y_ix_i^{j+v}$, obtenemos:



$$$y_i(σ_vx_i^{j}+σ_{v-1}x_i^{j+1}+...+σ_1x_i^{j+v-1}+x_i^{j+v})=0,1≤i≤v, 1≤j≤v$...



Obtenemos tales igualdades$$$v×v =v^2$



Sumamos estas igualdades sobre todos $$$i, 1≤i≤v$por lo que se satisfacen estas igualdades. Dado que el polinomio σ (z) tiene v raíces$$$x_i^{-1}$, abre los corchetes y transfiere los coeficientes $$$σ_i$ por signo de la cantidad:





En esta igualdad, según el sistema de ecuaciones no lineales dado

anteriormente, cada suma es igual a uno de los componentes del vector de síndrome. De ahí que concluya que con respecto a los coeficientes$$$σ_v, σ_{v-1},...,σ_1$ puedes escribir un sistema de ecuaciones lineales.





Los signos "-" cuando se calcula sobre un campo binario se omiten, ya que corresponden a "+". El sistema resultante de ecuaciones lineales es Hankel y corresponde a una matriz con dimensiones$$$v×(v+1)$ poco.





Esta matriz no está degenerada si el número de errores en la palabra de código C (E) es estrictamente igual a $$$v , v ≤0.5(n-k)$, es decir la capacidad de inmunidad al ruido de este código no se viola.

Resolver un sistema de ecuaciones lineales

El sistema resultante de ecuaciones lineales contiene los coeficientes como incógnitas $$$σ_i =1(1)t$el polinomio del localizador de errores para la palabra clave C (E). Los componentes previamente calculados del vector del síndrome$$$S_j, j=1(1)m$... Aquí t es el número de errores en la palabra, m es el número de posiciones de verificación en la palabra.



Existen diferentes métodos para resolver el sistema formado.



Tenga en cuenta que la matriz (Hankel) no está degenerada para las dimensiones limitadas por el número de errores permitidos en una sola palabra (menos de 0,5 m). En este caso, el sistema de ecuaciones se resuelve de forma única y el problema se puede reducir simplemente a la inversión de la matriz de Hankel. Sería deseable eliminar la limitación sobre la dimensión de las matrices, es decir sobre un campo sin fin.



Los métodos para resolver el sistema de ecuaciones lineales de Hankel se conocen en campos infinitos:

• Trinchera iterativa - Berlekamp - método Messi (método TBM); (1)
• Peterson-Gorenstein-Zierler determinista directo; (PHC - método); (2)
• El método de Sugiyama utiliza el algoritmo de Euclid para encontrar GCD (método C). (3)

Sin considerar otros métodos, optaremos por el método TBM. La motivación para la elección es la siguiente.



El método (PHC) es simple y bueno, pero para un pequeño número de errores corregibles, el método C es difícil de implementar en una computadora y está publicado (cubierto) de manera limitada en las fuentes, aunque el método C, como el método TBM según el conocido polinomio de síndromes S (z), proporciona solución de la ecuación de Pade sobre el campo de Galois. Esta ecuación se forma para el polinomio de localizadores de error σ (z) y el polinomio ω (z), en teoría de codificación se llama ecuación clave de Pade:



$$$S(z)σ(z) = ω(z)(mod z^m)$...



La solución a la ecuación clave es el conjunto$$$x_i^{-1}$ raíces del polinomio σ (z) y, en consecuencia, los localizadores $$$x_i =α^{ℓ_i}$, es decir posiciones de error. Valores de error (magnitudes)$$$e_i$ se determinan a partir de la fórmula de Forney en la forma





Dónde $$$σ_z^{'}(α^{-i})$ y $$$ω(α^{-i})$ ¿Son los valores de los polinomios σ (z) y ω (z) en el punto $$$z =α^{-i}$inversa a la raíz del polinomio σ (z);

i es la posición del error;$$$σ_z^{'}(z)$ - la derivada formal del polinomio σ (z) con respecto a z;

Derivada formal de un polinomio en un campo finito

Existen diferencias y similitudes para la derivada con respecto a una variable en el campo de los números reales y la derivada formal en un campo finito. Considere el polinomio





$$$a_i$Son los elementos del campo, i = 1 (1) n



elementos del campo. Se proporciona un código sobre un campo real GF (2 ⁴ ). La derivada con respecto a z es:





En un campo real infinito, las operaciones se multiplican por ny suman n veces coinciden. Para campos finitos, la derivada se define de manera diferente.



La derivada se determina de manera similar por la relación:





donde ((i)) = 1 + 1 + ... + 1, (i) veces, sumadas de acuerdo con las reglas de un campo finito: el signo + denota la operación "sumar tantas veces", es decir elemento$$$a_2z$ repetir 2 veces, elemento $$$a_3z^2$ repetir 3 veces, elemento $$$a_nz^{n-1}$repetir n veces.



Está claro que esta operación no coincide con la operación de multiplicación en un campo finito. En particular, en los campos GF (2 ^r ), la suma de un número par de términos idénticos se toma mod2 y se pone a cero, y un número impar es igual al término en sí sin cambios. Por tanto, en el campo GF (2 ^r ), la derivada toma la forma





la segunda y más alta derivada par en este campo es igual a cero.



A partir del álgebra se sabe que si un polinomio tiene raíces múltiples (de multiplicidad p), entonces la derivada del polinomio tendrá la misma raíz, pero con multiplicidad p-1. Si p = 1, entonces f (z) y f '(z) no tienen raíz común. Por lo tanto, si un polinomio y su derivada tienen un divisor común, entonces hay una raíz múltiple. Todas las raíces de la derivada f '(z) son múltiplos en f (z).

Método de solución de ecuaciones clave

TMB (Trench-Berlekampa-Messi) es un método para resolver la ecuación clave. El algoritmo iterativo proporciona la definición de los polinomios σ (z) y ω (z), y la solución de la ecuación de Pade (clave).



Datos iniciales: coeficientes polinomiales$$$S_1,S_2,...,S_n$grado n-1.

Objetivo. Definición en forma explícita (analítica) de los polinomios σ (z) y ω (z).



El algoritmo utiliza la siguiente notación: j - número de paso,$$$v_j$ - el grado del polinomio, $$$σ_j(z) =σ_{ji}z^i +σ_{ji-1}z^{i-1}+...+σ_{j1}z+σ_{j0}$ - expansión del polinomio en potencias $$$z, k_j, L_j, θ_j(z)$ y $$$Ω_j(z)$- variables y funciones intermedias en el j-ésimo paso del algoritmo;



Deben especificarse las condiciones iniciales, ya que aquí se utiliza la recursividad.



Condiciones iniciales:





Ejemplo 4 . Ejecución del algoritmo iterativo para el vector

S = (8,13,7,13,15,15). Los polinomios están definidos$$$σ(z) =σ_n(z)$ y $$$ω(z) = ω_n(z)$...



Tabla 2 - Cálculo de polinomios localizadores de errores







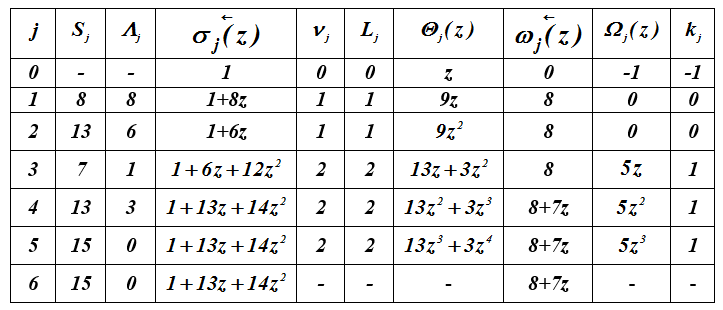
entonces $$$σ_j^←(z)=14z^2+13z+1$, $$$ω_j^←(z)$= 7z + 8.



El polinomio localizador de errores σ (z) sobre el campo GF (2 ⁴ ) con el polinomio irreducible p (x) = x ⁴ + x + 1 tiene raíces



$$$z_1 = α^{-i_1} = 13 = 4^{-1}$ y $$$z_2 =α^{-i_2} = 6 = 11^{-1}$, es fácil de verificar mediante verificación directa, es decir $$$i_1= 3, i_2 =10, 13 = α^{12}, 1 =α^{12}α^{3}$ y $$$α^{12} =α^{-3}=>13=4^{-1}$... Sustitución de raíces en

$$$σ(z=13)=14(13)^2+13·13+1=α^{13}(α^{12})^2+(α^{12})^2+α^0= α^{37}+α^{24} +α^{0}$=

=$$$α^{7}+α^{9}+α^0 =x^3+x+1=0(mod2)$;

$$$σ(z = 6)=14(6)^2+13·6+1 = α^{13}(α^{5})^2+(α^{5})^2+α^{0}$=

=$$$α^{8}+α^{2} +α^{0} = x^2 +1+x^2 +1 = 0(mod2)$...



Tomando la derivada formal de σ (z), obtenemos σ_2 (z) = 2 14 + 13 = 13, ya que 14z se toma en la suma 2 veces y desaparece mod 2.



Usando la fórmula de Forney, encontraremos expresiones para calcular los valores de error$$$e_i$...



Sustituyendo los valores i = 3 e i = 10 posiciones en la última expresión,

encontramos



$$$_3 = 10α^{15-3}+11 =α^{6}+α^{10}$= =$$$x^3+x^2+x^2+x+1=x^3+x+1=α^{7}=>8$;

$$$_{10} = 10α^{15-10}+11 =α^{9}α^{5}+α^{10}=α^{14}+α^{10}$= =$$$x^3+x^2+x=α^{11}=>12$...

La arquitectura de la construcción de un paquete de software

Para construir un paquete de software, se propone utilizar la siguiente solución arquitectónica. El paquete de software se implementa como una aplicación con una interfaz gráfica de usuario.



Los datos iniciales del paquete de software son un flujo de información digital descargado mediante un volcado de un archivo. Para la conveniencia del análisis y la claridad de la operación compleja, se supone que debe usar archivos .txt.



El flujo digital cargado se presenta en forma de matrices de datos, en el curso del trabajo complejo en el que se aplican diversas acciones computacionales.



En cada etapa de la operación compleja, es posible visualizar los resultados intermedios del trabajo.



Los resultados de la operación compleja del programa se presentan en forma de datos numéricos que se muestran en tablas.



Los resultados de los análisis intermedios y finales se guardan en archivos.



El esquema del funcionamiento del complejo de software La



operación con el complejo comienza con la carga del flujo digital usando el volcado del archivo. Una vez descargado, al usuario se le presenta una representación visual del contenido binario del archivo y su contenido textual.



En el marco de esta interfaz, se deben implementar las siguientes tareas funcionales:

• Descargue el mensaje original;
• Conversión de un mensaje en un volcado;
• Codificación de mensajes;
• Simulando un mensaje interceptado
• Construcción de espectros de las palabras de código recibidas para analizar su representación visual;
• Visualización de parámetros de código.

Descripción del funcionamiento del paquete de software



Cuando se inicia el archivo ejecutable del programa, aparece en la pantalla la ventana que se muestra en la Figura 2, que muestra la interfaz principal del programa.



La entrada del programa es un archivo que debe transmitirse por el canal de comunicación. Para su transmisión a través de canales de comunicación reales, se requiere codificación: la adición de símbolos de verificación, necesarios para la decodificación inequívoca de una palabra en la fuente-receptor. Para iniciar el complejo, debe seleccionar el archivo de texto requerido usando el botón "Cargar archivo". Su contenido se mostrará en el campo inferior de la ventana principal del programa.



La representación binaria del mensaje se presentará en el campo correspondiente, la representación binaria de palabras de información - en el campo “Representación binaria de palabras de información”.



El número de bits del mensaje original y el número total de palabras que contiene se muestran en los campos "Número de bits en el mensaje transmitido" y "Número de palabras en el mensaje transmitido".



La información formada y las palabras de código se muestran en tablas en el lado derecho de la ventana principal del programa.



La ventana del programa con resultados intermedios se muestra en la Figura 3.





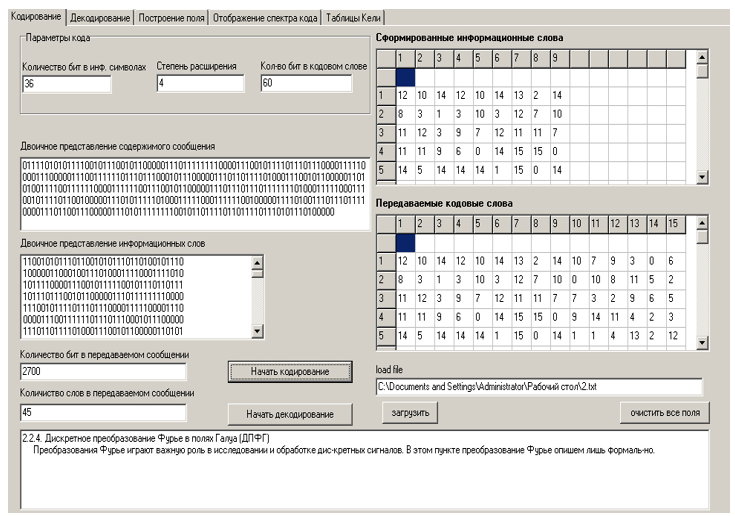
Figura 3 - Presentación intermedia de los resultados del paquete de software





Figura 4. Resultados de la descarga del archivo de mensaje





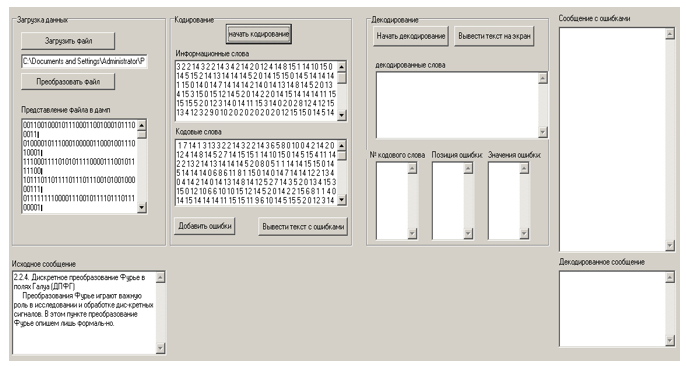
Figura 5. Resultados de la codificación de archivos





Figura 6. Salida de un mensaje con errores ingresados.





Figura 7. Salida de los resultados de la decodificación y del mensaje con errores introducidos





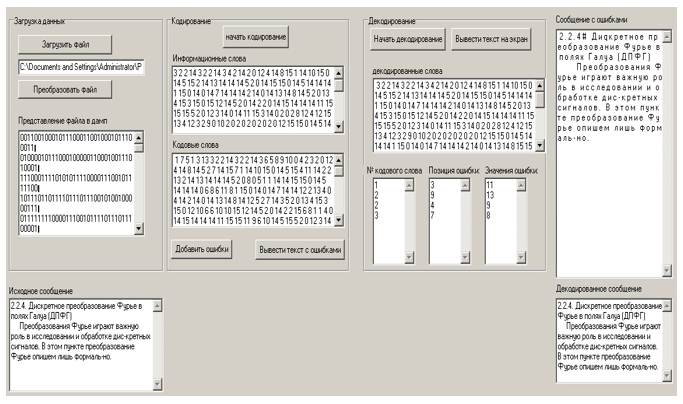
Figura 8. Salida del mensaje decodificado.

Conclusión

La NSA de EE. UU. Es el operador principal del sistema de interceptación global Echelon. Echelon tiene una amplia infraestructura que incluye estaciones de seguimiento en tierra ubicadas en todo el mundo. Se supervisan casi todos los flujos de información del mundo.



El estudio de las posibilidades de acceder a la semántica de los mensajes de información codificados en el momento actual de la guerra de información activa tanto en el campo de la tecnología como en la política se ha convertido en un desafío más y una de las tareas urgentes y demandadas de nuestro tiempo.



En la inmensa mayoría de los códigos, la codificación y decodificación de mensajes (información) se implementa sobre una base matemática rigurosa de campos de Galois extendidos finitos. Trabajar con elementos de tales campos difiere de los generalmente aceptados en aritmética y requiere escribir procedimientos especiales para manipular elementos de campo cuando se utilizan herramientas computacionales.

El trabajo ofrecido a la atención de los lectores abre levemente el velo del secreto sobre tales actividades a nivel de firmas, empresas y estados en general.