Curvas circulares de segundo orden

Como sabe , las curvas de Bézier no pueden construir un arco de círculo o una elipse. Este artículo analiza las curvas que no tienen esta desventaja.

Curvas de Bezier

La lógica detrás de la construcción de las curvas de Bezier se comprende bien en la siguiente animación:







Para obtener la fórmula directamente de la representación gráfica, basta con definir una función auxiliar para la interpolación lineal entre dos puntos, en la cual, cuando el parámetro t cambia de 0 a 1, devuelve valores intermedios de a a b :

$$

$$mix(a,b,t) =a (1-t)+b t$$

Con su ayuda, puede encontrar constantemente los puntos necesarios: primero encuentre

$$

$$ac = mix(a, c, t)$$

y

$$

$$cb = mix(, b, t)$$

y luego a través de ellos encontrar

$$

$$d = mix(ac, cb, t)$$

Si lo desea, puede sustituir las funciones entre sí y acortar, aunque esto no simplificará particularmente los cálculos, le permitirá generalizar las curvas a un número arbitrario de puntos de control (a través de polinomios de Bernstein). En nuestro caso, obtenemos

$$

$$d = a (1-t)^2+b t^2+2 c t (1-t)$$

El aumento del orden de las curvas se logra de manera trivial: los puntos de origen no se establecen constantes, sino como resultado de la interpolación entre n + 1 otros puntos de control:

Curvas circulares

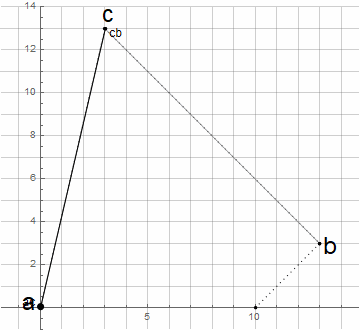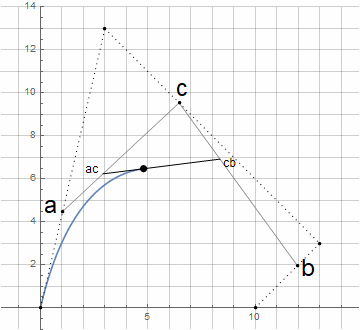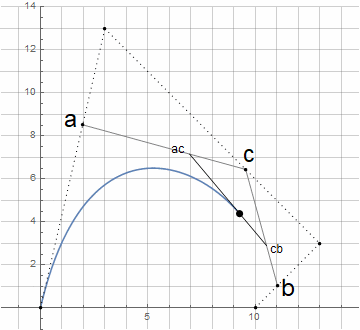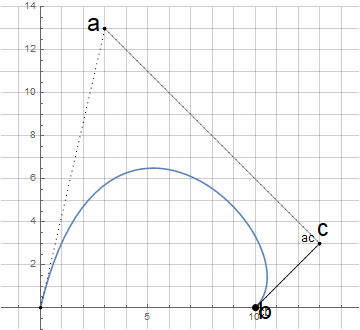
Arco de círculo

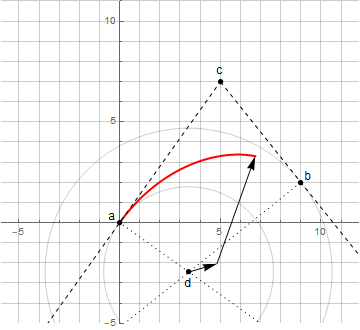
Para construir un arco circular de manera similar, es necesario determinar la lógica de construcción adecuada, por analogía con el dibujo de un círculo con una brújula.





Inicialmente, no sabemos el centro del círculo d - que se encuentra a través de la intersección de las perpendiculares a las tangentes en los puntos a y b (en adelante nodal); las propias tangentes se especifican mediante el punto c (en lo sucesivo, la directriz). Para crear un arco circular arbitrario (menos de 180 °), es suficiente que las distancias desde el punto de dirección a los puntos nodales sean las mismas.

Arco de elipse

Construir un arco de elipse ya es más difícil: necesita dos vectores girando en diferentes direcciones ( más detalles aquí )





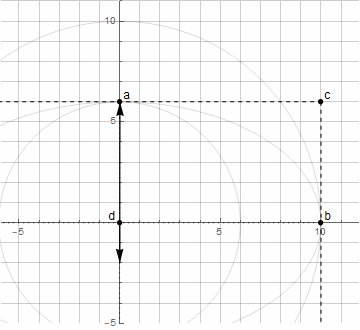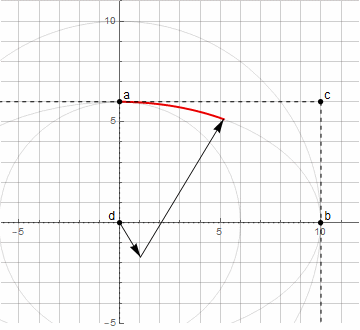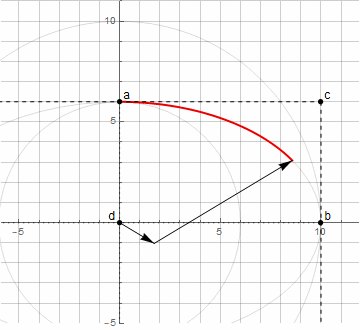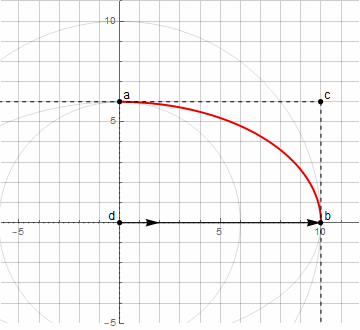
Usando el método anterior para encontrar el punto d , ya no podemos construir un arco arbitrario de una elipse, solo de 0 ° a 90 ° (incluido el giro en un cierto ángulo).

Arco hipotrocoide

Estableciendo la condición de que al principio y al final del dibujo los vectores deben estar en una línea recta, obtenemos el arco del hipotrocoide en todos los demás casos. Esta condición no es accidental y (además de la definición única de la curva) garantiza la coincidencia de las tangentes en los puntos nodales. Como consecuencia, las trayectorias angulares que recorren ambos vectores serán diferentes, pero aun así suman 180 °.





Cómo cambia la forma de la curva según la posición del punto guía se puede ver en la siguiente animación:

Algoritmo

Dado que aquí tenemos rotaciones en un plano bidimensional, es conveniente describir las matemáticas de construir estas curvas en términos de números complejos.



1) encuentre el punto de intersección de las normales de las tangentes trazadas desde el punto de dirección a los puntos nodales:

$$

$$d=\frac{(2 a-c) (c-b) a^*+ (2 b-c) (a-c) b^*-c (a-b) c^*}{(c-b)a^*+(a-c) b^*-(a-b) c^*}$$

(aquí el asterisco significa conjugación compleja).



2) conociendo d , encontramos las longitudes de las normales

$$

$$r_{\text{ad}}=\left| a-d\right|$$

$$

$$r_{\text{bd}}=\left| b-d\right|$$

y su suma y diferencia

$$

$$r_m=\frac{1}{2} \left(r_{\text{ad}}+r_{\text{bd}}\right)$$

$$

$$r_s=\frac{1}{2} \left(r_{\text{ad}}-r_{\text{bd}}\right)$$

3) encuentra el vector unitario a partir del cual comienza la construcción

$$

$$v=\frac{a-d}{\left| a-d\right| }$$

4) encuentra las trayectorias angulares que debe pasar cada uno de los vectores

$$

$$\phi _m=\arg \left(\frac{a-d}{b-d}\right)$$

$$

$$\phi _s=\arg \left(-\frac{a-d}{b-d}\right)$$

5) cambiando sucesivamente t de 0 a 1 con algún paso, encontramos el punto que pertenece a la curva por la fórmula

$$

$$d+v \left(r_m e^{-i t \phi _m}+r_s e^{-i t \phi _s}\right)$$

Splines circulares

Al igual que las curvas de Bézier, estas curvas se pueden combinar para crear splines continuos por partes. Para garantizar la suavidad en los puntos de anclaje (atraque), el punto de anclaje debe estar alineado con dos puntos de dirección adyacentes. Para hacer esto, puede especificar puntos de ancla no explícitamente, sino a través de la interpolación de los puntos de dirección. Tampoco se pueden especificar en absoluto, calculando de forma completamente automática, por ejemplo, como el promedio entre los puntos guía: a







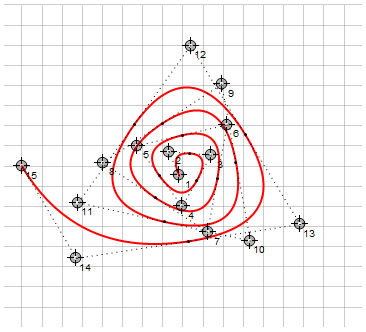
la derecha, para comparar, se utilizó el mismo enfoque con las curvas de Bézier de segundo orden.

Notas y matices

A diferencia de las curvas de Bézier, aquí la curva no siempre se encuentra dentro de la forma de las líneas que conectan los puntos de control, por ejemplo





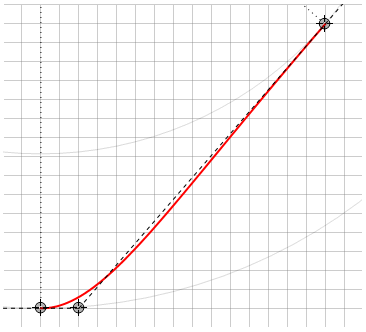
Además, existe un caso degenerado que debe manejarse por separado, cuando el punto de dirección se encuentra en la misma línea que los puntos de anclaje. En este caso, la curva degenera en una línea recta, y al intentar calcular el punto d , se produce la división por cero.



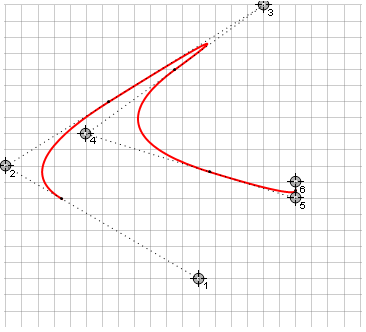
Estas curvas también tienen restricciones en la curvatura de la línea, porque el algoritmo elige la ruta más pequeña a seguir y la curva no puede dar más de 180 °. Esto lleva al hecho de que con la interpolación continua por partes, pueden ocurrir esquinas afiladas en una determinada posición de los puntos de dirección (a la derecha, los mismos puntos para Bezier):

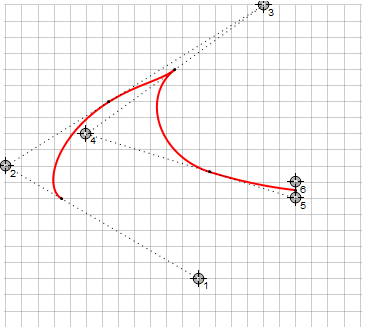
Conclusión

Un mayor desarrollo del método considerado para construir curvas es un aumento en el número de vectores involucrados en la construcción de la curva y, en consecuencia, un aumento en el número de puntos de dirección. Sin embargo, a diferencia de las curvas de Bezier, aumentar el orden aquí no es obvio y requiere una reflexión cuidadosa por separado. También son posibles varios métodos para combinarlos con las curvas de Bezier, en particular, la interpolación del centro del círculo de los vectores de dibujo.



El método considerado para construir curvas tampoco es el único, un caso especial de los cuales son los arcos de un círculo y una elipse; al menos se puede construir una elipse a través de la intersección de líneas rectas en un paralelogramo.(sin embargo, en esta versión el autor ha fallado). Es posible que haya otras soluciones, incluidas las opciones descritas en el artículo; escriba en los comentarios si sabe algo sobre este tema.



El código fuente del artículo se puede descargar de GitHub .