Al traducir la hipótesis de Keller a un lenguaje de búsqueda de gráficos comprensible por computadora, los investigadores finalmente resolvieron el problema de cubrir espacios con mosaicos.

Un equipo de matemáticos finalmente ha descubierto la hipótesis de Keller, pero no por sí mismos. En cambio, entrenaron a toda una flota de computadoras y lo resolvieron.
La hipótesis de Keller, planteada hace 90 años por Ott-Heinrich Keller, está relacionada con la tarea de cubrir espacios con mosaicos idénticos. Ella sostiene que si pavimenta un espacio bidimensional con baldosas cuadradas bidimensionales, al menos dos de ellas tendrán que tocar los lados por completo, y no parcialmente. La hipótesis hace la misma predicción para cualquier dimensión, es decir, cuando se llena un espacio de 12 dimensiones con "cuadrados" de 12 dimensiones, al menos dos de ellos deben tener un borde común.
Durante años, los matemáticos se pelearon por esta hipótesis, demostrando su verdad para algunas dimensiones y falsa para otras. Y para el otoño pasado, la cuestión seguía sin resolverse solo para el espacio de siete dimensiones.
Pero la nueva evidencia generada por computadora también resolvió ese problema. La prueba , publicada el pasado mes de octubre, es uno de los ejemplos más recientes de la combinación del genio humano y el poder informático puro para responder a las preguntas más interesantes de las matemáticas.
Los autores del nuevo trabajo, Joshua Breukensik de Stanford, Marin Hijul y John Mackey de la Universidad Carnegie Mellon, y David Narvaez del Instituto de Tecnología de Rochester, resolvieron este problema utilizando 40 computadoras. En apenas 30 minutos, las máquinas dieron una respuesta monosilábica: sí, en siete dimensiones, la hipótesis es correcta. Y ni siquiera tenemos que tomar esta conclusión por fe.
Adjunto a la respuesta hay una gran evidencia que explica su verdad. La prueba es demasiado larga para que la comprenda un humano, pero otro programa de computadora puede verificarla.
En otras palabras, incluso si no sabemos exactamente qué hicieron las computadoras para probar la hipótesis de Keller, al menos podemos asegurarnos de que lo hicieron bien.
La misteriosa séptima dimensión
Es fácil ver que la conjetura de Keller es cierta en dos dimensiones. Toma un trozo de papel e intenta cubrirlo con cuadrados iguales sin espacios ni superposiciones. Muy pronto te darás cuenta de que solo puedes hacer esto si al menos dos cuadrados tienen el mismo lado. Si tiene cubos a mano, le resultará fácil verificar que la hipótesis sea cierta para la tercera dimensión. En 1930, Keller sugirió que esta relación funciona para todas las dimensiones y sus correspondientes mosaicos.
Los primeros resultados apoyaron la predicción de Keller. En 1940, Oscar Perron demostró que la hipótesis era correcta para las mediciones del uno al seis. Sin embargo, más de 50 años después, una nueva generación de matemáticos encontró el primer contraejemplo de esta hipótesis: en 1992, Jeffrey Lagarias y Peter Shoredemostró que la hipótesis no funciona en la décima dimensión.

La hipótesis de Keller predice que al llenar un espacio en cualquier dimensión, al menos dos fichas deben tocar completamente los lados.
Al llenar un espacio bidimensional, muchos mosaicos tienen lados comunes (líneas azules).
Al llenar el espacio 3D, muchos cubos tienen caras comunes (azul).
Es fácil demostrar que si una hipótesis falla en alguna dimensión, no se sostiene en todas las superiores. Por lo tanto, después del trabajo de Lagarias y Shor, solo queda resolver el tema de la séptima, octava y novena dimensión. En 2002, Mackey demostró que la hipótesis de Keller era falsa para la dimensión ocho (y por lo tanto, nueve).
Solo la séptima dimensión permaneció abierta: era la dimensión más grande para la que esta hipótesis es cierta o la más pequeña en la que la hipótesis es incorrecta.
"Nadie sabe exactamente qué está pasando allí", dijo Khiyul.
Conecta los puntos
Si bien los matemáticos lucharon con este problema durante varias décadas, sus métodos cambiaron gradualmente. Perron trabajó en las primeras seis dimensiones usando solo lápiz y papel, pero en la década de 1990 los investigadores habían descubierto cómo traducir la hipótesis de Keller a una forma completamente diferente, permitiéndoles usar computadoras para resolverla.
La formulación original de la conjetura de Keller se refiere al espacio continuo uniforme. En un espacio así, hay un número infinito de formas de colocar un número infinito de fichas. Pero las computadoras no son buenas para resolver problemas con un número infinito de opciones; para hacerles frente, necesitan objetos discretos y finitos.

Marin Hijul de la Universidad Carnegie Mellon
En 1990, Kereszteli Korradi y Sandor Shabo idearon un objeto discreto adecuado. Demostraron que se pueden formular preguntas equivalentes a la hipótesis de Keller sobre este objeto. Y si prueba algo relacionado con estos objetos, entonces se probará la hipótesis de Keller. Esto redujo la cuestión del infinito a un problema aritmético menos complejo con múltiples números.
Así es como funciona.
Supongamos que quiere tratar la hipótesis de Keller en dos dimensiones. Corradi y Chabot idearon un método para esto, utilizando la construcción de una estructura, a la que llamaron gráfico de Keller.
Para empezar, imagina que hay 16 dados sobre la mesa, y todos tienen un borde superior con dos puntos (dos puntos denotan un espacio bidimensional y por qué hay 16 cubos, lo veremos un poco más adelante). Todos los cubos se rotan de la misma forma, de modo que los dos puntos se ubiquen igual para todos. Colorea cada punto con cualquiera de los cuatro colores: rojo, verde, blanco o negro.
Los puntos en un cubo no cambian de lugar; deje que uno de ellos denote la coordenada xy el otro, y. Habiendo coloreado los cubos, comenzaremos a dibujar líneas, o aristas, entre pares de cubos si se cumplen dos condiciones: los puntos en el mismo lugar para un par de cubos tienen diferentes colores, y en el otro son diferentes y emparejados, y el rojo y el verde se consideran pares, o negro. con blanco.
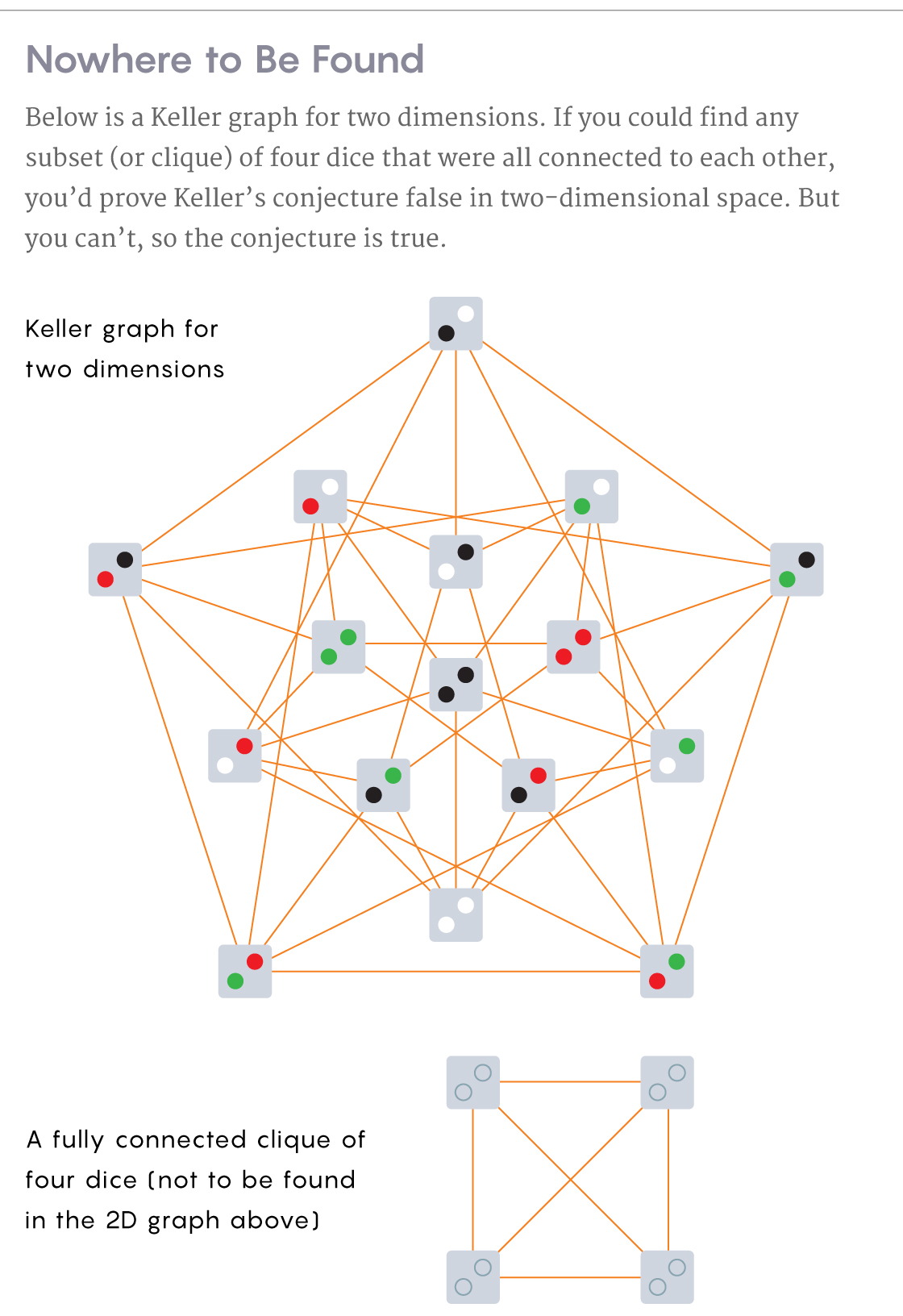
Gráfico de Keller para dos dimensiones. Al encontrar un subconjunto de cuatro cubos en los que cada uno está conectado a todos los demás, refutará la hipótesis de Keller para el espacio bidimensional. Sin embargo, no existe tal subconjunto y la hipótesis es correcta.
A continuación se muestra un ejemplo de una camarilla de cuatro dados completamente fusionada que no está en el gráfico.
Es decir, por ejemplo, si un cubo tiene dos puntos rojos y el otro dos puntos negros, no están conectados por un borde. Sus puntos en las mismas posiciones tienen colores diferentes, pero no satisfacen el requisito de emparejar colores. Si un cubo tiene puntos rojos y negros, y el otro tiene dos puntos verdes, están conectados por un borde, ya que en una posición tienen colores emparejados (rojo y verde), y en la otra son simplemente diferentes (negro y verde).
Hay 16 formas de colorear dos puntos con cuatro colores (por eso tenemos 16 cubos). Exponga todas estas 16 posibilidades frente a usted. Conecte todos los pares de cubos que satisfagan los requisitos. ¿Hay cuatro cubos en su esquema, cada uno de los cuales se combina con otros tres?
Este subconjunto de cubos completamente conectado se llama camarilla. Si puede encontrar uno, refutará la hipótesis de Keller en dos dimensiones. Sin embargo, no puede, simplemente no existe. Y la ausencia de tal camarilla de cuatro cubos significa que la hipótesis de Keller es cierta para dos dimensiones.
Estos cubos no son literalmente los mismos mosaicos que la hipótesis de Keller, sin embargo, puede asumir que cada cubo representa un mosaico. Considere los colores asignados a los puntos como las coordenadas que colocan al cubo en el espacio. Y la existencia de un borde es una descripción de cómo se colocan dos cubos entre sí.
Si los colores de los cubos son iguales, representan fichas que están igualmente espaciadas en el espacio. Si no tienen colores y pares de colores comunes (uno tiene blanco y negro, el otro tiene verde y rojo), indican mosaicos parcialmente superpuestos, lo que no está permitido para llenar el espacio. Si dos cubos tienen un conjunto de colores coincidentes y un conjunto del mismo color (uno rojo-negro, el otro verde-negro), representan fichas con un lado común.
Finalmente, y lo más importante, si tienen un conjunto de colores emparejados y otro conjunto de colores diferentes, es decir, si están conectados por un borde, entonces los cubos representan mosaicos que están en contacto entre sí, pero ligeramente desplazados, debido a que sus bordes no coinciden completamente. ... Es esta condición la que debemos estudiar. Los cubos conectados por un borde denotan fichas contiguas que no tienen un lado común; esta es la disposición que se necesita para refutar la hipótesis de Keller.
“Deben tocarse, pero no del todo”, dijo Khiyul.

Misma coloración, misma disposición.
Diferentes colores, sin pares, superpuestos.
Dos colores emparejados y un par del mismo son el lado común.
Dos colores emparejados y dos diferentes - contacto parcial por los lados.
Escalada
Hace treinta años, Corradi y Schabo demostraron que los matemáticos podían usar un procedimiento similar para trabajar con la hipótesis de Keller en cualquier dimensión, ajustando los parámetros del experimento. Para probar la hipótesis de Keller en tres dimensiones, puede usar 216 cubos con tres puntos en el borde y posiblemente tres pares de colores (sin embargo, aquí hay cierta flexibilidad). Luego debe buscar ocho cubos (2 3 ), completamente conectados entre sí, de acuerdo con las mismas condiciones que le dimos anteriormente.
En general, para probar la conjetura de Keller en n dimensiones, es necesario utilizar cubos con n puntos e intentar encontrar una camarilla de tamaño 2 n entre ellos . Se puede suponer que representa una especie de super-mosaico (que consta de 2 nmosaicos más pequeños) capaces de cubrir todo el espacio n-dimensional.
Si puede encontrar este super mosaico (que no tiene mosaicos con un lado común), puede usar copias de él para cubrir todo el espacio con mosaicos sin un lado común, lo que refutará la hipótesis de Keller.
“Si tiene éxito, puede cubrir todo el espacio con transferencia. Un bloque sin lados de baldosas comunes se extenderá a todo el piso ”, dijo Lagarias, ahora en la Universidad de Michigan.
Mackey refutó la hipótesis de Keller en la octava dimensión, encontrando una camarilla de 256 cubos (2 8 ), por lo que quedó para lidiar con la hipótesis en la 7ma dimensión, encontrando una camarilla de 128 cubos (2 7). Encontrar esta camarilla refutará la hipótesis de Keller en la séptima dimensión. Demuestre que no existe y probará que la hipótesis es cierta.
Desafortunadamente, encontrar un grupo de 128 cubos es una tarea especialmente difícil. En trabajos anteriores, los investigadores aprovecharon que las dimensiones 8 y 10 pueden, en cierto sentido, "descomponerse" en espacios de menor dimensión, con los que es más fácil trabajar. Y aquí esto no funcionó.
“La séptima dimensión es inconveniente porque 7 es un número primo y no se puede dividir en dimensiones de un orden más pequeño”, dijo Lagarias. "Por lo tanto, no había otra salida que lidiar con la combinatoria completa de estos gráficos".
Encontrar una camarilla de 128 cubos puede ser un desafío para el cerebro sin ayuda, pero este es el tipo de preguntas que las computadoras responden bien, especialmente con un poco de ayuda.
El lenguaje de la lógica
Para convertir la búsqueda de clics en una tarea que pueda manejar una computadora, debe formularla en términos de lógica proposicional . Este es un razonamiento tan lógico, que incluye un conjunto de restricciones.
Digamos que ustedes tres están planeando una fiesta con amigos. Está intentando crear una lista de invitados, pero hay conflictos de intereses. Digamos que quiere invitar a Alexei o excluir a Kolya. Uno de tus amigos quiere invitar a Kolya, a Vlad oa ambos. Otro amigo no quiere llamar ni a Alexei ni a Vlad. Con tales restricciones, ¿es posible crear una lista de invitados que satisfaga a los tres?
En términos de informática, este problema se denomina problema de aceptabilidad. Se puede resolver describiendo la condición en la fórmula proposicional. En este caso, se ve como sigue, y A, K y B denotan invitados potenciales: (A O NO K) Y (K O B) Y (NO A O NO B).
La computadora lo calcula sustituyendo 0 o 1. En cada variable, 0 es el valor de la variable "falso" o desactivado, y 1 es "verdadero" o activado. Sustituyendo 0 en lugar de A, decimos que Alexei no fue invitado y 1 que fue invitado. En esta fórmula simple, 0 y 1 se pueden sustituir (haciendo una lista de invitados) de muchas formas, y es posible que después de revisarlas toda la computadora concluya que no se pueden satisfacer todos los intereses. Sin embargo, en este caso, hay dos formas de sustituir 1 y 0 para complacer a todos: A = 1, K = 1, B = 0 (invita a Alexey y Kolya) y A = 0, K = 0, B = 1 (invita a un Vlad ).
El programa de computadora que resuelve tales declaraciones se llama solucionador SAT, donde SAT es la abreviatura de satisfacibilidad. Examina todas las combinaciones de variables y da una respuesta monosilábica, ya sea SÍ, hay una manera de satisfacer los requisitos de la fórmula, o NO, no lo es.

John Mackie de la Universidad Carnegie Mellon
"Solo está buscando para ver si puede asignar valores verdaderos y falsos a todas las variables para que toda la fórmula sea verdadera, y si es así, entonces es satisfactoria, y si no, entonces no", dijo Thomas Hales de Universidad de Pittsburgh.
La cuestión de encontrar un grupo de 128 cubos es un problema similar. También se puede reescribir como una fórmula proposicional y entregarse al solucionador de SAT. Comience con muchos cubos con 7 puntos cada uno y 6 colores posibles. ¿Es posible colorear los puntos para que 128 cubos estén conectados entre sí de acuerdo con ciertas reglas? En otras palabras, ¿es posible asignar colores para que aparezca el clic?
La fórmula proposicional para la pregunta seleccionada es bastante larga y contiene 39.000 variables. A cada uno se le puede asignar uno de dos valores, 0 o 1. Como resultado, el número de opciones posibles para organizar valores, o formas de asignar colores, fue 2,39,000 , que es muchísimo.
Para encontrar la respuesta a la pregunta sobre la hipótesis de Keller en siete dimensiones, la computadora tendría que verificar todas estas combinaciones, y excluirlas todas (lo que significaría que la camarilla del tamaño 128 no existe, y la hipótesis de Keller en la séptima dimensión es correcta), o encontrar al menos sería una opción de trabajo (refutando la hipótesis de Keller).
"Si hace una iteración simple de todas las posibilidades, se encuentra con un número de 324 dígitos", dijo Mackey. La computadora más rápida del mundo funcionaría hasta el fin de los tiempos, pasando por todas las posibilidades.
Sin embargo, los autores del nuevo trabajo descubrieron cómo una computadora puede dar una respuesta definitiva sin verificar todas las posibilidades. La clave de esto es la eficiencia.
Eficiencia oculta
Mackey recuerda el día en que, desde su punto de vista, el proyecto realmente empezó a funcionar. Estaba parado frente a una pizarra en su oficina en la Universidad Carnegie Mellon, discutiendo un tema con dos coautores, Hijul y Breikensik, cuando Hijul propuso una forma de estructurar la búsqueda para que pudiera completarse en un tiempo razonable.
"Había un verdadero genio humano trabajando en mi oficina ese día", dijo Mackey. - Era como ver a Wayne Gretzky o LeBron James en las Finales de la NBA. Se me pone la piel de gallina solo por el recuerdo ".
Puede personalizar las búsquedas para un gráfico de Keller específico de diferentes maneras. Imagina que tienes muchos cubos en tu mesa y estás tratando de resolver 128 de ellos, siguiendo las reglas del Conde Keller. Digamos que ha seleccionado 12 correctamente, pero no sabe cómo agregar el siguiente. En este punto, puede descartar cualquier configuración de 128 dados que incluya esta configuración no funcional de 12.
“Si sabe que sus cinco primeras asignaciones no coinciden, no necesita buscar otras variables, y esto generalmente reduce mucho el campo de búsqueda”, dijo Shore, ahora en MIT.
Otro tipo de eficiencia está asociado con la simetría. Los objetos simétricos son algo iguales. La identidad nos permite comprender el objeto completo como un todo, estudiando solo una parte de él; al mirar la mitad del rostro de una persona, puede restaurarlo por completo.
De manera similar, puede cortar esquinas en el caso de los gráficos de Keller. Imagina de nuevo que estás tratando de alinear los cubos sobre la mesa. Digamos que comienzas en el centro de la mesa y construyes tu mano a la izquierda. Coloca cuatro dados y llega a un callejón sin salida. Ahora ha eliminado una combinación inicial y todas las combinaciones basadas en ella. Sin embargo, puede excluir la duplicación de esta combinación inicial: la configuración de los cubos que obtiene si los coloca de la misma manera, solo a la derecha.
“Si se le ocurrió una manera de resolver problemas satisfactorios que tenga en cuenta la simetría de manera inteligente, habrá simplificado enormemente la tarea”, dijo Hales.
Cuatro colegas aprovecharon las eficiencias de esta búsqueda de una manera nueva: en particular, automatizaron la consideración de casos simétricos, mientras que los matemáticos los procesaban anteriormente casi a mano.
Como resultado, mejoraron su búsqueda de camarillas de tamaño 128 tanto que en lugar de verificar 2,39,000 configuraciones, su programa tuvo que verificar solo alrededor de mil millones ( 2,30 ). Esto hizo una búsqueda que podría llevar una eternidad en una tarea durante una mañana. Finalmente, después de solo media hora de cálculos, recibieron una respuesta.
“Las computadoras dijeron que no, así que sabemos que la hipótesis funciona”, dijo Hiyul. Es imposible colorear los 128 cubos para que se fusionen entre sí, por lo que se confirma la hipótesis de Keller para la séptima dimensión. Para cualquier colocación de baldosas que cubran un espacio, inevitablemente habrá al menos un par de bordes que se tocan completamente.
La computadora no solo dio una respuesta monosilábica. Le adjuntó una larga prueba de 200 GB que respalda esta conclusión.
La prueba no es solo un cálculo de todos los conjuntos de variables que han sido verificados por una computadora. Este es un argumento lógico que prueba que la camarilla necesaria no puede existir. Los investigadores introdujeron la evidencia en un programa que prueba la evidencia formal rastreando la lógica del argumento y la validaron.
“No solo revisamos todas las opciones y no encontramos nada. Revisamos todas las opciones y pudimos escribir pruebas de que tal cosa no existe ”, dijo Mackey. "Pudimos registrar la evidencia de insatisfacción".