Los físicos han encontrado la estructura algebraica que subyace a las intrincadas matemáticas de las colisiones de partículas. Algunos esperan que nos lleve a una teoría más elegante del mundo físico.
Cuando los físicos de partículas intentan modelar experimentos, se enfrentan a cálculos imposibles debido a una ecuación infinitamente grande que está fuera del alcance de las matemáticas modernas.
Afortunadamente, pueden hacer predicciones generalmente precisas sin trabajar con todas estas matemáticas crípticas hasta el final. Acortando los cálculos, los científicos del Gran Colisionador de Hadrones en el CERN, Europa, hacen predicciones que coinciden con los eventos que luego observan en colisiones de partículas subatómicas que se desplazan a una velocidad tremenda a lo largo de una pista de 26 kilómetros.
Desafortunadamente, la era del acuerdo entre la predicción y la observación puede estar llegando a su fin. Cuanto más precisas se vuelven las mediciones, más difícil es mantener el ritmo de los esquemas de cálculo aproximado utilizados por los teóricos.
“Ya estamos cerca de agotar los fondos que tenemos”, dijo Claude Dar , físico de partículas del CERN.
Sin embargo, tres trabajos recientes de Pierpaolo Mastrolia de la Universidad de Padua en Italia y Sebastian Mizeradel Instituto de Estudios Avanzados de Princeton en Nueva Jersey descubrió la estructura matemática detrás de estas ecuaciones. Proporciona una nueva forma de colapsar un número infinito de miembros en una docena de componentes necesarios. Su método puede ayudar a llevar la precisión de la predicción al siguiente nivel que los teóricos necesitan para ir más allá del modelo principal pero incompleto de la física de partículas.
“Han mostrado muchos resultados que demuestran la viabilidad de esta técnica prometedora”, dijo Dar.
Sin embargo, los beneficios pueden ser mucho mayores que simplemente mejorar las predicciones. El nuevo método evita las aburridas matemáticas tradicionales al calcular directamente los "números de intersección", que algunos creen que, en última instancia, pueden darnos una descripción más elegante del mundo subatómico.
"No se trata sólo de matemáticas", dijo Simon Caron-Hewot de la Universidad McGill, un teórico cuántico que estudia las implicaciones del trabajo de Mastrolius y Mizera. "Todo está profundamente entrelazado con la teoría cuántica de campos".
Bucle infinito
Al modelar colisiones de partículas, los físicos usan diagramas de Feynman , una notación simple inventada por Richard Feynman en la década de 1940.
Para comprender cómo funciona esta grabación, considere un evento simple: dos quarks se acercan, intercambian un gluón en el proceso de "colisión" y luego rebotan entre sí a lo largo de diferentes trayectorias.
En el diagrama de Feynman, las trayectorias de los quarks se indican mediante "patas", que forman "cimas" en la unión durante la interacción de partículas. Feynman desarrolló reglas para convertir esa imagen en ecuaciones que calculan la probabilidad de que ocurra este evento. Escribe una función específica para cada cateto y vértice, generalmente una fracción usando la masa y el momento de la partícula, y lo multiplica todo. Para opciones simples como la nuestra, los cálculos pueden caber en una servilleta.
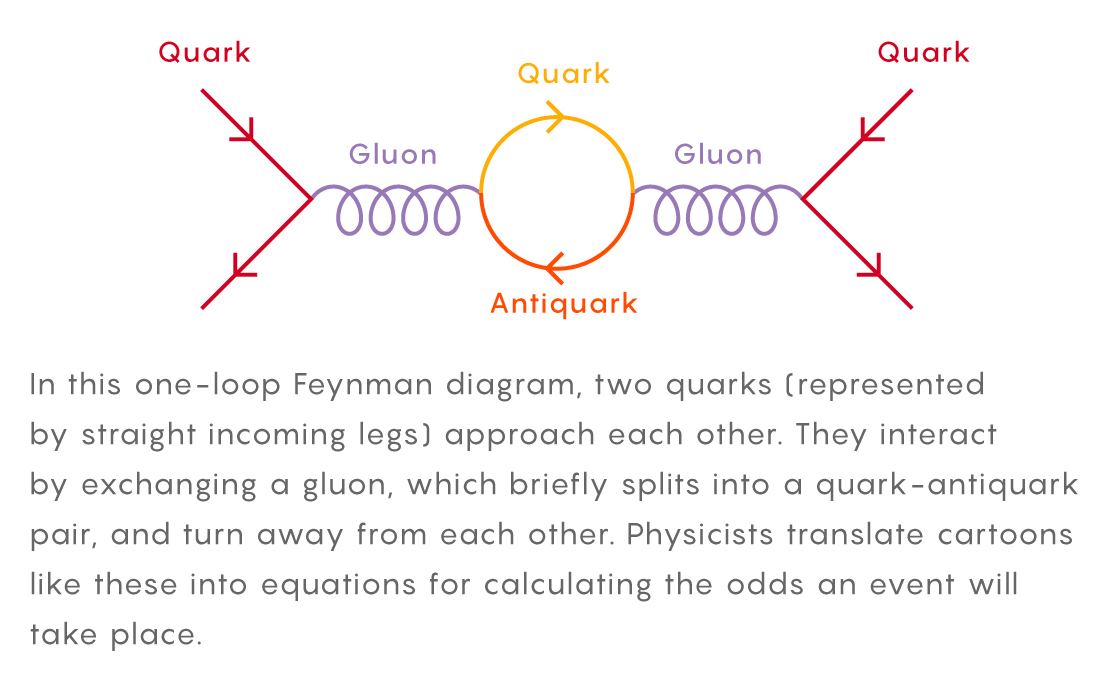
En este diagrama, dos quarks (indicados por patas rectas con flechas apuntando hacia adentro) se acercan a un bucle. Interactúan, intercambiando gluones, que durante un corto período de tiempo se dividen en un par quark-antiquark, y luego se separan. Los físicos traducen estos patrones en ecuaciones que calculan la probabilidad de que ocurra este evento.
Sin embargo, la regla de oro de la teoría cuántica es considerar todas las posibilidades, y el intercambio de un gluón simple es solo uno de la gran variedad de escenarios que pueden desarrollarse cuando dos quarks chocan. El gluón que intercambian las partículas se puede dividir en un par de quark-antiquark durante un corto período de tiempo y luego volver a convertirse en un gluón. Dos quarks se encuentran y dos quarks divergen, pero pueden suceder muchas cosas en el medio. Para explicar completamente lo que está sucediendo, dando una predicción ideal, necesitará dibujar un número infinito de diagramas. Nadie espera resultados perfectos, pero la clave para mejorar la precisión de los cálculos es llegar lo más lejos posible a lo largo de la interminable cadena de eventos.
Y aquí es donde los físicos se atascan.
Para estudiar este centro oculto con más detalle, debe recurrir a las partículas virtuales, fluctuaciones cuánticas que afectan gradualmente el resultado de cada interacción. La existencia a corto plazo del par de quarks mencionado anteriormente, como muchos eventos virtuales, se indica en el diagrama de Feynman mediante un circuito cerrado. Los bucles desconciertan a los físicos: son cajas negras que agregan capas adicionales a escenarios infinitos. Para calcular de alguna manera las posibilidades implícitas en el ciclo, los teóricos deben tomar integrales. Estas integrales alcanzan proporciones monstruosas en los diagramas de Feynman, con muchos bucles que aparecen a medida que los investigadores avanzan en la cadena de eventos y dan cuenta de interacciones virtuales cada vez más complejas.
Los físicos tienen algoritmos para calcular las probabilidades de escenarios sin bucles o con un bucle, pero las colisiones con dos bucles ya ponen de rodillas a las computadoras. Este es el límite para la precisión predictiva y para que los físicos comprendan las implicaciones de la teoría cuántica.
Sin embargo, todo esto tiene un lado positivo: los físicos no necesitan calcular absolutamente todas las integrales de un diagrama de Feynman complejo, ya que la mayoría de ellas se pueden reunir en uno.
Se pueden reducir miles de integrales a varias docenas de integrales "básicas", que se pueden ponderar y agregar. Pero qué integrales se pueden recopilar en otras básicas separadas es una cuestión computacional difícil. Los investigadores usan computadoras que esencialmente hacen conjeturas basadas en millones de interacciones y tienen dificultades para derivar combinaciones significativas de integrales.
Sin embargo, gracias a los números de intersección, los físicos pueden haber encontrado una manera de seleccionar elegantemente información importante a partir de cálculos extensos de integrales de Feynman.
Huella geométrica
El trabajo de Mastrolia y Mizera surge de una rama de las matemáticas como la topología algebraica , que clasifica formas y espacios. Ayuda en estas teorías de " cohomología ", lo que te permite calcular "huellas dactilares" algebraicas de espacios geométricos complejos.
"Es como una sinopsis, un dispositivo algebraico que captura la esencia del espacio que estás explorando", dijo Clement Dupont, matemático de la Universidad de Montpellier en Francia.
Los diagramas de Feynman se pueden traducir a espacios geométricos, que luego se pueden analizar mediante cohomología. Cada punto de ese espacio puede representar uno de los muchos escenarios que se desarrollan cuando las partículas chocan.
Podríamos esperar que tomando la cohomología de este espacio - encontrando su estructura algebraica - puedas calcular los pesos de las integrales fundamentales. Sin embargo, el espacio geométrico que caracteriza a la mayoría de los diagramas de Feynman es tan curvo que resiste muchos cálculos cohomológicos.
En 2017, Mizera estaba tratando de analizar las colisiones de objetos en la teoría de cuerdas cuando se topó con herramientas inventadas por primera vez por Israel Gelfand y Katsuhiko Aomoto en las décadas de 1970 y 1980 cuando trabajaban en una cohomología llamada cohomología retorcida. Más tarde ese mismo año, Mizera conoció a Mastrolia, quien se dio cuenta de que estas técnicas también podían funcionar en el diagrama de Feynman. El año pasado, publicaron tres artículos que utilizaban la teoría de la cohomología para acelerar los cálculos de colisiones de partículas simples.
Su método toma una familia de escenarios físicos interconectados, lo presenta como un espacio geométrico y calcula su cohomología retorcida. “Y esta cohomología retorcida nos dice todo sobre las integrales que nos interesan”, dijo Mizera.
En particular, la cohomología retorcida indica cuántas integrales básicas se requieren y cuáles deberían ser sus pesos. Estos pesos aparecen como valores que llaman "números de intersección". Como resultado, miles de integrales se secan hasta una suma ponderada de varias docenas de integrales básicas.
Es posible que las teorías de cohomología que producen estos números de intersección puedan hacer más que solo facilitar el cálculo: pueden señalarnos la importancia física de las cantidades más importantes en el cálculo.
Por ejemplo, cuando un gluón virtual se descompone en dos quarks virtuales, su vida útil puede ser diferente. En el espacio geométrico asociado con ellos, cada punto puede denotar una vida útil diferente del quark. Al calcular los pesos, los investigadores ven que los escenarios con las partículas virtuales de mayor duración, es decir, aquellos casos en los que las partículas se vuelven casi reales, influyen en el resultado más que otros.
“Eso es lo sorprendente de este método”, dijo Karon-Hewot. "Él recrea todo, desde estos raros eventos especiales".
La semana pasada Mizera, Mastrolia y sus colegas publicaron otro preprint, donde se demuestra que esta técnica ha evolucionado lo suficiente como para trabajar con diagramas reales con dos bucles. En el próximo trabajo, Karon-Hewot desarrollará este método aún más, posiblemente domesticando incluso los diagramas de tres bucles.
Si tiene éxito, esta técnica podría ayudar a abrir una nueva generación de predicciones teóricas. Y, como sospechan algunos investigadores, incluso puede mostrarnos una nueva perspectiva de la realidad.