Clever Geek Handbook

Experiencia en la optimización de cálculos mediante la generación dinámica de códigos de bytes de JVM.

En mi pequeño proyecto de modelado de variables aleatorias me enfrenté al problema del bajo rendimiento en el cálculo de expresiones matemáticas ingresadas por el usuario, y durante mucho tiempo estuve buscando diferentes formas de resolverlo: intenté escribir un intérprete en C ++ con la esperanza de que fuera rápido, escribí mi propio bytecode. La idea más exitosa resultó ser generar clases JVM y cargarlas en tiempo de ejecución.



Después de aprender sobre KMath , decidí generalizar esta optimización a una variedad de estructuras matemáticas y operadores definidos en ellos.



KMath es una biblioteca de matemáticas y álgebra informática que hace un uso extensivo de la programación orientada al contexto en Kotlin. KMath separa las entidades matemáticas (números, vectores, matrices) y las operaciones sobre ellas; se proporcionan como un objeto separado, un álgebra correspondiente al tipo de operandos, Álgebra <T> . 



import scientifik.kmath.operations.*

ComplexField {
   (i pow 2) + Complex(1.0, 3.0)
}


Por lo tanto, después de escribir un generador de código de bytes, teniendo en cuenta las optimizaciones de JVM, puede obtener cálculos rápidos para cualquier objeto matemático; es suficiente definir operaciones sobre ellos en Kotlin.



API



Para empezar, era necesario desarrollar una API de expresiones y solo entonces pasar a la gramática del lenguaje y al árbol sintáctico. También se le ocurrió la inteligente idea de definir el álgebra sobre las expresiones mismas para presentar una interfaz más intuitiva.



La base de toda la API de expresión es la interfaz Expression <T> y la forma más sencilla de implementarla es definir directamente el método de invocación a partir de los parámetros dados o, por ejemplo, expresiones anidadas. Se integró una implementación similar en el módulo raíz como referencia, aunque la más lenta. 



interface Expression<T> {
   operator fun invoke(arguments: Map<String, T>): T
}


Las implementaciones más avanzadas ya están basadas en MST. Éstos incluyen:



  • Intérprete MST,
  • Generador de clases MST.


Una API para analizar expresiones de una cadena a MST ya está disponible en la rama de desarrollo de KMath, al igual que el generador de código JVM más o menos final.



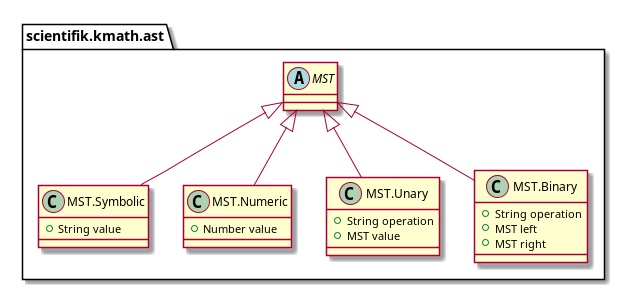
Pasemos a MST. Actualmente hay cuatro tipos de nodos en MST:



  • terminal:

    • símbolos (es decir, variables)
    • números;
  • operaciones unarias;
  • operaciones binarias.






Lo primero que puede hacer con él es omitir y calcular el resultado a partir de los datos disponibles. Al pasar en el álgebra de destino el ID de la operación, por ejemplo "+", y los argumentos, por ejemplo 1.0 y 1.0 , podemos esperar el resultado si se define esta operación. De lo contrario, cuando se evalúe, la expresión caerá con una excepción.







Para trabajar con MST, además del lenguaje de expresión, también hay álgebra, por ejemplo, MstField: 



import scientifik.kmath.ast.*
import scientifik.kmath.operations.*
import scientifik.kmath.expressions.*

RealField.mstInField { number(1.0) + number(1.0) }() // 2.0


El resultado del método anterior es una implementación de Expression <T> que, cuando se llama, provoca un recorrido del árbol obtenido al evaluar la función pasada a mstInField .



Generando código



Pero eso no es todo: al atravesar, podemos usar los parámetros del árbol como queramos y no preocuparnos por el orden de las acciones y la aridad de las operaciones. Esto es lo que se utiliza para generar código de bytes.



La generación de código en kmath-ast es un ensamblado parametrizado de la clase JVM. La entrada es MST y álgebra de destino, la salida es la instancia de Expression <T> .



La clase correspondiente, AsmBuilder , y algunas otras extensiones proporcionan métodos para la construcción imperativa de bytecode sobre ObjectWeb ASM. Hacen que el ensamblaje de clases y el recorrido de MST se vean limpios y requieran menos de 40 líneas de código.



Considere la clase generada para la expresión "2 * x" , se muestra el código fuente de Java descompilado a partir del código de bytes: 



package scientifik.kmath.asm.generated;

import java.util.Map;
import scientifik.kmath.asm.internal.MapIntrinsics;
import scientifik.kmath.expressions.Expression;
import scientifik.kmath.operations.RealField;

public final class AsmCompiledExpression_1073786867_0 implements Expression<Double> {
   private final RealField algebra;

   public final Double invoke(Map<String, ? extends Double> arguments) {
       return (Double)this.algebra.add(((Double)MapIntrinsics.getOrFail(arguments, "x")).doubleValue(), 2.0D);
   }

   public AsmCompiledExpression_1073786867_0(RealField algebra) {
       this.algebra = algebra;
   }
}


Primero, el método de invocación se generó aquí , en el que los operandos se organizaron secuencialmente (ya que están más profundos en el árbol), luego la llamada de adición . Después de la invocación , se registró el método puente correspondiente. A continuación, se escribieron el campo y el constructor de álgebra . En algunos casos, cuando las constantes no se pueden poner simplemente en el grupo de constantes de clase, también se escribe el campo de constantes , la matriz java.lang.Object .



Sin embargo, debido a los muchos casos extremos y optimizaciones, la implementación del generador es bastante complicada.



Optimización de llamadas al álgebra



Para llamar una operación de álgebra, debe pasar su ID y argumentos: 



RealField { binaryOperation("+", 1.0, 1.0) } // 2.0


Sin embargo, tal llamada es costosa en términos de rendimiento: para elegir qué método llamar, RealField ejecutará una declaración de conmutador de tabla relativamente costosa , y también debe recordar sobre el boxeo. Por tanto, aunque todas las operaciones de MST se pueden representar de esta forma, es mejor realizar una llamada directa: 



RealField { add(1.0, 1.0) } // 2.0


No existe una convención especial sobre la asignación de ID de operaciones a métodos en las implementaciones de Algebra <T> , por lo que tuvimos que insertar una muleta, en la que se escribe manualmente que "+" , por ejemplo, corresponde al método add. También hay soporte para situaciones favorables cuando puede encontrar un método para un ID de operación con el mismo nombre, el número requerido de argumentos y sus tipos. 



private val methodNameAdapters: Map<Pair<String, Int>, String> by lazy {
    hashMapOf(
        "+" to 2 to "add",
        "*" to 2 to "multiply",
        "/" to 2 to "divide",
...


private fun <T> AsmBuilder<T>.findSpecific(context: Algebra<T>, name: String, parameterTypes: Array<MstType>): Method? =
    context.javaClass.methods.find { method ->
...
        nameValid && arityValid && notBridgeInPrimitive && paramsValid
    }


Otro gran problema es el boxeo. Si nos fijamos en las firmas de métodos Java que se obtienen tras compilar el mismo RealField, veremos dos métodos: 



public Double add(double a, double b)

// $FF: synthetic method
// $FF: bridge method
public Object add(Object var1, Object var2)


Por supuesto, es más fácil no molestarse con boxear y unboxing y llamar al método bridge: apareció aquí debido al borrado de tipo, para implementar correctamente el método add (T, T): T , cuyo tipo T en el descriptor se borró en java.lang .Objeto .



Llamar a add directamente desde dos dobles tampoco es ideal, porque el valor de retorno es bauxita (hay una discusión sobre esto en YouTrack Kotlin ( KT-29460 ), pero es mejor llamarlo para guardar dos moldes de objetos de entrada en java.lang en el mejor de los casos .Número y su unboxing al doble .



Fue el que más tiempo tardó en resolver este problema. La dificultad aquí no está en crear llamadas al método primitivo, sino en el hecho de que necesita combinar en la pila tanto tipos primitivos (como doble) y sus envoltorios ( java.lang.Double , por ejemplo), e insertar boxing en los lugares correctos (por ejemplo, java.lang.Double.valueOf ) y unboxing ( doubleValue ): no había absolutamente ninguna necesidad de trabajar con tipos de instrucciones en bytecode.



Tenía ideas para colgar mi abstracción mecanografiada encima del código de bytes. Para hacer esto, tuve que profundizar en la API de ObjectWeb ASM. Terminé recurriendo al backend de Kotlin / JVM, examiné la clase StackValue en detalle(un fragmento escrito de código de bytes, que en última instancia conduce a la recepción de algún valor en la pila de operandos), descubrió la utilidad Type , que le permite operar convenientemente con los tipos disponibles en el código de bytes (primitivas, objetos, matrices) y reescribir el generador con su uso. El problema de si encajar o desempaquetar el valor en la pila se resolvió por sí mismo agregando un ArrayDeque que contenía los tipos esperados por la siguiente llamada. 



  internal fun loadNumeric(value: Number) {
        if (expectationStack.peek() == NUMBER_TYPE) {
            loadNumberConstant(value, true)
            expectationStack.pop()
            typeStack.push(NUMBER_TYPE)
        } else ...?.number(value)?.let { loadTConstant(it) }
            ?: error(...)
    }


conclusiones



Al final, pude hacer un generador de código usando ObjectWeb ASM para evaluar expresiones MST en KMath. La ganancia de rendimiento sobre un recorrido MST simple depende del número de nodos, ya que el código de bytes es lineal y no pierde tiempo en la selección y recursión de nodos. Por ejemplo, para una expresión con 10 nodos, la diferencia de tiempo entre la evaluación con la clase generada y el intérprete es del 19 al 30%.



Después de examinar los problemas que encontré, saqué las siguientes conclusiones:



  • necesita estudiar de inmediato las capacidades y utilidades de ASM: simplifican enormemente el desarrollo y hacen que el código sea legible ( Type , InstructionAdapter , GeneratorAdapter );
  • MaxStack , , — ClassWriter COMPUTE_MAXS COMPUTE_FRAMES;
  • ;
  • , , , ;
  • , — , , ByteBuddy cglib.


Gracias por leer.



Autores del artículo:



Yaroslav Sergeevich Postovalov , MBOU “Lyceum № 130 nombrado después El académico Lavrentyev”, un miembro del laboratorio de modelación matemática bajo la dirección de Anton Voytishek Vatslavovich



Tatiana Abramova , investigador del laboratorio de métodos de experimentos de física nuclear en JetBrains Investigación .


More articles:


All Articles