La geometría simpléctica es un campo de estudio relativamente nuevo que influye en gran parte de las matemáticas modernas. Y eso es lo que es.

A principios del siglo XIX, William Rowan Hamilton descubrió un nuevo espacio geométrico con propiedades casi mágicas. Codificó el movimiento y las matemáticas en un solo objeto geométrico hermoso.
Un campo de conocimiento llamado geometría simpléctica surgió de este fenómeno . En las últimas décadas, ha pasado de unas pocas colecciones de ideas a un campo dinámico de investigación con profundas conexiones con más temas de matemáticas y física que Hamilton difícilmente podría haber imaginado.
La geometría simpléctica, de hecho, es el estudio de espacios geométricos de estructura simpléctica. Sin embargo, es necesario aclarar qué significa que el espacio tiene una estructura, sin mencionar ninguna estructura en particular.
Los espacios geométricos pueden ser flexibles como una lona o rígidos como una tienda de campaña. “Las lonas son maleables, pero si se toman un montón de palos y se enmarcan, se obtiene una estructura más estable”, dijo Emmy Murphy de la Universidad Northwestern.
Los espacios menos estructurados son solo un montón de puntos conectados (como una lona). La línea recta es un ejemplo de un espacio unidimensional de este tipo. La superficie de una pelota es un ejemplo bidimensional. Al no existir estructura en estos espacios, es fácil deformarlos sin cambiar a un nivel fundamental. Curva una línea recta; inflar, arrugar, girar la pelota: desde el punto de vista de la topología, estudiando espacios no estructurados, no cambiarán.
“Desde el punto de vista de los topólogos, comenzando con la superficie de una bola, puedes estirarla como quieras y hasta que la rompas, ese espacio no cambia para ellos”, dijo Isa Keating de la Universidad de Cambridge. "Les interesan las características generales de la figura".
Naturalmente, cuando los matemáticos hablan de la deformación del espacio, no se refieren a cambiarlo manualmente. Cambian espacios usando funciones: la función incluye las coordenadas de un punto, y salen las coordenadas de un nuevo punto. Tales transformaciones traducen cualquier punto del espacio en uno nuevo. Este es el equivalente matemático de sacudir una lona.
Puede agregar estructura al espacio. Esta estructura refuerza la información contenida en el espacio, al tiempo que limita las posibilidades de deformación.

Espacio no estructurado: la superficie de la pelota es un espacio bidimensional. La ausencia de una estructura brinda amplias oportunidades para su deformación sin cambiar sus propiedades topológicas.

Agregar estructuras: agregando una estructura métrica al espacio, digamos, como las líneas de latitud y longitud en un globo, podemos medir distancias entre puntos. Pero entonces solo habrá un pequeño conjunto de opciones para la deformación de objetos que no violen estas distancias.
Puede, por ejemplo, agregar una estructura métrica a la superficie de una esfera, como las líneas de latitud y longitud de un globo. Tal estructura nos permitirá medir las distancias entre puntos. Pero después de su aplicación, ya no será posible inflar o arrugar la pelota sin romper la estructura original; después de todo, cambiaremos las distancias entre los puntos. Si inflamos el globo, la distancia entre Nueva York y Londres, por ejemplo, aumentará.
Podemos agregar otro tipo de estructura: simpléctica. Nos da la capacidad de medir áreas en el espacio y nos permite cambiar la forma del espacio para que estas áreas no cambien.
Hamilton encontró el primer ejemplo de tal espacio mientras estudiaba sistemas físicos.- por ejemplo, movimientos planetarios. Cuando un planeta se mueve en el espacio, su ubicación está determinada por tres coordenadas que determinan su posición a lo largo de los ejes x, y y z. Los puntos que representan todas las posibles ubicaciones planetarias forman un espacio tridimensional.
Hamilton descubrió que a cada punto de este espacio tridimensional se le pueden asignar tres coordenadas adicionales, que denotan la magnitud del impulso del planeta a lo largo de los tres ejes. Llamémoslos x m , y m y z m . Ahora tenemos seis coordenadas: tres para la ubicación y tres para el impulso. Estas seis coordenadas definen un punto en el nuevo espacio de seis dimensiones.

Tenemos seis coordenadas: tres para la ubicación y tres para el impulso. Estas seis coordenadas definen un punto en el nuevo espacio de seis dimensiones.
Este espacio de seis dimensiones es un ejemplo de un espacio con una estructura simpléctica, ya que tiene la capacidad de medir áreas. Y así es como funciona.
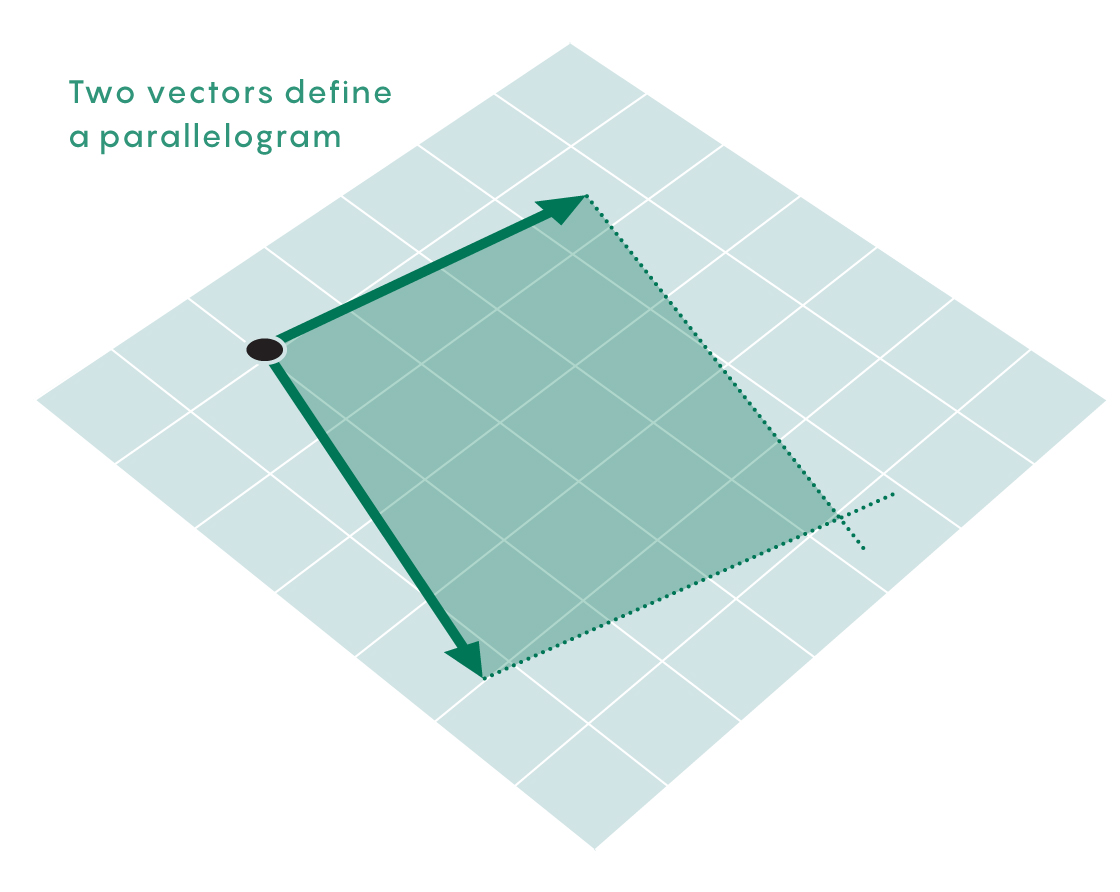
En cada punto del espacio, puede dibujar seis vectores (flechas direccionales) correspondientes a la dirección del movimiento o el momento del planeta a lo largo de la dimensión a la que apunta el vector. Dado que dos vectores forman un paralelogramo, un espacio bidimensional con un área distinta de cero, puede tomar dos vectores y medir esa área.
Para asegurarse de que el valor sea distinto de cero, debe tomar ciertos pares de vectores, que denotan la dirección del movimiento y el momento a lo largo del mismo eje. Los vectores no coincidentes, por ejemplo, el vector direccional del eje z junto con el vector del momento del eje y dan un paralelogramo con área cero.
Estos pares de vectores también reflejan otra propiedad importante del espacio simpléctico: su relación con números complejos. Estos números tienen i, la raíz cuadrada de -1, y tienen la forma a + bi, donde a es real y b es imaginario. Una forma de definir un espacio simpléctico de seis dimensiones es definir tres números complejos, dos partes de cada uno dando una coordenada. Estas dos partes también corresponden a los dos vectores que combinamos para medir el área.
Entonces, para cada punto, por ejemplo, los vectores de dirección de movimiento y momento trazados a lo largo del eje x no solo proporcionan una forma de medir el área, sino que también constituyen uno de los tres números complejos que definen el espacio. Esta relación se refleja en el nombre, porque "simpléctico" proviene de la palabra griega sumplektikós, que significa lo mismo que el complejo latino: "entrelazados". El nombre refleja el entrelazamiento de la estructura simpléctica y los números complejos.
También es una de las principales razones por las que el espacio simpléctico captura la imaginación de los matemáticos. “Los matemáticos ya estaban interesados en números complejos y movimientos planetarios”, dijo Murphy. "Entonces, si le cuenta a un matemático acerca de la existencia de la geometría, lo que muestra por qué estas dos cosas son manifestaciones diferentes de la misma estructura básica, ciertamente estará interesado en este tema".
La geometría simpléctica estudia las transformaciones de espacios que conservan su estructura simpléctica y no cambian el tamaño de las áreas. Esta restricción no da mucho margen para las transformaciones permitidas. Como resultado, la geometría simpléctica ocupa una posición intermedia entre la topología de lona flexible y la geometría rígida de la carpa. Las transformaciones que conservan la estructura simpléctica se denominan, en honor al descubridor, difeomorfismos hamiltonianos .
Sin embargo, Hamilton descubrió solo el primer ejemplo de un espacio simpléctico, y no había razón para insistir en esto. Pronto, los matemáticos empezaron a pensar en cómo se verían los fenómenos simplécticos en espacios geométricos no relacionados con el mundo físico.
"Los matemáticos siempre se esfuerzan por generalizaciones, queremos preguntar: ¿cómo sería la mecánica clásica si viviéramos no en un espacio tridimensional, sino en un espacio de ocho dimensiones?" Murphy dijo.

Vladimir Igorevich Arnold presentó varias hipótesis básicas en el campo de la geometría simpléctica
En la década de 1960, Vladimir Igorevich Arnoldpropuso varias hipótesis influyentes que describen ciertas propiedades del espacio simpléctico que los hacen más rígidos que los topológicos ordinarios. Uno de ellos, la conjetura de Arnold sobre los puntos fijos de los simplectomorfismos, predice que los difeomorfismos hamiltonianos tienen un número inesperadamente grande de puntos “fijos” que no cambian de ubicación durante las transformaciones. Estudiándolos, podemos decir con certeza qué distingue al espacio simpléctico de otros tipos de espacios geométricos.
A finales de la década de 1980, el matemático alemán Andreas Floerdesarrolló la homología de Floer, una poderosa plataforma que los matemáticos usan hoy para estudiar fenómenos simplécticos. Ella usa el llamado. curvas pseudoholomorfas, que indirectamente permiten a los matemáticos contar el número de puntos fijos, determinando un cierto número mínimo de ellos que debe tener un espacio simpléctico.
"La homología de Floer muestra que no se pueden eliminar simplemente puntos fijos", dijo Keating. "Te permite demostrar que estos puntos deben estar ahí".
A medida que se desarrolló la teoría de la geometría simpléctica, se encontraron vínculos con una gama cada vez mayor de temas en matemáticas y física, desde la teoría de cuerdas hasta la topología de baja dimensión y el estudio de una confusa dualidad matemática llamada simetría especular. Un ejemplo reciente de la aplicación de la geometría simpléctica es la solución del problema topológico de las clavijas cuadradas .
Para muchos matemáticos, sin embargo, el atractivo de la geometría simpléctica tiene poco que ver con sus intersecciones con la física u otras áreas de las matemáticas. Consideran que su propia existencia es un milagro. “Comenzamos a encontrar belleza en la estructura misma, independientemente de su relación con cualquier otra cosa”, dijo Murphy.