Relaciones. Parte I

La teoría formal del modelado utiliza relaciones algebraicas, incluyéndolas en las firmas de modelos de estructuras algebraicas, que describen objetos físicos, técnicos e informativos reales, los procesos de su funcionamiento. Entre estos últimos incluyo, por ejemplo, bases de datos (bases de datos relacionales (RDB)). No considero menos importante el campo de la toma de decisiones, que consta de dos principales estadísticos y algebraicos, basados ​​íntegramente en la teoría de las relaciones. El nivel educativo de los especialistas en esta teoría es cercano a cero.



Abra el libro de texto de especialización y allí verá, en el mejor de los casos, sobre equivalencias, que son interpretadas por los autores de una manera muy peculiar. Le pregunto a uno que ya defendió DTN: ¿Considera una relación de equivalencia que no indica ni el portador de la relación, ni una relación específica, cómo se ve en su registro? Respuesta: cómo se ve, normalmente. Resulta que tiene una idea muy vaga de todo esto.



Me resulta difícil nombrar las publicaciones sobre el diseño de un ReDB, a excepción de los artículos extranjeros. En los 90, fue un oponente, escribió una reseña de una tesis, que consideraba bases de datos jerárquicas, en red y relacionales. Pero una vez al año, hace un año y medio, el trabajo volvió a llegar a la revisión, el autor ya escribe solo sobre el DB, sobre la normalización de las relaciones DB, pero no mostró ninguna novedad teórica. Muchas universidades imparten un curso sobre bases de datos, pero no sobre cómo crearlas, crear un DBMS, sino, por regla general, sobre cómo operar una base de datos prefabricada (extranjera).



Rdo. el personal no está preparado para enseñar a los especialistas de TI a crear DBMS, SO, lenguajes de programación domésticos, sin mencionar LSI, VLSI, LSI personalizado. Aquí, aparentemente, el tren partió durante mucho tiempo y durante mucho tiempo. Entonces, en vano, algunas mejillas están hinchadas de orgullo (léase esnobismo), esto se puede ver en los comentarios en las publicaciones de otras personas, demuéstrese que puede, y no se entregue a traducciones inútiles y a volver a cantar las de otra persona por el orgullo: "calificación" y "karma". Afecta no solo la falta de creatividad, sino la simple educación y crianza.



El segundo dominio que está indisolublemente ligado a las relaciones es la toma de decisiones. Cada uno de nosotros está constantemente ocupado con esto. No levantaremos un dedo sin una decisión del consciente o inconsciente. Pocos entienden y menos escriben sobre soluciones. La decisión de cualquier tomador de decisiones (tomador de decisiones) se basa en la preferencia por alternativas. Y el modelo de preferencia es precisamente este tipo de relación, que se denomina "espacio de relaciones de preferencia". Pero quién los estudia. Cuando llegué a un “especialista” en relaciones con una pregunta sobre el número de relaciones de cada tipo, él, sin saber la respuesta, “mató” con una contrapregunta, ¿por qué la necesitas?

Concepto de relación

Creo que el término actitud es familiar para todos los lectores, pero pedir una definición confundirá a la mayoría. Hay muchas razones para esto. Son más a menudo en profesores que, si utilizaron relaciones en el proceso de enseñanza, no se centraron en este término, aparentemente no citaron ejemplos memorables.



En mi memoria hay varios ejemplos memorables para toda la vida. Sobre mapeos y relaciones. Hablaré primero de mapeos. Hay dos cubos de pintura. En uno blanco, en el otro, negro. Y hay una caja de cubos (muchos). Las caras tienen números en relieve. ¿De cuántas formas puedes colorear las caras de los cubos en dos colores? La respuesta es inesperada: tantos como números binarios de 6 bits o 2 ⁶= 64. Permítanme explicar con más detalle f: 2 → 6 2 objetos se muestran en 6. Cada línea de la tabla es una visualización discreta de fi.



Construyamos una tabla con 6 columnas y los colores coincidirán con el número blanco - cero, negro - uno, y las caras del cubo son columnas. Comenzamos con el hecho de que las 6 caras son blancas: este es un vector cero de 6 dimensiones. La segunda línea es una cara negra, es decir, el bit menos significativo se rellena con 1. y así sucesivamente hasta que se agotan los números binarios de 6 bits. Colocamos los cubos en una fila larga común. Cada uno de ellos parece tener un número del 0 al 63.



Ahora la pantalla está invertida. Un paquete de hojas de papel (muchas) y 6 pinturas (rotuladores).

Marque ambos lados de las hojas de papel con rotuladores de diferentes colores. Cuántas hojas se requieren. Respuesta f: 6 → 2 o 6 ² = 36. Estos son mapeos arbitrarios.



Pasemos a las relaciones. Comencemos con un conjunto abstracto: el portador de la relación

A = {a1, a2, a3, ..., an}.

Puedes leer sobre esto aquí . Para una mejor comprensión, reduciremos el conjunto a 3 elementos, es decir A = {a1, a2, a3}. Ahora realizamos la multiplicación cartesiana × = ² ,

× = {(a1, a1), (a1, a2), (a1, a3), (a2, a1), (a2, a2), (a2, a3 ), (a3, a1), (a3, a2), (a3, a3)}.



Obtuvimos 9 pares ordenados de elementos de A × A, en un par el primer elemento del primer factor, el segundo del segundo. Ahora intentemos obtener todos los subconjuntos del cuadrado cartesiano A × A. Primero, un simple ejemplo.



Ejemplo 1... Se da un conjunto A = {a, b, c, d} de 4 elementos. Escriba todos sus subconjuntos. B (A) = {Ø}; {a}; {b}; {c}; {d}; {ab}; {ac}; {ad}; {bc}; {bd}; {cd}; { abc}; {abd}; {acd}; {bcd}; {abcd}; 2 ⁴ = 16 subconjuntos. Este es el booleano B (A) del conjunto A e incluye un subconjunto vacío.



Los subconjuntos contendrán desde A × A un número diferente de elementos (pares): uno, dos, tres, y así sucesivamente hasta los 9 pares, también incluimos el conjunto vacío (Ø) en esta lista. ¿Cuántos subconjuntos hay? Muchos, a saber, 2 ⁹ = 512 elementos.



Definición . Cualquier subconjunto del producto cartesiano (tenemos un cuadrado) de un conjunto se llama relación . Tenga en cuenta que la obra utiliza el mismo conjunto. Si los conjuntos son diferentes, no hay una relación, sino una correspondencia....



Si es un producto cartesiano de dos factores, entonces la relación es binaria , si de 3 es interna, de 4 es tetrar y de n es n-aria. Arity es el número de lugares en una relación. Las relaciones reciben los nombres de las letras mayúsculas R, H, P, S ... Detengámonos en las relaciones binarias (BO), ya que juegan un papel muy importante en la teoría de las relaciones. En realidad, todos los demás pueden reducirse a relaciones binarias.



El símbolo de relación se coloca a la izquierda de los elementos R (x, y) o entre ellos x R y; x, y є A.

Definición El conjunto de todos los subconjuntos del conjunto A se llama booleano. Nuestro booleano consta de 2 ^{| A × A |} elementos, aquí | A × A | Es la cardinalidad del conjunto.



Las relaciones se pueden establecer en diferentes representaciones sobre A = {a1, a2, a3, a4}:

• enumeración de elementos; R1 = {(a1, a2), (a1, a3), (a2, a3) (a2, a4) (a3, a2) (a3, a4}
• binario n = vector de 16 bits; <0110001101010000>;
• matriz;

Figura 1.2. a) Matriz 4 × 4 de relación binaria b) Numeración de celdas de la matriz



Aquí, se utilizan números de celda, rellenados con los de la Fig. 1b)

- Representación vectorial. Un vector binario para representar una relación binaria se forma a partir de los elementos {0,1} de la siguiente manera:



El ejemplo considerado de establecer una relación en forma vectorial se verá así:





- Representación gráfica. Asociamos los elementos del conjunto

A = {x1, x2, z3, ..., xn} con puntos en el plano, es decir, los vértices del gráfico G = [Q, R].



Dibuje un arco en la gráfica de (xi) a (xj) si y solo si el par (xi, xj) є R (para i = j, el arco (xi, xi) se convierte en un bucle en el vértice (xi). Ejemplo (Fig. 1a) La representación de una relación binaria A [4 × 4] mediante un gráfico se muestra en la figura 2.2.



Figura 2.2. Representación de una relación mediante un gráfico dirigido



Catálogo de relaciones binarias (n = 3)



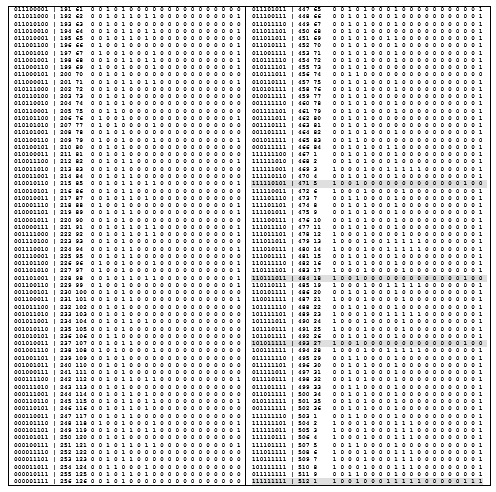
Grande se ve a distancia. Para tener una idea de su diversidad, tuve que crear manualmente un catálogo de relaciones binarias sobre un conjunto de 3 elementos, que incluía todas las relaciones (más de 500 relaciones). Después de eso, vino o se fue la relación.



Obviamente, el catálogo incluirá 2 ^{3 × 3} = 2 ⁹relaciones, y cada uno de ellos estará equipado con un conjunto de propiedades inherentes. A continuación (Tabla 3) hay una lista completa de las 512 relaciones sobre el conjunto A, | A | = 3, de tres elementos. También se dan los resultados del cálculo del número de razones (Tabla 2), representados por combinaciones de los números de celdas del cuadrado cartesiano 3 × 3, de diferentes subclases para diferentes valores de la cardinalidad del conjunto de portadores (n = 3). Para cada relación se indican sus propiedades básicas y la pertenencia al tipo (Tabla 3). Las abreviaturas utilizadas en el catálogo se describen en la Tabla 2

Tabla 2. Características cuantitativas del catálogo para diferentes n





Es conveniente explicar la esencia de las operaciones con relaciones y su técnica utilizando ejemplos especialmente sencillos y comprensibles para las relaciones binarias. Las operaciones pueden involucrar dos y / o más relaciones. Las operaciones realizadas sobre relaciones individuales son operaciones unarias. Por ejemplo, operaciones de invertir (recibir inversas) relaciones, tomar complemento, estrechar (limitar) una relación. Un ejemplo ilustrará cómo utilizar el catálogo.



Ejemplo 2 . Considere la línea Npr = 14 de la tabla de catálogo. Tiene la forma



Los primeros 9 caracteres de la línea (a la derecha de la igualdad) es un vector binario correspondiente a una combinación de 9 a 2, es decir, el número de la primera celda (contando de izquierda a derecha) es el número de la quinta celda de la matriz de la relación binaria, es decir, elementos a1a1 = a2a2 = 1. Esta combinación tiene un número de serie Ncc = 4 y un número intermedio Npr = 14 en la lista de todas las relaciones. El resto de esta línea contiene ceros o unos. Los ceros indican la ausencia de una propiedad correspondiente al nombre de la columna cero y los unos indican la presencia de dicha propiedad en la relación considerada.

Propiedades y características cuantitativas de las relaciones.

Consideremos las propiedades más importantes de las relaciones, lo que nos permitirá resaltar aún más los tipos (clases) de relaciones que se utilizan en las bases de datos relacionales en la teoría de la elección y la toma de decisiones y otras aplicaciones. En lo que sigue, denotaremos la relación con el símbolo [R, Ω]. R es el nombre de la relación, Ω es el conjunto de portadores de la relación.



1. Reflexividad. La relación [R, Ω] se llama reflexiva si cada elemento del conjunto está en la relación R consigo mismo (figura 2.3). La gráfica de un BO reflexivo tiene bucles (arcos) en todos los vértices, y la matriz de relación contiene (E) la diagonal principal unitaria.





Figura 2.3. Actitud reflexiva



2. Antirreflectante. La relación [R, Ω] se llama antirreflexivo si ningún elemento del conjunto está en la relación R consigo mismo (figura 2.4). Las relaciones antirreflectantes se llaman estrictas.





Figura 2.4. Actitud



anti-reflexiva 3. Reflexividad parcial. La relación [R, Ω] se llama parcialmente

reflexiva si uno o más elementos del conjunto no están en la relación R consigo mismo (figura 2.5).





4. Simetría. Una relación [R, Ω] se llama simétrica si, junto con un par ordenado (x, y), la relación también contiene un par ordenado (y, x) (figura 2.6).





5. Antisimetría. Una relación [R, Ω] se llama antisimétrica si, si, para cualquier par ordenado (x, y) є R, un par ordenado

(y, x) єR, solo en el caso x = y. Para tales relaciones R∩R ^-1 ⊆ E (Fig. 2.7).





6. Asimetría. Una relación [R, Ω] se llama asimétrica si es antirreflexiva y para cualquier par ordenado (x, y) є R un par ordenado (y, x) ∉ R, para las relaciones R ∩ R ^-1 = Ø (Fig. 2.8).





7. Transitividad. La relación [R, Ω] se llama transitiva si, para cualquier par ordenado (x, y), (y, z) є R, en la relación R hay un par ordenado (x, z) є R o si R × R⊆R (Fig. . 2.9).





8. Ciclicidad. Una relación [R, Ω] se llama cíclica si para sus elementos {x1, x2, z3, ..., xn} hay un subconjunto de elementos {xi, xi + 1, ... xr, ..., xj, xi}, para lo cual podemos escribir la secuencia xiRxi + 1R ... RxjRxi. Esta secuencia se denomina ciclo o bucle (figura 2.10).





9. Aciclicidad. Las relaciones en las que no hay contornos se denominan acíclicas. Para relaciones acíclicas, la relación R ^k ∩R = Ø se satisface para cualquier k> 1 (figura 2.11).







10. Integridad (conectividad). La relación [R, Ω] se llama completa (conectada) si para dos elementos cualesquiera (y, z) є Ω uno de ellos está en relación con el otro (figura 2.12). Linealidad. Las relaciones lineales son relaciones mínimamente completas.





Figura 2.12. Relación lineal



Entonces, hemos establecido que las relaciones, como objetos matemáticos, tienen ciertas propiedades, cuya definición se dio anteriormente. En el siguiente párrafo, consideraremos la esencia y manifestación de algunas propiedades:

1. Reflexividad x є A (xRx).
2. Antirreflexividad x є A ¬ (xRx).
3. Simetría x, y є A (xRy → yRx).
4. Antisimetría (xRy & yRx → x = y).
5. Transitividad; x, y, z є A (xRy & yRz → xRz).
6. Ciclicidad; x, y є A; ...
7. Completitud x, y є (xRy, yRx);
8. Conectividad (x ≠ y → xRy, yRx).
9. Linealidad x, y є (xRy, yRx).

El análisis del espacio de relaciones es una tarea compleja de la teoría y, cabe señalar, dista mucho de ser completa. Los principales resultados deben incluir la selección de subconjuntos de relaciones que forman espacios completos de relaciones con todas las consecuencias consiguientes.



Las relaciones cuantitativas de estos espacios discretos son de gran interés tanto

teórico como práctico. Algunos aspectos de las características cuantitativas asociadas con las propiedades de las relaciones de diferentes tipos se consideran a continuación.

Operaciones sobre relaciones

Como la mayoría de los sistemas numéricos con relaciones, se realizan las siguientes operaciones:

• unario
• binario;
• n-ary.

A continuación se muestran tablas de suma y multiplicación booleana ⊕ y de dos variables x1 y x2, suma mod 2 y suma binaria:





Arriba, se introdujo el concepto de relación binaria, como un subconjunto de pares ordenados del producto cartesiano de conjuntos, y también se consideraron las propiedades de las relaciones. Además, se mencionaron las relaciones binarias y la representación matricial de relaciones. Consideremos ahora el concepto de relación con más detalle, además, consideremos las operaciones básicas de las relaciones binarias, las más importantes de su conjunto de relaciones.



Para ellos, se deben cumplir las siguientes condiciones:

• La aridad de los operandos en la operación debe coincidir;
• el resultado de la operación debe ser una relación de la misma aridad.

Para las relaciones binarias y n-arias, se debe cumplir lo siguiente: el área de llegada del primer operando debe coincidir con el área de origen del segundo operando.



Operaciones unarias sobre relaciones



Inversión de relaciones . La inversa de la relación R es la relación R ^-1 definida por la condición xR ^-1 y <=> yRx. Más correctamente, esta operación debería llamarse pseudo-inversión, ya que p · p ^-1 ≠ E = Δ.



Sea la relación P escrita en forma de enumeración de los pares ordenados incluidos en ella. Si en cada par se intercambian los componentes, entonces los nuevos pares forman la relación P ^-1 , que se denomina inversa a P.



La relación inversa a la relación P es la relación que está formada por pares (ai aj) para los cuales (aj ai) є P ^-1 . Para relaciones en forma matricial, las relaciones inversas se obtienen por transposición de la matriz P.



9. La relación dual (P ^d ) con la relación P es la relación formada por todos aquellos pares que pertenecen a la relación universal y no pertenecen a la relación inversa (suma a la inversa):



P ^d = {(ai aj) | ((ai aj) єA × A) & (ai aj) ∉ P ^-1 )} = (A × A) \ P ^-1 .



Las relaciones duales e inversas en el agregado contienen todos los pares del producto cartesiano A × A y no tienen pares comunes, al igual que las relaciones P y P formar una partición A × A





Tenga en cuenta que para cualquier relación P no se satisface P P = ^d .



Estrechamiento (PA1). La relación [R1, A1] se denomina restricción de la relación [R, A] al conjunto Ω1 si Ω1⊆ Ω y R1 = R∩Ω1 × Ω1. El cociente PA1 del conjunto A1 ⊆ A es el cociente PA1 del conjunto A1, formado por todos aquellos pares que pertenecen a la relación P y son simultáneamente parte del producto cartesiano A1 × A1. En otras palabras, PA1 es la intersección de las relaciones P y A1 × A1. Sea A1 = {a1, a3, a4}, entonces para las relaciones P y Q en forma matricial, las relaciones de estrechamiento tendrán la forma:





Operaciones binarias Las



operaciones que requieren al menos dos relaciones son n-arias (n-arias). Sólo las relaciones de la misma aridad pueden participar en tales operaciones. Ejemplos de tales operaciones: intersección, unión, diferencia, diferencia simétrica de relaciones y algunas otras. Si la operación usa más de dos relaciones, entonces se realiza secuencialmente para las dos primeras, y luego para la relación final y la tercera, etc.



En otras palabras, estas operaciones se definen para dos relaciones. En operaciones sobre relaciones, se asume que los dominios para especificar relaciones (operandos y resultado) coinciden, las aridades de las relaciones coinciden y el resultado de la operación es nuevamente una relación de la misma aridad. Como ejemplos, consideraremos operaciones sobre relaciones binarias P y Q definidas en un conjunto discreto

= {a1, a2, a3, a4} por matrices booleanas (como regla, los ceros no caben en la matriz):





1. La intersección (P ∩ Q) es una relación formada por todos aquellos pares de elementos de A que están incluidos en ambas relaciones, es decir común a P y Q,

P ∩ Q = {(ai aj) | ((ai aj) є P) y ((ai aj) є Q)}.



La matriz de razón P ∩ Q se obtiene como la intersección booleana de las matrices P y Q:





En ausencia de tales pares comunes, se dice que la intersección de relaciones está vacía, es decir es una relación nula. La intersección de las relaciones R1 y R2 (R1∩R2) es la relación determinada por la intersección de los subconjuntos correspondientes de A × A.



2. Unión (PUQ). La unión de las relaciones R1 y R2 (R1UR2) es la relación definida por la unión de los subconjuntos correspondientes de A × A. La razón formada por todos los pares que componen la razón P o la razón Q, es decir por pares pertenecientes a al menos una de las relaciones (la conectiva ∨ - o la unificadora)

PUQ = {(ai aj) | ((ai aj) є P) ∨ ((ai aj) є Q)}.



Si en el conjunto A × A no hay otros pares que no estén incluidos en la relación PUQ, y su intersección es cero, entonces se dice que las relaciones P y Q forman una relación A × A completa cuando se combinan, y su sistema es una partición de esta relación completa. La unión de las matrices de relación se forma como una suma booleana de las matrices de relación:





3. La diferencia (P \ Q) es la razón formada por los pares de P que no están incluidos en la relación Q

P \ Q = {(ai aj) | ((ai aj) є P) y ((ai aj) ∉Q)}.



La diferencia para las relaciones en la representación matricial es





4. Multiplicar relaciones. Los pares ordenados que forman una relación pueden contener o no los mismos elementos. Entre los pares que tienen elementos idénticos en su composición, destaquemos los pares ordenados, que llamamos adyacentes (contiguos) y que tienen el primer elemento en el segundo par, y el segundo elemento en el primer par es el mismo. Definamos el producto de pares adyacentes como un par ordenado:

(ai ak) ∙ (ak aj) => (ai aj).



En términos de teoría de grafos, lo anterior significa que los pares adyacentes forman una ruta desde el punto (ai) al punto (aj) en tránsito a través del punto (ak), que consta de 2 arcos adyacentes. El producto de estos arcos es el tercer arco del punto (ai) al punto (aj), que implementa la transición entre los puntos extremos del recorrido en la misma dirección, sin pasar por el punto intermedio (ak). Se dice que el arco (ai aj) cierra estos puntos directamente.



5. Diferencia simétrica (P∆Q): la relación formada por los pares que están incluidos en la unión PUQ, pero no están incluidos en la intersección P∩Q. Otra forma de definición explica el nombre de la operación: P∆Q está formado por esos pares ordenados que son la unión de las diferencias P \ Q y Q \ P. Por lo tanto, la expresión de la diferencia simétrica se puede escribir de dos formas diferentes:

P∆ Q = (PU Q) \ (P ∩ Q) = (P \ Q) U (Q \ P).



La matriz de diferencias simétricas es:





Del último registro se deduce que la operación de diferencia simétrica permite la permutación de los operandos, es decir, es conmutativa.



5. La composición o producto (P ∙ Q) es una relación formada por todos los pares para los cuales:

P ∙ Q = {(ai aj) | ((ai ak) є P) & ((ak aj) є Q)}.



En otras palabras, cada par ordenado en la relación resultante es el resultado de la multiplicación de pares adyacentes, de los cuales el primer par pertenece a la primera relación factorial, el segundo a la segunda relación factorial. La operación de composición no es conmutativa.



La composición (◦Q) en un conjunto M es una relación R definida en el mismo conjunto M que contiene un par (x, y) cuando existe Z є M tal que (x, z) є P y (z, y) є Q.



En la representación matricial de relaciones, la composición de la matriz de relaciones es igual al producto booleano de las matrices de las relaciones originales:





Un caso especial de la composición de relaciones es el cuadrado de la relación.



Se puede demostrar mediante inducción que el n-ésimo grado de una relación se define recursivamente mediante la fórmula: P ⁿ = P ^n-1 ◦, esto significa que el par (x, y) є P ⁿ en el caso en que la matriz contenga una cadena elementos: tales que (xi, xi + 1) є P, 1 <i <n - 1.



La operación de composición tiene la propiedad de asociatividad (como un producto de matrices).



La composición de relaciones en el conjunto M es el resultado de una composición por pares de relaciones para cualquier arreglo de paréntesis. El área para configurar el resultado de la composición no cambia.



La composición de las matrices de relaciones booleanas se forma como resultado del producto booleano de las matrices de estas relaciones.



Tabla 3. Catálogo de relaciones binarias (n = 3). Clickable