
Otros artículos del ciclo
La teoría formal del modelado utiliza relaciones algebraicas, incluyéndolas en las firmas de modelos de estructuras algebraicas, que describen objetos físicos, técnicos reales y los procesos de su funcionamiento. Esta publicación es una continuación de la anterior , cuya lectura es deseable, ya que allí se describen muchos conceptos y términos aquí empleados.
La presentación no se ofrece en el estilo tradicional (flecha), sino en la forma en que yo mismo tuve que representar y dominar toda esta cocina, tanto de libros de texto / manuales como de artículos de revistas. Considero que el catálogo que he creado es especialmente útil, te permite seleccionar casi cualquier espacio y presentar sus elementos en una forma conveniente: una matriz, un gráfico, etc.Puedes ver inmediatamente de qué estás tratando y las propiedades (ya están escritas) a menudo no necesitan ser revisadas.
Concepto de relación
Creo que el término actitud es familiar para todos los lectores, pero pedir una definición confundirá a la mayoría. Hay muchas razones para esto. Con mayor frecuencia se encuentran en maestros que, si utilizaron relaciones en el proceso de enseñanza, no se centraron en este término, no dieron ejemplos memorables. Algunos comentaristas del artículo atribuyeron los comentarios a su propia cuenta y agregaron desventajas. Pero no puedes esconder una costura en un saco. No hubo publicaciones serias y no. Pregúntate, ¿has trabajado con algún espacio de relación? Y honestamente respóndete. ¿Qué puedes decirle al mundo sobre este espacio? Para empezar, al menos enumera sus elementos y especifica propiedades. Incluso miras el DBMS a través de los ojos de sus creadores, pero ellos tampoco ven todo, o no muestran todo, como, por ejemplo, en microcircuitos.
Haré una pequeña repetición aquí. Uno debe comenzar con el conjunto abstracto A = {a1, a2, a3, ..., an}. Puedes leer sobre esto aquí . Para una mejor comprensión, reduciremos el conjunto a 3 elementos, es decir = {a1, a2, a3}. Ahora realizamos la multiplicación cartesiana × = 2 y enumeramos explícitamente todos los elementos del cuadrado cartesiano
× = {(a1, a1), (a1, a2), (a1, a3), (a2, a1), (a2, a2 ), (a2, a3), (a3, a1), (a3, a2), (a3, a3)}.
Obtuvimos 9 pares ordenados de elementos de A × A, en un par el primer elemento es del primer factor, el segundo del segundo. Ahora intentemos obtener todos los subconjuntos del cuadrado cartesiano A × A. Los subconjuntos contendrán un número diferente de pares: uno, dos, tres, y así sucesivamente hasta los 9 pares, también incluimos el conjunto vacío ∅ en esta lista. ¿Cuántos subconjuntos hay? Muchos, a saber, 2 9= 512 elementos.
Definición . Un subconjunto de un conjunto de cuadrados cartesianos se llama relación binaria. Si el cuadrado cartesiano de dos factores es una razón binaria, si de 3 es interno, de 4 es tetrar y de n es n-ario. Arity es el número de lugares en un elemento de relación.
Definición . El conjunto de todos los subconjuntos del conjunto A se denomina booleano. Booleano consta de 2 | A | elementos, aquí | A | Es la cardinalidad del conjunto.
Las relaciones se pueden definir de diferentes formas:
- enumeración de elementos; R1 = {(a2, a2), (a2, a3), (a3, a1)}; R2 = {(a3, a3)}
- vector binario; <000011100>; <000000001>
- matriz;
- gráfico y otras formas.
A continuación, pasamos a la consideración de los espacios de relaciones, asumiendo que el concepto, las propiedades de las relaciones y las operaciones con ellos son familiares para el lector al menos en la medida de nuestra publicación en el enlace.
Espacios de relación binaria
Aclaremos de forma preliminar que las relaciones pueden ser estrictas (todas estas son relaciones antirreflectantes) o no estrictas (todas las demás). Nos centraremos en la relación de indiferencia y preferencia, estas últimas se subdividen en preferencias débiles y preferencias estrictas (por alguna razón, no fuertes). En general, no hay orden en la ciencia con la terminología y lo más probable es que no lo haya. En criptografía, por ejemplo, eliminar un cifrado de un criptograma en presencia de una clave es descifrar, y sin clave, descifrar. Parecería que un decodificador decodifica, pero no.
El espacio de relaciones binarias con un conjunto de portadores es un subconjunto arbitrario del conjunto de relaciones binarias dado en. Considere los espacios principales para las relaciones de preferencia (Figura 2.15).
R- el espacio de todas las relaciones de preferencia débil, satisface la condición de reflexividad e integridad.
QT : preferencias débiles que satisfacen la condición de cuasi transitividad.
QO es el espacio de cuasiórdenes lineales, es decir, relaciones de QT que son transitivas.
TO es el espacio de todos los órdenes perfectos, es decir, relaciones de QO que son antisimétricas.
SP : el espacio de todas las relaciones de preferencia estricta, satisface las propiedades de antirreflexividad y antisimetría.
RO- Relaciones de estricto orden parcial o preferencias transitivas estrictas. Dado que las relaciones de orden parcial estricto son transitivas, es natural utilizarlas para representarlas mediante gráficas reducidas, es decir, aquellas en las que se omiten los arcos de transitividad. Estos gráficos abreviados se denominan diagramas de Hasse.
QS es el espacio de cuasiseries, es decir, órdenes parciales estrictos para los que la relación I = ¬ (PUP -1 ) es una equivalencia.
TSO es el espacio de órdenes lineales estrictos, es decir, aquellos órdenes parciales para los que se satisface la propiedad de completitud.
Cabe señalar que hay n de tales relaciones en total. Por ejemplo, para n = 3, el número de relaciones perfectas es 6, y todas se muestran en la Fig. 2.13.
T- el espacio de todas las relaciones de tolerancia (indiferencia), tienen las propiedades de simetría y reflexividad.
TOT es el espacio de relaciones de tolerancia de orientación transitiva, es decir, relaciones tales que el complemento de I se representa como una unión de relaciones transitivas mutuamente inversas, es decir,
¬I = R∩R -1 .
Yo es el espacio de todas las relaciones de equivalencia, es decir, relaciones simétricas, reflexivas y transitivas.
E - espacio de relaciones de igualdad, consiste en una relación representada por una matriz diagonal. Existe una relación uno a uno entre los espacios R, P e I, determinada por el mapeo de las relaciones de preferencia.


Figura 2.15 Esquema de espacios de relaciones binarias
Las conexiones reveladas entre los espacios se utilizan para transferir problemas de toma de decisiones (DM) de un espacio a otro, donde se pueden resolver de forma más sencilla, y luego la solución resultante se devuelve al espacio original, donde se formuló el DP.
Estas relaciones se muestran esquemáticamente en la Fig. 2.14. Los espacios de relaciones binarias (tipos de relaciones) se muestran en la Fig. 2.15.
Relaciones de equivalencia
Definición . Una relación binaria σ ⊆ A × A, que tiene tres propiedades de reflexividad, simetría y transitividad, se llama relación de equivalencia binaria (BOE). Se denota la relación de equivalencia σ (x, y), (x, y) ∊σ, xσy, xy. Es conveniente utilizar una representación matricial (tabular) de la relación. A continuación, en la Figura 2.24, hay solo una representación matricial. Sobre el conjunto de 4 elementos, hay 15 BOE, todos representados.
Representación y análisis de la estructura de relaciones de equivalencia (n = 4)
La equivalencia de relaciones binarias es quizás el BO más común. Rara vez la ciencia se las arregla sin este concepto, pero incluso cuando se utilizan equivalencias para formular preguntas, puede ser difícil entender lo que quiso decir el autor. Incluso con la correcta definición y enumeración de las propiedades inherentes a esta relación binaria, persisten las dificultades de percepción.
Comencemos con un ejemplo de equivalencias, que ilustra las limitaciones de su número.
Ejemplo 1 . Que haya tres cubos. Hagamos una lista de las propiedades de las que están dotados los cubos y el uso práctico de las cuales (las propiedades de los cubos) los hace, por así decirlo, intercambiables. Asignemos números a los cubos y representemos sus propiedades en la Tabla 1.
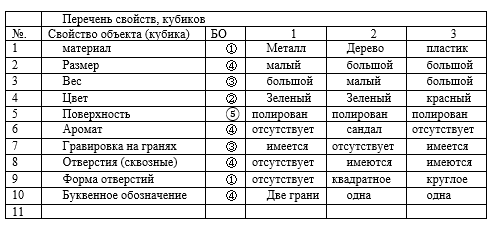
Para cada una de las propiedades, surgen BOE y clases de equivalencia. Continuando con la lista de propiedades, no obtendremos nuevas relaciones de equivalencia. Solo habrá repeticiones de los ya construidos, pero para otros signos. Demostremos la conexión entre BOE y conjuntos.
Considere un conjunto de tres elementos A = {1,2,3} y obtenga todas las particiones posibles en todas las partes. ①1 | 2 | 3; ②12 | 3; ③13 | 2; ④ 1 | 23; ⑤123. La última división en una parte. Números de partición y BO en círculos.
Definición . Una partición de un conjunto A es una familia i, i = 1 (1) I, de subconjuntos disjuntos por pares no vacíos de , cuya unión forma el conjunto original completo = Ui, i∩j = ∅, ∀ i ≠ j. Los subconjuntos i se denominan clases de equivalencia de la partición del conjunto original.
Todas estas son particiones del conjunto (5 piezas). El análisis de BO muestra que también hay solo 5 relaciones de equivalencia diferentes. ¿Es esta coincidencia una coincidencia? Podemos asociar cada partición con una matriz de nueve celdas (3 × 3 = 9), cada una de las cuales contiene un par ordenado de elementos del conjunto A, o la celda permanece vacía si no hay ningún objeto para el par correspondiente. Las filas y columnas de la matriz están marcadas con elementos del conjunto A, y la intersección fila-columna corresponde a un par ordenado (i, j). No es un par que encaja en la celda de la matriz, sino simplemente uno o cero, sin embargo, el cero a menudo no se escribe en absoluto.
No, la coincidencia no es casual. Resulta que cada partición del conjunto está en correspondencia uno a uno con el BOE, y la cardinalidad del conjunto puede ser cualquiera | A | = n.
Esta relación es quizás la más frecuente en términos de uso en la circulación científica, pero el conjunto de propiedades realizadas al respecto limita enormemente su prevalencia.
Entonces, entre todas las relaciones binarias abstractas sobre un conjunto de tres elementos (hay 2 9 = 512 relaciones en total ), solo cinco son equivalencias: portadores de las propiedades requeridas, menos del uno por ciento.
Para | A | = Existen 4 relaciones 2 16= 65536, pero solo hay 15 equivalencias. Este es un tipo de relación muy poco común. Por otro lado, las relaciones de equivalencia están muy extendidas en los problemas aplicados. Dondequiera que haya y se consideren conjuntos de objetos muy diferentes y diferentes particiones de tales conjuntos (no números) en partes, surgen relaciones de equivalencia. Pueden denominarse modelos matemáticos (algebraicos) de tales particiones, que clasifican conjuntos de objetos de acuerdo con varios criterios.
La partición mínima del conjunto A formada por subconjuntos de un elemento A = U {a} y la partición A que consta del conjunto {A} en sí se denominan particiones triviales (impropias).
Celosía P (4): todas las particiones del conjunto A = {a1, a2, a3, a4} = {1,2,3,4}

La partición mínima corresponde a la relación de equivalencia P15, que se denomina igualdad o relación unitaria. Cada clase de equivalencia contiene un solo elemento. A una partición del conjunto A, que incluye solo el propio conjunto A, corresponde una relación de equivalencia que contiene todos los elementos del cuadrado cartesiano A × A.

El tipo más cercano a las relaciones de equivalencia son las relaciones de tolerancia . El conjunto de relaciones de tolerancia contiene todas las relaciones de equivalencia. Para el portador A hay tres elementos de tolerancia 8. Todos ellos tienen las propiedades de reflexividad y simetría.
Cuando se cumple la propiedad de transitividad, cinco de las ocho tolerancias se transforman en equivalencias (Figuras 2.24 y 2.25).
Definición . El conjunto de clases de equivalencia [a] σ de los elementos del conjunto A se denomina conjunto cociente (denotado por A / σ) del conjunto A por la equivalencia σ.
Definición . Un mapeo natural (canónico) f: A → A / σ es un mapeo f tal que f (a) = [a] σ.
Relaciones de tolerancia y su análisis
Estos BO ya se han mencionado anteriormente, pero aquí los consideraremos con más detalle. Todo el mundo conoce los conceptos de similitud, similitud, similitud, indistinguibilidad, intercambiabilidad de objetos. Parecen ser similares en contenido, pero no lo mismo. Cuando solo se indica similitud para objetos, es imposible dividirlos en clases claras de modo que dentro de la clase los objetos sean similares y no haya similitud entre objetos de diferentes clases. En el caso de similitud, surge una situación vaga sin límites claros. Por otro lado, la acumulación de diferencias insignificantes en objetos similares puede dar lugar a objetos completamente diferentes.
En la parte anterior, discutimos el significado significativo de la relación de semejanza (equivalencia) de objetos. Igualmente importante es la situación en la que es necesario establecer la similitud de los objetos.
Estudiemos la forma de los cuerpos geométricos. Si la similitud de la forma de los objetos, por ejemplo, cubos, significa su completa intercambiabilidad en una determinada situación de aprendizaje, entonces la similitud es intercambiabilidad parcial (cuando entre los cubos hay paralelepípedos que son muy similares a ellos), es decir, la posibilidad de intercambiabilidad con algunos (admisible en esta situación ) pérdidas.
La mayor medida de similitud es la indistinguibilidad, en absoluto la similitud, como podría parecer a primera vista. La identidad es una propiedad cualitativamente diferente. La identidad solo puede verse como un caso especial de indistinguibilidad y similitud.
El punto es que los objetos indistinguibles (así como los similares, similares) no se pueden dividir en clases, de modo que los elementos de cada clase no difieran y los elementos de diferentes clases sean obviamente diferentes.
De hecho, consideraremos el conjunto de puntos (x, y) en el plano. Deje que el valor d tenga un valor menor que el umbral de resolubilidad del ojo, es decir, d es una distancia a la que dos puntos ubicados a esta distancia se fusionan en uno, es decir, visualmente indistinguible (a la distancia seleccionada del plano del observador). Considere ahora n puntos que se encuentran en una línea recta y separados (cada uno de los vecinos) a una distancia d. Cada par de
puntos adyacentes es indistinguible, pero si n es lo suficientemente grande, el primero y el último puntos estarán muy separados entre sí y ciertamente serán distinguibles.
El enfoque tradicional para el estudio de la similitud o indistinguibilidad es determinar primero el grado de similitud y luego examinar la posición relativa de objetos similares. El matemático inglés Ziman, al estudiar modelos del aparato visual, propuso una definición axiomática de similitud. Así, fue posible estudiar las propiedades de la similitud independientemente de cómo se especifica exactamente en una situación dada: la distancia entre objetos, la coincidencia de algunos signos o la opinión subjetiva del observador.
Introduzcamos una explicación del concepto de similitud o indistinguibilidad.
Definición . La relación T en el conjunto M se llama relación de tolerancia o tolerancia si es reflexiva y simétrica.
La exactitud de esta definición es evidente por el hecho de que el objeto es obviamente indistinguible de sí mismo y, por supuesto, se parece a sí mismo (esto da la reflexividad de la relación). El orden de consideración de dos objetos no afecta la conclusión final sobre su similitud o disimilitud (simetría).
A partir del ejemplo con indistinguibilidad visual de puntos en el plano, vemos que la transitividad de tolerancia no se cumple para todos los pares de objetos.
También está claro que, dado que la similitud es un caso especial de similitud, la equivalencia debe ser un caso especial de tolerancia. Comparando las definiciones de equivalencia y tolerancia, estamos convencidos de que este es el caso. El principio filosófico: "lo particular es más rico que lo general" está claramente confirmado. Una propiedad adicional: la transitividad hace que algunas de las relaciones de tolerancia sean equivalentes. Dos gemelos son tan parecidos que pueden examinarse el uno al otro sin ningún riesgo. Sin embargo, si dos estudiantes solo son iguales, ese truco, aunque factible, es arriesgado.
Cada elemento del conjunto lleva cierta información sobre elementos similares a él. Pero no toda la información, como en el caso de elementos idénticos. Aquí, son posibles diferentes grados de información que contiene un elemento en relación con otro.
Consideremos ejemplos en los que la tolerancia se establece de diferentes maneras.
Ejemplo 2 . El conjunto M consta de palabras rusas de cuatro letras, sustantivos comunes en el caso nominativo. Llamaremos similares a estas palabras si no difieren en más de una letra. El conocido problema "Convertir una mosca en un elefante" en términos precisos se formula de la siguiente manera. Encuentre una secuencia de palabras que comiencen con la palabra "volar" y terminen con la palabra "elefante", dos palabras adyacentes cualesquiera que sean similares en el sentido de la definición que se acaba de dar. La solución a este problema:
volar - mura - tura - tara - kara - plaza - café - kaffr - musher - esquife - anzuelo - cocodrilo - fecha límite - escorrentía - gemido - elefante.
Ejemplo 3... Sea p un número natural. Denotamos por Sp la colección de todos los subconjuntos no vacíos del conjunto M = {1, 2, ..., p}. La relación "tener al menos un elemento común" en el conjunto Sp es una relación de tolerancia. Entonces, dos de esos subconjuntos se denominan tolerantes si tienen al menos un elemento común. Es fácil ver que se cumple la reflexividad y simetría de la relación.
El conjunto Sp se llama simplex (p –1) -dimensional. Este concepto generaliza el concepto de segmento, triángulo y tetraedro al caso multidimensional. Los números 1, 2, 3, ..., p se interpretan como vértices de un simplex. Subconjuntos de dos elementos - como aristas, tres elementos - como caras planas (bidimensionales), otros subconjuntos de k elementos - como caras (k –1) -dimensionales. El número de todos los elementos (subconjuntos) de Sp es igual a 2 p - 1.
La tolerancia de subconjuntos (caras) significa que tienen vértices comunes.
Definición . El conjunto M con la relación de tolerancia τ dada se llama espacio de tolerancia. Por tanto, el espacio de tolerancia es un par (M, τ).
Ejemplo 4 . El espacio de tolerancia Sp se puede generalizar al caso infinito. Sea H un conjunto arbitrario. Si SH es la colección de todos los subconjuntos no vacíos del conjunto H, entonces la relación de tolerancia T sobre SH viene dada por la condición: X T Y si X∩Y ≠ ∅. La simetría y reflexividad de esta relación es obvia. El espacio SH se designa <H, T> y se denomina espacio de tolerancia "universal".
Ejemplo 5... Sea p un número natural. Denotamos por Bp el conjunto de todos los puntos del espacio p-dimensional cuyas coordenadas son iguales a 0 o 1. La tolerancia en Bp está especificada por la regla: xτy si xey contienen al menos un componente coincidente (coordenada). El número total de elementos en Bp es 2 r . Para cada elemento x = (a1, a2, ..., ap) del conjunto Bp, solo hay un elemento y = (1 - a1, 1 - a2, ..., 1 - ap) que no lo tolera.
Obviamente, Bp consta de todos los vértices del cubo p-dimensional.
Ejemplo 6 . Considere el espacio de tolerancia, cuyos componentes adquieren valores reales.
En particular, este es el conjunto de todos los puntos x = (a1, a2) en el plano cartesiano. La tolerancia de dos puntos significa que tienen al menos una coordenada. Esto significa que dos puntos tolerantes están en una vertical común o en una horizontal común.
Para otros valores de p, el espacio se puede interpretar como un conjunto de puntos en el espacio p-dimensional. En particular, cada elemento x puede considerarse una función numérica definida en el conjunto de números naturales {1, 2, 3, ...}, que asigna a cada número natural i: 1 ≤ i ≤ p un número real ai (una secuencia numérica finita). Entonces, la tolerancia de dos funciones xey significa que son iguales al menos en un punto.
Relaciones de orden parcial y su análisis
Los conjuntos ordenados son conjuntos con una relación de orden introducida. Definición . Un conjunto A y una relación de orden binario R en él (≤) se llama parcialmente ordenada si la relación cumple (como en BOE) tres condiciones (una condición es diferente):
- reflexividad ∀ x ∊ A (xRx); (antirreflexividad ∀ x ∊ A ¬ (xRx));
- antisimetría ∀ , y ∊ (Ry yRx → x = y);
- transitividad ∀ x, y, z ∊ A (xRy & yRz → xRz).
Con una actitud antirreflectante, surge un estricto orden parcial . El conjunto B (A) de todos los subconjuntos del conjunto A, ordenados por la inclusión de elementos, es un conjunto parcialmente ordenado (PN). El conjunto parcialmente ordenado (B (A), ⊆) a menudo se denomina booleano.
Un elemento x∊A POZA A cubre un elemento y∊A si x> y y no hay z∊A tal que x> z> y. Un par de elementos x, y∊A se llama comparable si x ≥ y o x ≤ y.
Si en PLA A cada par de sus elementos es comparable, entonces A se denomina conjunto o cadena linealmente ordenados . Si alguna plaga B consta solo de elementos incomparables entre sí, entonces el conjunto B se llama antichain
... Una cadena en PLAG A se llama saturada si no se puede anidar en ninguna otra cadena que no sea ella misma.
El antichain saturado se define de manera similar. Una cadena máxima (antichain) es una cadena (antichain) que contiene el número máximo de elementos.
Un elemento m de un PLM A se llama mínimo si no hay ningún elemento ∊ en distinto de my tal que ≤m. Un elemento M de una plaga A se llama máximo si no hay ningún elemento x "mayor" que M aparte de M y tal que x ≥ M.
Un elemento y∊A de una plaga A se llama máximo si ∀ x∊ A x ≤ y. El elemento y∊ A PLAG A se llama el más pequeñosi ∀ x∊A x ≥ y. Para los elementos más grandes y más pequeños, se acostumbra utilizar las designaciones 1 y 0, respectivamente. Se llaman fronteras universales. Cualquier plaga A tiene como máximo un elemento más pequeño y como máximo un elemento más grande. En el
PLA A se permiten varios elementos mínimos y varios máximos . Es conveniente representar el PLA A final con un diagrama de Hasse , que es un gráfico dirigido, sus vértices se distribuyen sobre los niveles del diagrama y corresponden a elementos de A, y cada arco se dirige hacia abajo y se dibuja si y solo si x∊A cubre el elemento y∊A.
No se dibujan arcos transitivos. Los niveles del gráfico Hasse contienen elementos del mismo rango, es decir, conectado con los elementos mínimos del PCM por caminos de igual longitud (según el número de arcos).
Sea B un subconjunto no vacío de PLA A, entonces un elemento x∊A se llama el límite superior exacto (denotado por sup A B) del conjunto B si x ≥ y para todo y∊B y si se sigue de la verdad de la relación z ≥ y para todo y∊B, que z ≥ x.
El límite inferior exacto (denotado por inf A B) de un conjunto B es un elemento x∊A si x ≤ y para todo y∊B y si la condición z ≤ y para todo y∊ B implica que z ≤ x.
Ejemplo 7 . Se
dan dos conjuntos numéricos finitos A = {0,1,2, ..., 21} y B = {6,7,10,11}.
CHUM (A, ≤) se muestra en la Fig. 2.26.
La colección B Δ de todos los límites superiores para se llama cono superior para el conjunto B. La colección ∇de todas las caras inferiores para B se llama cono inferior para B.

Cualquier subconjunto de PLA también es PLP con respecto al orden heredado. Si el conjunto contiene los elementos más grandes y / o más pequeños, entonces son el máximo (mínimo, respectivamente). Lo contrario no es cierto. Boolean tiene un único elemento más pequeño (Ø) y un único elemento más grande.
En el conjunto dado, el elemento más pequeño es cero (0) y coincide con el único elemento mínimo, y el elemento más grande no existe. Los elementos máximos son {19, 20, 21}. El límite superior exacto para B = {6,7,10,11} es el elemento 21 (este es el elemento más pequeño en el cono superior).
Situación general. Sea un conjunto cuya cardinalidad sea *******. De todas las relaciones binarias que son posibles en este conjunto, destaquemos las relaciones binarias de preferencia y las relaciones estrictas de orden parcial relacionadas.
Los órdenes parciales difieren de los órdenes parciales estrictos solo en que contienen elementos adicionales (en la representación matricial - diagonal) (ai, ai) = 1, i = 1 (1) n, y el número de esos y otros órdenes en el conjunto completo de relaciones lo mismo. Hasta ahora, no se han encontrado dependencias (fórmula, algoritmo) que permitan calcular y enumerar el número de órdenes parciales para cualquier n.
Diferentes autores han determinado y publicado los siguientes resultados mediante cálculo directo (Tabla 2.12).
Los experimentos computacionales del autor hicieron posible obtener no solo el número, sino también la forma (representación) de órdenes parciales a diferentes potencias del multiplicador-portador de relaciones. El impresor se atragantó con la impresión de listas tan grandes, pero no solo la belleza requiere sacrificios, la ciencia tampoco los rechaza.

La tabla 2.12 muestra: n = | A | - la cardinalidad del portador de set; la segunda línea es el número de todas las relaciones binarias en el conjunto A; y más
| En (n) | - el número de clases de relaciones no isomórficas;
| (n) | - el número de relaciones de orden parcial;
| Gn (n) | - el número de clases de relaciones de orden parcial no isomórficas;
| Gl (n) | = n! - el número de relaciones de orden lineal.
Como puede ver, en la tabla para n pequeño, por ejemplo, G (n = 4), solo hay 219, se dan datos, cuyos valores crecen muy rápidamente al aumentar n, lo que complica significativamente su análisis directo cuantitativo (y cualitativo), incluso con una computadora.
La siguiente tabla ilustra la posibilidad de generar Γ (n = 4) de todos los órdenes parciales a partir de la intersección de cada uno con cada orden parcial lineal. Pero en esta situación, surgen redundantes (repetitivos), que para n pequeños se pueden cortar manualmente (recalcular). Resultan 300 matrices, pero solo hay 219 PL entre ellas, no se han obtenido fórmulas generales. A nivel mundial, la situación es similar, aunque no he visto ninguna publicación sobre las transferencias de PLM por parte de autores occidentales. Nuestros algoritmos son completamente originales y pioneros.
Daré un posible esquema para resolver el problema de enumerar los elementos del espacio de órdenes parciales (n = 4).

El conjunto de órdenes parciales estrictos en el ordenamiento lexicográfico de órdenes lineales (n = 4) se genera por su intersección mutua.


Varias definiciones importantes de matemáticas, para conceptos que a menudo se encuentran en textos.
Definición . Un intervalo cerrado es un conjunto de la forma {x: a ≤ x ≤ b}; un intervalo abierto no es cerrado, y un intervalo semiabierto, es decir, un conjunto de la forma {x: a <x ≤ b}, donde a <b, o de la forma {x: a ≤ x <b} no es ni abierto ni cerrado.
Definición . El límite de un intervalo arbitrario de una línea real en la topología habitual de números reales consta solo de los extremos de este intervalo, independientemente de si este intervalo es abierto, cerrado o medio abierto. El límite del conjunto de números racionales, así como el límite del conjunto de todos los números irracionales, es el conjunto completo de números reales.
Definición... Todo conjunto ordenado linealmente, en cualquier subconjunto no vacío del que exista el elemento más pequeño, se llama bien ordenado.
Definición . Una familia R se llama cadena (a veces una torre, un nido) si y solo si, para cualquiera de sus elementos A y B, A ⊂ B o B ⊂ A. Esta condición es equivalente a la afirmación de que la familia R está ordenada linealmente por inclusión o, en la terminología aceptada - que la familia R junto con la relación de inclusión es una cadena.
P r y n c y p m a to s y m al n acerca de s t y H a u s d o r f a Para cualquier familia de conjuntos A y cualquier nido R formado por elementos de la familia A, hay un nido máximo M en A que contiene R.
Un teorema importante sobre conjuntos y sus familias (J.L. Kelly "Topología general" p. 55).
Teorema. (a) PRINTSIpMakSIMALN sobre ELEMENT. Existe un elemento máximo en la familia A de un conjunto si, para cada nido en A, hay un elemento en A que contiene un elemento arbitrario de este nido.
(b) PRINTSIpMINIMALNO ELEMENT. El elemento más pequeño en una familia A existe si, para cada nido en A, hay un elemento en A que está contenido en cada elemento de este nido.
(c) Lema T yuk y. Cada familia de conjuntos de carácter finito tiene un elemento máximo.
(d) LEMMA KURATOVSKOGO. Cada cadena en un conjunto (parcialmente) ordenado está contenida en alguna cadena máxima.
(e) Lema de Tson. Si cada cadena de algún conjunto parcialmente ordenado está acotada desde arriba, entonces este conjunto tiene un elemento máximo.
(f) A a s y o m y una elección. Sea Xα un conjunto no vacío para cada elemento a del conjunto de índices A. Entonces existe una función c en A tal que c (a) ∊ Xα para cada a de A.
(g) Postulado Tserm elo. Para cualquier familia A de conjuntos no vacíos disjuntos, hay un conjunto C tal que AUC para cada A de A consta exactamente de un punto.
(h) IMPRESIONES y P en el orden de entrega completo. Cada juego se puede pedir completamente.