😼 🎩 👩‍👩‍👧 Espacios vectoriales ❗️ 🍧 🚢

Al realizar una investigación científica y aplicada, se suelen crear modelos en los que se consideran puntos y / o vectores de determinados espacios. Por ejemplo, los modelos de cifrado de curva elíptica utilizan espacios afines y proyectivos. Recurren a las proyectivas cuando es necesario agilizar los cálculos, ya que en las fórmulas de manipulación de los puntos de una curva elíptica derivadas en el marco del espacio proyectivo, no hay operación de división por coordenada, que no puede ser eludida en el caso de un espacio afín .

La operación de división es solo una de las operaciones más "costosas". El hecho es que en los campos algebraicos, y en consecuencia en los grupos, no hay ninguna operación de división y la salida (cuando es imposible no dividir) es que la operación de división se reemplaza por la multiplicación, pero no se multiplica por la coordenada en sí, sino por su valor inverso. ... De esto se deduce que primero se debe involucrar el algoritmo GCD euclidiano extendido y algo más. En resumen, no todo es tan simple como lo describen los autores de la mayoría de las publicaciones sobre la ECC. Casi todo lo que se ha publicado sobre este tema y no solo en Internet me resulta familiar. No solo los autores no son competentes y se dedican a la profanación, los evaluadores de estas publicaciones agregan autores en los comentarios, es decir, no ven lagunas ni errores obvios. Sobre un artículo normal, escriben que ya es el número 100500 y no tiene ningún efecto.Así se ordena todo en Habré, el análisis de las publicaciones es enorme, pero no la calidad del contenido. No hay nada que objetar aquí: la publicidad es el motor de los negocios.

Espacio vectorial lineal

El estudio y descripción de los fenómenos del mundo circundante nos lleva necesariamente a la introducción y uso de una serie de conceptos como puntos, números, espacios, rectas, planos, sistemas de coordenadas, vectores, conjuntos, etc.

Sea r _<3>= <r1, r2, r3> vector del espacio tridimensional, especifica la posición de una partícula (punto) con respecto al origen. Si consideramos N elementos, entonces la descripción de su posición requiere especificar coordenadas 3 ∙ N, que pueden considerarse como las coordenadas de algún vector en el espacio tridimensional. Si consideramos las funciones continuas y sus colecciones, llegamos a espacios cuya dimensión es igual al infinito. En la práctica, a menudo se limitan a usar solo el subespacio de un espacio funcional de coordenadas de dimensión infinita que tiene un número finito de dimensiones.

Ejemplo 1 . La serie de Fourier es un ejemplo de uso del espacio funcional. Considere la expansión de una función arbitraria en una serie de Fourier

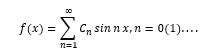
Puede interpretarse como la expansión del "vector" f (x) en un conjunto infinito de vectores de base "ortogonales" sinnx.

Este es un ejemplo de abstracción y extensión del concepto de vector a un número infinito de dimensiones. De hecho, se sabe que para -π≤x≤π

La esencia de una consideración adicional no se verá afectada si nos abstraemos de la dimensión del espacio vectorial abstracto, ya sea 3, 3N o infinito, aunque para aplicaciones prácticas, los campos de dimensión finita y los espacios vectoriales son de mayor interés.

Un conjunto de vectores r1, r2,… se llamará espacio vectorial lineal L si la suma de dos de sus elementos también está en este conjunto y si el resultado de multiplicar un elemento por un número C también se incluye en este conjunto. Hagamos una reserva de inmediato de que los valores del número C se pueden seleccionar de un conjunto numérico bien definido F, el campo de residuos módulo un número primo p, que se considera adjunto a

L.Ejemplo 2 . Un conjunto de 8 vectores formado por n = números binarios de 5 bits

r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 forma el espacio vectorial L si los números C є {0,1}. Este pequeño ejemplo le permite verificar la manifestación de las propiedades de un espacio vectorial incluidas en su definición.

La suma de estos vectores se realiza bit a bit en módulo dos, es decir, sin transferir unos al bit más significativo. Tenga en cuenta que si todos los C son reales (en el caso general, C pertenecen al campo de los números complejos), entonces el espacio vectorial se llama real.

Formalmente, los axiomas del espacio vectorial se escriben de la siguiente manera:

r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L - conmutatividad de adición y cierre;

(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 - asociatividad de adición;

ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L - existencia de un elemento neutro;

ri + (- ri) = r0, para ∀i hay un vector opuesto (-ri) є L;

1 ∙ ri = ri ∙ 1 = ri existencia de una unidad de multiplicación;

α (β ∙ ri) = (α ∙ β) ∙ ri; α, β, 1, 0 son elementos del campo numérico F, ri є L; la multiplicación por escalares es asociativa; el resultado de la multiplicación pertenece a L;

(α + β) ri = α ∙ ri + β ∙ ri; para ∀i, ri є L, α, β son escalares;

a (ri + rj) = ari + arj para todo a, ri, rj є L;

a ∙ 0 = 0, 0 ∙ ri = 0; (-1) ∙ ri = - ri.

Dimensión y base del espacio vectorial

Al estudiar los espacios vectoriales, es de interés aclarar cuestiones como el número de vectores que forman el espacio completo; cuál es la dimensión del espacio; ¿Cuál es el conjunto de vectores más pequeño, aplicándole la operación de suma y multiplicación por un número, que permite formar todos los vectores en el espacio? Estas preguntas son fundamentales y no se pueden ignorar, ya que sin respuestas a ellas se pierde la claridad de percepción de todo lo demás que conforma la teoría de los espacios vectoriales.

Resultó que la dimensión del espacio está estrechamente relacionada con la dependencia lineal de los vectores y con el número de vectores linealmente independientes que se pueden seleccionar en el espacio en estudio de muchas formas.

Independencia lineal de vectores

Un conjunto de vectores r1, r2, r3 ... r de L se llama linealmente independiente si para ellos la relación

se satisface solo bajo la condición de igualdad simultánea

с_{1} = с_{2} = \dots = с_{р} = 0

$_1=_2=…=_=0$ ...

Todos

с_{k}

$_k$ , k = 1 (1) p, pertenecen al campo de residuo numérico módulo dos

F = {0, 1}.

Si en algún espacio vectorial L se puede elegir un conjunto de p vectores para los cuales la relación

c_{1} r_{1} + c_{2} r_{2} + . . . + c_{p} r_{p} = 0

$c_1 r_1+c_2 r_2+...+c_p r_p=0$ se cumple, siempre que no todos

с_{k} = 0

$_k = 0$ simultáneamente, es decir resultó ser posible seleccionar el conjunto

с_{k}

$_k$ , k = 1 (1) , entre los cuales hay unos distintos de cero, entonces dichos vectores

r_{i}

$r_i$ se llaman linealmente dependientes.

Ejemplo 3 . Dos vectores en el avión.

е_{1}

$_1$ = <0, 1> ^T y

е_{2}

$_2$ = <1, 0> ^T son linealmente independientes, ya que en la relación (T-transposición)

es imposible recoger un par de números

с_{1}, с_{2}

$_1, _2$ coeficientes no iguales a cero al mismo tiempo para que se satisfaga la relación.

Tres vectores

е_{1}

$_1$ = <0, 1> ^T ,

е_{2}

$_2$ = <1, 0> ^T ,

е_{3}

$_3$ = <1, 1> ^T forman un sistema de vectores linealmente dependientes, ya que en la relación

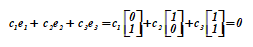
la igualdad se puede asegurar eligiendo los coeficientes

с_{1} = с_{2} = 1, с_{3} = - 1

$_1 = _2 = 1, _3 = –1$ no igual a cero al mismo tiempo. Además, el vector

e_{3} = е_{1} + е_{2}

$e_3 = _1 + _2$ es una función

е_{1}

$_1$ y

е_{2}

$_2$ (su suma), que indica la dependencia

e_{3}

$e_3$ desde

е_{1}

$_1$ y

е_{2}

$_2$ ... La prueba del caso general es la siguiente.

Deje que al menos uno de los valores

с_{k}

$_k$ , k = 1 (1) p, por ejemplo,

с_{р} \neq 0

$_ ≠ 0$ , y la relación queda satisfecha. Esto significa que los vectores

r_{k}

$r_k$ , k = 1 (1) , son linealmente dependientes

Separemos explícitamente el vector r

Se dice que el vector r _p es una combinación lineal de vectores

r_{1}, r_{2} \dots r_{р} - 1

$r_1, r_2… r_-1$ o r _{p a} través de los vectores restantes se expresa de manera lineal, es decir r _p depende linealmente de los demás. Él es su función.

En un plano bidimensional, cualesquiera tres vectores son linealmente dependientes, pero cualesquiera dos vectores no colineales son independientes. En el espacio 3D, cualesquiera tres vectores no coplanares son linealmente independientes, pero cualesquiera cuatro vectores siempre son linealmente dependientes.

Dependencia / independencia de la población {

e_{1}, e_{2}, e_{3}, . . ., e_{n}

${e_1, e_2, e_3, ..., e_n}$ } los vectores a menudo se determinan calculando el determinante de la matriz de Gram (sus filas son los productos escalares de nuestros vectores). Si el determinante es cero, hay vectores dependientes entre los vectores; si el determinante es distinto de cero, los vectores de la matriz son independientes.

El determinante de Gram (Gramian) del sistema vectorial

e_{1}, e_{2}, \dots, e_{n} e_{1}, e_{2}, \dots, e_{n}

${\displaystyle \mathbf {e} _{1},\;\mathbf {e} _{2},\;\ldots ,\mathbf {e} _{n}}\mathbf{e}_1,\;\mathbf{e}_2,\;\ldots,\mathbf{e}_n$

el determinante de la matriz de Gram de este sistema se llama en el espacio euclidiano:

| \begin{matrix} ⟨ e_{1}, e_{1} ⟩ & ⟨ e_{1}, e_{2} ⟩ & \dots & ⟨ e_{1}, e_{n} ⟩ \\ ⟨ e_{2}, e_{1} ⟩ & ⟨ e_{2}, e_{2} ⟩ & \dots & ⟨ e_{2}, e_{n} ⟩ \\ \dots & \dots & \dots & \dots \\ ⟨ e_{n}, e_{1} ⟩ & ⟨ e_{n}, e_{2} ⟩ & \dots & ⟨ e_{n}, e_{n} ⟩ \end{matrix} |, | \begin{matrix} ⟨ e_{1}, e_{1} ⟩ & ⟨ e_{1}, e_{2} ⟩ & \dots & ⟨ e_{1}, e_{n} ⟩ \\ ⟨ e_{2}, e_{1} ⟩ & ⟨ e_{2}, e_{2} ⟩ & \dots & ⟨ e_{2}, e_{n} ⟩ \\ \dots & \dots & \dots & \dots \\ ⟨ e_{n}, e_{1} ⟩ & ⟨ e_{n}, e_{2} ⟩ & \dots & ⟨ e_{n}, e_{n} ⟩ \end{matrix} |,

${\displaystyle {\begin{vmatrix}\langle e_{1},\;e_{1}\rangle &\langle e_{1},\;e_{2}\rangle &\ldots &\langle e_{1},\;e_{n}\rangle \\\langle e_{2},\;e_{1}\rangle &\langle e_{2},\;e_{2}\rangle &\ldots &\langle e_{2},\;e_{n}\rangle \\\ldots &\ldots &\ldots &\ldots \\\langle e_{n},\;e_{1}\rangle &\langle e_{n},\;e_{2}\rangle &\ldots &\langle e_{n},\;e_{n}\rangle \\\end{vmatrix}},}\begin{vmatrix} \langle e_1,\;e_1\rangle & \langle e_1,\;e_2\rangle & \ldots & \langle e_1,\;e_n\rangle \\ \langle e_2,\;e_1\rangle & \langle e_2,\;e_2\rangle & \ldots & \langle e_2,\;e_n\rangle \\ \ldots & \ldots & \ldots & \ldots \\ \langle e_n,\;e_1\rangle & \langle e_n,\;e_2\rangle & \ldots & \langle e_n,\;e_n\rangle \\ \end{vmatrix},$

Dónde

⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩

${\displaystyle \langle e_{i},\;e_{j}\rangle }\langle e_i,\;e_j\rangle{\displaystyle \langle e_{i},\;e_{j}\rangle }\langle e_i,\;e_j\rangle$ - producto escalar de vectores

e_{i} e_{i}

${\displaystyle \mathbf {e} _{i}}\mathbf{e}_i$ y

e_{j} e_{j}

${\displaystyle \mathbf {e} _{j}}\mathbf{e}_j$ ...

Dimensión y base de un espacio vectorial

La dimensión s = d (L) de un espacio L se define como el mayor número de vectores en L que forman un conjunto linealmente independiente. La dimensión no es el número de vectores en L, que puede ser infinito, y no el número de componentes vectoriales.

Los espacios de dimensión finita s ≠ ∞ se denominan de dimensión finita si

s = ∞, de dimensión infinita.

La respuesta a la pregunta sobre el número mínimo y la composición de vectores que garantizan la generación de todos los vectores en un espacio vectorial lineal es la siguiente afirmación.

Cualquier colección de s de vectores linealmente independientes en el espacio L forma sus bases y c. Esto se sigue del hecho de que cualquier vector

r_{k}

$r_k$ El espacio vectorial lineal L de dimensión s se puede representar de una manera única como una combinación lineal de vectores básicos.

Fijamos y denotamos por el símbolo

е_{i}

$_i$ , i = 1 (1) s, es una de las colecciones que forman la base del espacio L.Entonces

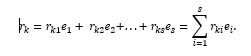
Los números r _ki , i = 1 (1) s se denominan coordenadas del vector

r_{k}

$r_k$ en la base

е_{i}

$_i$ , i = 1 (1) s, y r _ki = (

е_{i}

$_i$ ,

r_{k}

$r_k$ ).

Demostremos la singularidad de la representación

r_{k}

$r_k$ ... Obviamente, el set

e_{1}, e_{2}, . . ., e_{s}

$e_1,e_2,...,e_s$ ,

r_{k}

$r_k$ es dependiente, ya que

е_{i}

$_i$ , i = 1 (1) s es una base. En otras palabras, existen tales

с_{1}, с_{2} . . . с_{s}, c_{k}

$_1, _2... _s, c_k$ no simultáneamente igual a cero, que

c_{1} \cdot e_{1} + c_{2} \cdot e_{2} + . . . + c_{s} \cdot e_{s} + c_{k} \cdot r_{k} = 0

$c_1·e_1 + c_2·e_2 + ...+ c_s·e_s + c_k·r_k = 0$ ...

Además, deja

c_{k} \neq 0

$c_k ≠ 0$ porque si

c_{k} = 0

$c_k = 0$ , entonces al menos uno de

с_{1}, с_{2}, . . ., с_{s}

$_1, _2 , ... , _s$ , sería distinto de cero y luego vectores

e_{i}

$e_i$ , i = 1 (1) s, sería linealmente dependiente, lo cual es imposible, ya que esta es una base. Por consiguiente,

Asumiendo

, tendremos

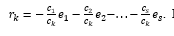
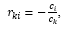
Usando el método de prueba "por contradicción", asumimos que la representación escrita

r_{k}

$r_k$ no el único en esta base y hay algo más

Luego anotamos la diferencia de representaciones, que, por supuesto, se expresa como

Obviamente, los lados derecho e izquierdo son iguales, pero el izquierdo representa la diferencia del vector consigo mismo, es decir, es igual a cero. En consecuencia, el lado derecho también es cero. Vectores

е_{i}

$_i$ , i = 1 (1) s son linealmente independientes, por lo que todos los coeficientes para ellos solo pueden ser cero. De esto obtenemos eso

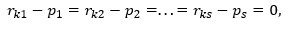
y esto es posible solo para

La elección de la base. Ortonormalidad

Los vectores se denominan normalizados si la longitud de cada uno de ellos es igual a uno. Esto se puede lograr aplicando el procedimiento de normalización a vectores arbitrarios.

Los vectores se denominan ortogonales si son perpendiculares entre sí. Estos vectores se pueden obtener aplicando un procedimiento de ortogonalización a cada uno de ellos. Si se satisfacen ambas propiedades para un conjunto de vectores, los vectores se denominan ortonormales.

La necesidad de considerar bases ortonormales se debe a la necesidad de utilizar transformaciones rápidas de funciones unidimensionales y multidimensionales. Las tareas de dicho procesamiento surgen en el estudio de códigos que codifican mensajes de información en redes de comunicación de diversos fines, en el estudio de imágenes obtenidas

a través de dispositivos automáticos y automatizados, en una serie de otras áreas utilizando representaciones digitales de información.

Definición. La colección de n vectores linealmente independientes de un

espacio vectorial V de n dimensiones se llama su base.

Teorema . Cada vector x de un espacio vectorial lineal n-dimensional V se puede representar, además, de una manera única, en forma de una combinación lineal de vectores base. El espacio vectorial V sobre el campo F tiene las siguientes propiedades:

0 x = 0 (0 en el lado izquierdo de la igualdad es un elemento neutral del grupo aditivo del campo F; 0 en el lado derecho de la igualdad es un elemento del espacio V, que es un elemento unitario neutral del grupo aditivo V, llamado vector cero );

(- 1) · x = –x; –1є F; x є V; –X є V;

Si α x = 0єV, entonces para x ≠ 0 siempre α = 0.

Sea Vn (F) el conjunto de todas las secuencias (x1, x2, ..., xn) de longitud n con componentes del campo F, es decir, Vn (F) = {x, tal que x = (x1, x2, ..., xn), xi є F;

i = 1 (1) n}.

La suma y la multiplicación por un escalar se definen como sigue:

x + y = (x1 + y1, x2 + y2,…, xn + yn);

α x = (α x1, α x2,…, α xn), donde y = (y1, y2,…, yn),

entonces Vn (F) es un espacio vectorial sobre el campo F.

Ejemplo 4 . En el espacio vectorial r = 00000, r1 = 10101, r2 = 11010, r3 = 10101 sobre el campo F2 = {0,1} determinar su dimensión y base.

Decisión. Formemos una tabla de suma de vectores de un espacio vectorial lineal

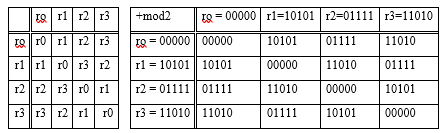
En este espacio vectorial V = {ro, r1, r2, r3} cada vector tiene a sí mismo como su opuesto. Dos vectores cualesquiera, excluyendo r®, son linealmente independientes, lo cual es fácil de verificar

c1 · r1 + c2 · r2 = 0; c1 r1 + c3 r3 = 0; c2 r2 + c3 r3 = 0;

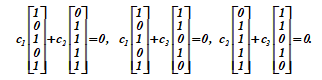
Cada una de las tres relaciones es válida solo para valores cero simultáneos de los pares de coeficientes ci, cj є {0,1}.

Cuando se consideran simultáneamente tres vectores distintos de cero, uno de ellos es siempre la suma de los otros dos o es igual a sí mismo, y r1 + r2 + r3 = r.

Por tanto, la dimensión del espacio vectorial lineal considerado es igual a dos s = 2, d (L) = s = 2, aunque cada uno de los vectores tiene cinco componentes. La base del espacio es la colección (r1, r2). Puede utilizar el par (r1, r3) como base.

Teórica y prácticamente, la cuestión de describir el espacio vectorial es importante. Resulta que cualquier conjunto de vectores base puede verse como filas de alguna matriz G, llamada matriz generadora del espacio vectorial. Cualquier vector de este espacio se puede representar como una combinación lineal de filas de la matriz G ( como, por ejemplo, aquí ).

Si la dimensión del espacio vectorial es ky es igual al número de filas de la matriz G, el rango de la matriz G, entonces obviamente hay k coeficientes con q valores diferentes para generar todas las combinaciones lineales posibles de las filas de la matriz. Además, el espacio vectorial L contiene q ^k vectores.

El conjunto de todos los vectores de ℤpn con operaciones de suma de vectores y multiplicación de un vector por un escalar de ℤp es un espacio vectorial lineal.

Definición . Un subconjunto W de un espacio vectorial V que satisface las condiciones:

Si w1, w2 є W, entonces w1 + w2 є W,

Para cualquier α є F y w є W, el elemento αw є W es en

sí mismo un espacio vectorial sobre el campo F y se denomina subespacio del espacio vectorial V.

Sea V un espacio vectorial sobre un campo F y un conjunto W ⊆ V. El conjunto W es un subespacio del espacio V si W con respecto a las operaciones lineales definidas en V es un espacio vectorial lineal.

Mesa. Características de los espacios vectoriales

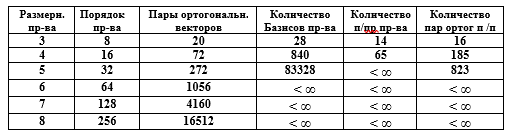
La compacidad de la representación matricial de un espacio vectorial es obvia. Por ejemplo, especificar L vectores de números binarios de 50 bits, entre los cuales 30 vectores forman la base del espacio vectorial, requiere la formación de la matriz G [30,50], y el número de vectores descrito excede 10 ⁹ , lo que parece irrazonable en la notación de elementos.

Todas las bases de cualquier espacio L están divididas por el subgrupo P de matrices no degeneradas con det G> 0 en dos clases. Uno de ellos (arbitrariamente) se llama clase con bases orientadas positivamente (derechas), la otra clase contiene bases izquierdas.

En este caso, dicen que se da una orientación en el espacio. Después de eso, cualquier base es un conjunto ordenado de vectores.

Si la numeración de dos vectores se cambia en la base correcta, entonces la base se convertirá en la izquierda. Esto se debe al hecho de que dos filas en la matriz G se intercambian, por lo tanto, el determinante detG cambiará de signo.

Norma y producto escalar de vectores

Después de resolver las preguntas sobre encontrar la base de un espacio vectorial lineal, sobre la generación de todos los elementos de este espacio y sobre la representación de cualquier elemento y el propio espacio vectorial a través de los vectores base, podemos plantear el problema de medir en este espacio las distancias entre elementos, ángulos entre vectores, valores de componentes vectoriales. , las longitudes de los propios vectores.

Un espacio vectorial real o complejo L se llama espacio vectorial normalizado si cada vector r en él se puede asociar con un número real || r || - módulo vectorial, norma. Un vector unitario es un vector cuya norma es uno. El vector cero tiene componentes cero.

Definición... Un espacio vectorial se llama unitario si en él se define una operación binaria que asigna un escalar a cada par ri, rj de vectores de L. Entre paréntesis (ri, rj) se escribe (denota) el escalar o producto interno de ri y rj, y

1. (ri, rj) = ri ∙ rj;

2. (ri, rj) = (ri ∙ rj) *, donde * indica conjugación compleja o simetría hermitiana;

3. (ri, rj) = (ri ∙ rj) - ley asociativa;

4. (ri + rj, rk) = (ri ∙ rk) + (rj ∙ rk) - ley distributiva;

5. (ri, rk) ≥ 0 y de (ri, rj) = 0 se sigue ri = 0.

Definición . El valor positivo de la raíz cuadrada

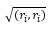se llama norma (o longitud, módulo) del vector ri. Si

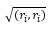= 1, entonces el vector ri se llama normalizado...

Dos vectores ri, rj del espacio vectorial unitario L son mutuamente ortogonales si su producto escalar es igual a cero, es decir, (ri, rj) = 0.

Para s = 3 en un espacio vectorial lineal, es conveniente elegir tres vectores mutuamente perpendiculares como base. Esta elección simplifica enormemente una serie de dependencias y cálculos. El mismo principio de ortogonalidad se usa al elegir una base en espacios y otras dimensiones s> 3. El uso de la operación introducida del producto escalar de vectores brinda la posibilidad de tal elección.

Se logran ventajas aún mayores al elegir como base del espacio vectorial de vectores normalizados ortogonales: la base ortonormal... A menos que se indique lo contrario, siempre asumiremos que la base ei, i = 1 (1) s se elige de esta manera, es decir

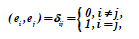
, donde ij es el símbolo de Kronecker (1823-1891).

En los espacios vectoriales unitarios, esta elección siempre es realizable. Demostremos la viabilidad de tal elección.

Definición. Sea S = {v1, v2,…, vn} un subconjunto finito de un espacio vectorial V sobre un campo F.

Una combinación lineal de vectores de S es una expresión de la forma a1 ∙ v1 + a2 ∙ v2 +… + an ∙ vn, donde cada ai ∊ F.

La envolvente para el conjunto S (notación {S}) es el conjunto de todas las combinaciones lineales de vectores de S. La envolvente de S es un subespacio de V.

Si U es un espacio en V, entonces U está dividido por S (S contrae U) si {S} = U.

El conjunto de vectores S es linealmente dependiente de F si hay escalares a1, a2, ..., an en F, no todos ceros para los cuales a1 ∙ v1 + a2 ∙ v2 +… + an ∙ vn = 0. Si no existen tales escalares, entonces el conjunto de vectores S linealmente independientes sobre F.

Si un espacio vectorial V está atravesado por un sistema linealmente independiente de vectores S (o el sistema S contrae el espacio V), entonces el sistema S se denomina base para V.

Reducción de una base arbitraria a forma ortonormal

Deje que el espacio V tenga una base no ortonormal ē _i , i = 1 (1) s. Denotamos la norma de cada vector base con el símbolo

Se conoce la siguiente declaración [11]. Si ē _i , i = 1 (1) s es un sistema arbitrario finito o contable de vectores linealmente independientes en un espacio vectorial unitario, entonces existe un sistema ortonormal ē _i , i = 1 (1) s, que genera el mismo espacio lineal (variedad).

El procedimiento para reducir la base a una forma ortonormalizada se basa en el proceso de ortogonalización de Gram-Schmidt, que a su vez se implementa mediante fórmulas recurrentes

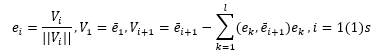
En forma expandida, el algoritmo de ortogonalización y normalización de bases contiene las siguientes condiciones:

Dividir el vector ē ₁ por su norma; obtenemos el vector normalizado ē _i = ē ₁ / (|| ē ₁ ||);

Formamos V2 = ē ₂ - (ē ₁ , ē ₂ ) e ₁ y lo normalizamos, obtenemos e ₂ . Es claro que entonces

(e1, e2) ~ (e1, e2) - (e1, e ₂ ) (e1, e1) = 0;

Construyendo V3 = ē ₃ - (e1, ē ₃ ) e1 - (e2, ē ₃ ) e2 y normalizándolo, obtenemos e3.

Para ello, inmediatamente tenemos (e1, e3) = (e2, e3) = 0.

Continuando con este proceso, obtenemos un conjunto ortonormal ē _i , i = 1 (1) s. Este conjunto contiene vectores linealmente independientes ya que todos son mutuamente ortogonales.

Asegurémonos de esto. Deja que la relación

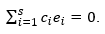
Si el conjunto ē _i , i = 1 (1) s es dependiente, entonces al menos un coeficiente cj no es igual a cero cj ≠ 0.

Multiplicando ambos lados de la razón por ej, obtenemos

(ej, c1 ∙ e1) + (ej, c2 ∙ e2) + ... + (ej, cj ∙ ej) +… + (ej, cs ∙ rs) = 0.

Cada sumando en la suma es igual a cero como el producto escalar de vectores ortogonales, excepto para (ej, cj ∙ ej), que es igual a cero en condición. Pero en este término

(ej, ej) = 1 ≠ 0, por lo tanto, solo cj puede ser cero.

Por tanto, la suposición de que cj ≠ 0 no es cierta y la colección es linealmente independiente.

Ejemplo 5 . Se da una base de un espacio vectorial tridimensional:

{<-1, 2, 3, 0>, <0, 1, 2, 1>, <2, -1, -1,1>}.

El producto escalar se define por la relación:

(<x1, x2, x3, x4>, <y1, y2, y3, y4>) = x1 ∙ y1 + x2 ∙ y2 + x3 ∙ y3 + x4 ∙ y4.

Utilizando el procedimiento de ortogonalización de Gram-Schmidt, obtenemos un sistema de vectores:

1 = <-1, 2, 3, 0>; a2 = <0, 1, 2, 1> -4 <-1, 2, 3,0> / 7 = <4, -1, 2, 7> / 7;

a3 = <2, -1, -1, 1> + ½ <-1, 2, 3, 0> - <4, -1, 2, 7> / 5 = <7, 2, 1, -4> / diez.

(a1, a2) = (1 + 4 + 9 + 0) = 14;

a1 ^E = a1 / √14;

a2- (a1 ^E , a2) ∙ a1 ^E = a2- (8 / √14) (a1 / √14) = a2 - 4 ∙ a1 / 7;

Se invita al lector a procesar el tercer vector de forma independiente.

Los vectores normalizados toman la forma:

a1 ^E = a1 / √14;

a2 ^E = <4, -1, 2, 7> / √70;

a3 ^E = <7, 2, 1, -4>/ √70;

A continuación, en el ejemplo 6, se muestra un proceso de cálculo detallado y detallado para obtener una base ortonormal a partir de una simple (tomada al azar).

Ejemplo 6 . Reducir la base dada del espacio vectorial lineal a forma ortonormal.

Dado: vectores base

Subespacios de espacios vectoriales

Estructura del espacio vectorial La

representación de objetos (cuerpos) en espacios multidimensionales es una tarea muy difícil. Entonces, un cubo de cuatro dimensiones tiene cubos tridimensionales ordinarios como caras, y se puede construir un despliegue de un cubo de cuatro dimensiones en un espacio tridimensional. Hasta cierto punto, las "imágenes" y la claridad de un objeto o sus partes contribuyen a su estudio más exitoso.

Lo anterior nos permite asumir que los espacios vectoriales se pueden desmembrar de alguna manera, para singularizar partes en ellos, llamados subespacios. Obviamente, la consideración de espacios y objetos multidimensionales y especialmente de dimensión infinita en ellos nos priva de la claridad de las representaciones, lo que hace muy difícil estudiar objetos en tales dimensiones.

espacios. Incluso cuestiones aparentemente simples como las características cuantitativas de los elementos de los poliedros (el número de vértices, aristas, caras, etc.) en estos espacios están lejos de estar completamente resueltas.

Una forma constructiva de estudiar tales objetos es seleccionar sus elementos (por ejemplo, aristas, caras) y describirlos en espacios de menor dimensión. Entonces, un cubo de cuatro dimensiones tiene cubos tridimensionales ordinarios como caras, y se puede construir un despliegue de un cubo de cuatro dimensiones en un espacio tridimensional. Hasta cierto punto, las

"imágenes" y la claridad del objeto o sus partes contribuyen a su estudio más exitoso.

Si L es una extensión del campo K, entonces L puede considerarse como un espacio vectorial (o lineal) sobre K. Los elementos del campo L (es decir, vectores) forman un grupo abeliano por adición. Además, cada "vector" a є L se puede multiplicar por un "escalar" r є K, y el producto ra pertenece de nuevo a L (aquí ra es simplemente el producto en el sentido del campo L operación de los elementos r y a de este campo). Las leyes también sostienen

r ∙ (a + b) = r ∙ a + r ∙ b, (r + s) ∙ a = r ∙ a + r ∙ s, (r ∙ s) ∙ a = r ∙ (s ∙ a) y 1 ∙ a = a, donde r, s є K, a, b є L.

Lo anterior nos permite suponer que los espacios vectoriales se pueden desmembrar de alguna forma, para singularizar partes en ellos, llamados subespacios. Obviamente, el principal resultado de este enfoque es reducir la dimensión de los subespacios asignados. Supongamos que los subespacios L1 y L2 se distinguen en un espacio lineal vectorial L. Como base para L1, se elige un conjunto más pequeño ei, i = 1 (1) s1, s1 <s, que en el original L.

Los vectores base restantes generan otro subespacio L2, llamado el “complemento ortogonal” del subespacio L1. Usaremos la notación L = L1 + L2. No significa que todos los vectores del espacio L pertenezcan a L1 o L2, sino que cualquier vector de L puede representarse como la suma de un vector de L1 y un vector ortogonal de L2.

No es el conjunto de vectores del espacio vectorial L el que se divide, sino la dimensión d (L) y el conjunto de vectores base. Así, el subespacio L1 de un espacio vectorial L es el conjunto L1 de sus elementos (de menor dimensión), que a su vez es un espacio vectorial con respecto a las operaciones de suma y multiplicación por un número introducido en L.

Cada subespacio de vector lineal Li - contiene un vector cero y, junto con cualquiera de sus vectores, contiene todas sus combinaciones lineales. La dimensión de cualquier subespacio lineal no excede la dimensión del propio espacio original.

Ejemplo 7.En el espacio tridimensional ordinario, los subespacios son todas líneas rectas (dimensión s = 1) líneas, planos (dimensión s = 2) que pasan por el origen. En el espacio n de polinomios de grado como máximo n, los subespacios son, por ejemplo, todos k para k <n, ya que sumando y multiplicando por números polinomios de grado como máximo k, obtendremos nuevamente los mismos polinomios.

Sin embargo, cada uno de los espacios Pn está contenido como subespacios en el espacio P de todos los polinomios con coeficientes reales, y este último es un subespacio del espacio C de funciones continuas.

Las matrices del mismo tipo sobre el campo de números reales también forman un espacio vectorial lineal, ya que satisfacen todos los axiomas de los espacios vectoriales. El espacio vectorial L2 de conjuntos de longitud n, cada uno de los cuales es ortogonal al subespacio L1 de conjuntos de longitud n, forma un subespacio L2, llamado espacio cero para L1. En otras palabras, cada vector de L2 es ortogonal a cada vector de L1 y viceversa.

Tanto los subespacios L1 como L2 son subespacios del espacio vectorial L de conjuntos de longitud N. En la teoría de la codificación [4], cada uno de los subespacios L1 y L2 genera un código lineal dual al código generado por otros subespacios. Si L1 es un código (n, k), entonces L2 es un código (n, n - k). Si un código es un espacio vectorial de filas de alguna matriz, entonces su código dual es el espacio cero de esta matriz y viceversa.

Un tema importante en el estudio de los espacios vectoriales Vn es el establecimiento de su estructura (estructura). Es decir, son de interés los elementos, sus colecciones (subespacios de dimensión 1 <k <n), así como sus relaciones (ordenamiento, jerarquización, etc.). Suponemos que un espacio vectorial dado Vn sobre un campo finito GF (q) formado por q = p r elementos, donde p es un número primo y r es un entero.

Se conocen los siguientes resultados.

El número de subespacios de un espacio vectorial.

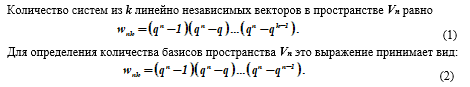
Démosle la siguiente justificación. Cada vector v1 ≠ 0 de un sistema de k vectores linealmente independientes (v1, v2,…, vk) se puede elegir de q ⁿ - 1 formas. El siguiente vector v2 ≠ 0 no se puede expresar linealmente en términos de v1, es decir se puede elegir de q ⁿ - q formas, etc.

El último vector vk ≠ 0 tampoco se expresa linealmente en términos de los vectores v1, v2,…, vk previamente seleccionados y, por lo tanto, puede elegirse de q ⁿ - q ^k - 1 formas. El número total de formas de seleccionar un conjunto de vectores v1, v2, ..., vk, por lo tanto, se define como el producto del número de selecciones de vectores individuales, lo que da la fórmula (1). Para el caso en que k = n, tenemos wp = wn, n y de la fórmula (I) obtenemos la fórmula (2).

Resultados de generalización importantes sobre las dimensiones de los subespacios.

La colección de todas las tuplas de longitud n ortogonales al subespacio V1 de tuplas de longitud n forma el subespacio V2 de tuplas de longitud n. Este subespacio V2 se denomina espacio nulo para V1.

Si un vector es ortogonal a cada uno de los vectores que generan el subespacio V1, entonces este vector pertenece al espacio cero para V1.

Un ejemplo de (V1) es el conjunto de vectores de 7 bits de la matriz generadora del código de Hamming (7,4), con un subespacio cero (V2) de vectores de 7 bits que forman la matriz de verificación de paridad de este código.

Si la dimensión del subespacio (V1) de conjuntos de longitud n es igual a k, entonces la dimensión del subespacio cero (V2) es igual an - k.

Si V2 es un subespacio de tuplas de longitud n y V1 es un espacio cero para V2, entonces (V2) es un espacio cero para V1.

Sea UV la colección de vectores que pertenecen tanto a U como a V, entonces U∩V es un subespacio.

Sea U⊕V el subespacio que consiste en la colección de todas las combinaciones lineales de la forma a u + b v , donde u є U, v є V, ab son números.

La suma de las dimensiones de los subespacios U∩V y U⊕V es igual a la suma de las dimensiones de los subespacios U y V.

Sea U2 el subespacio cero para U1 y V2 el espacio cero para V1. Entonces U2∩V2 es el espacio cero para U1⊕V1.

Conclusión

El artículo considera los conceptos básicos de los espacios vectoriales, los cuales son frecuentemente utilizados en la construcción de modelos para el análisis de sistemas de cifrado, codificación y esteganográficos, procesos que ocurren en ellos. Entonces, en el nuevo estándar de cifrado estadounidense, se utilizan espacios afines y en firmas digitales en curvas elípticas, tanto espacios afines como

proyectivos (para acelerar el procesamiento de puntos de curva).

No estamos hablando de estos espacios en la obra (no se puede agrupar todo en un montón, y también limito el volumen de publicación), pero la mención de esto no es en vano. Los autores que escriben sobre medios de protección, sobre algoritmos de cifrado, creen ingenuamente que comprenden los detalles de los fenómenos descritos, pero la comprensión de los espacios euclidianos y sus propiedades se traslada sin reservas a otros espacios, con propiedades y leyes diferentes. La audiencia lectora se engaña sobre la simplicidad y accesibilidad del material.

Se crea una imagen falsa de la realidad en el campo de la seguridad de la información y equipos especiales (tecnología y matemáticas).

En general, tomé la iniciativa, cuán afortunados son los lectores para juzgar.

Literatura

1. Avdoshin S.M., Nabebin A.A. Matemáticas discretas. Álgebra modular, criptografía, codificación. - M.: DMK Press, 2017.-352 p.

2. Akimov O.E. Matemáticas discretas Lógica, grupos, gráficas - M .: Lab. Base. Zn., 2001.-352 p.

3. Anderson D.A. Matemáticas discretas y combinatoria), Moscú: Williams, 2003, 960 p.

4. Berlekamp E. Teoría de la codificación algebraica. -M.: Mir, 1971.- 478 p.

5. Vaulin A.E. Matemáticas discretas en problemas de seguridad informática. H 1- SPb.: VKA im. A.F. Mozhaisky, 2015, 219 p.

6. Vaulin A.E. Matemáticas discretas en problemas de seguridad informática. H 2- SPb.: VKA im. A.F. Mozhaisky, 2017.-151 p.

7. Gorenstein D. Grupos simples finitos. Introducción a su clasificación.-M.: Mir, 1985.- 352 p.

7. Graham R., Knut D., Ptashnik O. Matemáticas concretas. Fundamentos de la informática.-M.: Mir, 1998.-703 p.

9. Elizarov V.P. Anillos terminales.- M .: Helios ARV, 2006. - 304 p.

Ivanov B.N. Matemáticas discretas: algoritmos y programas-M.: Lab.Baz. Conocimiento., 2001.280 p.

10. Yerusalimsky Ya.M. Matemáticas discretas: teoría, problemas, aplicaciones-M .: Vuzovskaya kniga, 2000.-280 p.

11. Korn G., Korn T. Manual de matemáticas para científicos e ingenieros.-M .: Nauka, 1973.-832 p.

12. Lidl R., Niederreiter G. Campos finitos: En 2 volúmenes, Vol. 1 -M.: Mir, 1988. - 430 p.

13. Lidl R., Niederreiter G. Campos finitos: En 2 volúmenes, Vol. 2 -M.: Mir, 1988. - 392 p.

14. Lyapin E.S., Aizenshtat A.Ya., Lesokhin M.M., Ejercicios sobre la teoría de grupos.- Moscú: Nauka, 1967.-264 p.

15. Murmura V.M. Fundamentos de la transmisión de información anti-jamming. -L. Energoatomizdat, 1990, 288 p.

16. Nabebin A.A. Matemáticas discretas.- M.: Lab. Base. Conocimiento., 2001.280 p.

17. Novikov F.A. Matemáticas discretas para programadores.- SPb.: Peter, 2000.-304 p.

18. Rosenfeld B.A. Espacios multidimensionales.-M.: Nauka, 1966.-648 p.

18. Hall M. La teoría de grupos.-M.: Izd. IL, 1962.- 468 p.

19. Shikhanovich Yu.A. Grupos, anillos, celosías. - SPb.: Kirtsideli, 2006. - 368 p.

20. Shneperman L.B. El curso de álgebra y teoría de números en problemas y ejercicios: En 2 horas Parte 2.-Mn.: Vysh. shk., 1987.-256 p.

21. Shneperman LB Colección de problemas de álgebra y teoría de números.- Minsk: Design PRO, 2000. -240 p.

Espacios vectoriales