Dos matemáticos prueban la primera etapa de la conjetura favorita de Erd sobre patrones en secuencias de números

Un par de matemáticos probaron la primera parte de una de las hipótesis más famosas sobre las propiedades aditivas de los números enteros. Fue propuesto hace más de 60 años por el legendario matemático húngaro Pal Erdos . Suena así: en qué punto de una lista infinita de números enteros hay patrones garantizados de al menos tres números espaciados a la misma distancia entre sí, por ejemplo, 26, 29 y 32.
Erdos ha formulado miles de problemas durante su carrera, pero la pregunta es: cuya lista de números contiene números que son equidistantes entre sí (lo que los matemáticos llaman progresiones aritméticas) era uno de sus favoritos. "Creo que mucha gente vio esto como la principal preocupación de Erds", dijo Timothy Gowers de la Universidad de Cambridge. Gowers, que recibióFields Prize en 1998, pasó muchas horas tratando de solucionar este problema. “Prácticamente todas las combinatorias aditivas bastante ambiciosas han intentado resolverlo”, dijo, refiriéndose a la rama de las matemáticas a la que pertenece esta hipótesis.
Por lo general, es más probable que las listas de números más densas contengan una progresión aritmética que las escasas. Por lo tanto, Erdos sugirió una simple verificación de la densidad de una lista: agregue los valores inversos de los de la lista. Si hay suficientes números para hacer que esta suma sea infinita, entonces, según Erdös, la lista debería contener un número infinito de progresiones aritméticas de cualquier longitud finita: tres, cuatro, etc. números en una fila.
En un artículo publicado en línea el 7 de julio por Thomas Bloom de Cambridge y Olaf Sisaskde la Universidad de Estocolmo demostró esta hipótesis en el caso de tripletes de números uniformemente espaciados, como 5, 7 y 9. Este par mostró que cuando la suma de recíprocos de los números en una lista es infinita, debe haber infinitos triples de números igualmente espaciados en ella.

Thomas Bloom de Cambridge
“Este es el resultado más notable en muchos años”, dijo Nets Katz del Instituto de Tecnología de California. "Este es un evento significativo".
Uno de los conjuntos, la suma de números recíprocos a los que tiende al infinito, son números primos, aquellos que son divisibles solo por 1 y ellos mismos. En la década de 1930, Johannes van der Corputusó una estructura especial de números primos para mostrar que en ellos de hecho puede encontrar un número infinito de tripletes igualmente espaciados (por ejemplo, 17, 23 y 29).
Sin embargo, el nuevo descubrimiento de Bloom y Sisask significa que no es necesario comprender profundamente la estructura única de los números primos para demostrar que hay un número infinito de triples en ellos. Basta con saber sólo que hay suficientes números primos para que la suma de sus valores recíprocos sea infinita, y esto lo saben los matemáticos desde hace muchos siglos. “El resultado de Thomas y Olaf nos dice que incluso si su estructura fuera completamente diferente a la que realmente tienen, el mero hecho de tener una gran cantidad de ellos garantizaría infinidad de progresiones aritméticas”, nos escribió Tom Sanders .de la Universidad de Oxford.
El nuevo trabajo tiene 77 páginas y los matemáticos necesitarán algo de tiempo para verificarlo a fondo. Sin embargo, muchos se muestran optimistas al respecto. “Realmente parece que la prueba de esta afirmación debería verse así”, dijo Katz, cuyo trabajo inicial formó la base para esto.
El teorema de Bloom y Sisask dice que si la lista de números es lo suficientemente densa, deben aparecer ciertos patrones en ella. Este descubrimiento es consistente con el lema fundamental de las matemáticas, como lo llama Sarah Pillus de Oxford, formulado por primera vez por Theodore Motzkin: "No hay desorden absoluto".
Densidad disfrazada
Es bastante fácil crear una lista infinita sin progresiones aritméticas si la hace lo suficientemente escasa. Por ejemplo, considere la secuencia 1, 10, 100, 1,000, 10,000, ... Los recíprocos suman 1.111 (1). La distancia entre estos números crece tan rápidamente que no se puede encontrar ni un solo triplete de números ubicados a la misma distancia entre sí.
Sin embargo, es posible que se pregunte si existe una lista más densa de números que todavía no tiene progresiones aritméticas. Puede, por ejemplo, caminar a lo largo de la recta numérica y dejar cada número que no esté incluido en las progresiones aritméticas. Obtenemos la secuencia 1, 2, 4, 5, 10, 11, 13, 14, ... que a primera vista parece bastante densa. Sin embargo, con el tiempo, se vuelve cada vez más escaso; por ejemplo, cuando llegamos a números de 20 dígitos, tomaremos solo el 0.000009% de todos los números enteros de la recta numérica. En 1946, a Felix Berend se le ocurrieron ejemplos más densos, pero también se vuelven escasos muy rápidamente: el conjunto de Berend, que alcanza números de 20 dígitos, contiene solo el 0,001% de todos los números enteros.
Por otro lado, si su conjunto contiene casi todos los números enteros, definitivamente contendrá secuencias aritméticas. Pero entre estos dos extremos se encuentra un vasto territorio medio, casi sin marcar. ¿Qué tan escaso puede ser un conjunto, especulaban los matemáticos, de modo que las progresiones aritméticas todavía pudieran garantizarse allí?

Olaf Sisask de la Universidad de Estocolmo
Erdos (como dicen, posiblemente junto con el matemático húngaro Pal Turan) dio una posible respuesta. Su condición para la suma de recíprocos es la densidad enmascarada. Resulta que esto es lo mismo que decir que la densidad de una lista hasta el número N no es menor que uno dividido por el número de dígitos en N. En otras palabras, su lista puede volverse cada vez más escasa a medida que avanza a lo largo de la recta numérica, pero solo si sucede muy lentamente. En números de 5 dígitos, la densidad de su lista debe ser de al menos 1/5; en 20 dígitos, al menos 1/20, y así sucesivamente. Y si se cumple esta condición, entonces, como sugirió Erdos, su lista debe contener un número infinito de progresiones aritméticas de cualquier longitud.
En 1953, Klaus Roth puso a los matemáticos en el camino que conduce a la demostración de la conjetura de Erds. En un artículo que le valió un premio Fields ese año, definió una función de densidad que garantiza tripletes equidistantes de números. La densidad no era tan baja como la de Erds, pero sin embargo se acercó a cero a medida que avanzábamos por la recta numérica. El teorema de Roth significaba que en la lista de números cuya densidad finalmente cae por debajo del 1%, y luego por debajo del 0,1%, y luego por debajo del 0,01%, y así sucesivamente, debe haber progresiones aritméticas, si solo su densidad cae lo suficiente. lento.

Conferencia de Pal Erd "60 años en matemáticas" en la Universidad de Cambridge en junio de 1991.
En primer lugar, el enfoque de Roth se basó en el hecho de que la mayoría de las listas con la densidad que él eligió "quieren" tener progresiones aritméticas; tienen suficientes pares de números diferentes, de modo que es casi seguro que algunos de los puntos medios entre estos pares también aparezcan en esta lista, lo que conduciría a la aparición de trillizos igualmente espaciados. El truco es cómo pasar de una lista de "casi todos" los números a una lista de "todos" los números, aunque la estructura completa podría diseñarse especialmente para evitar progresiones aritméticas.
Habiendo recibido tal lista, Roth descubrió cómo "destilar" su estructura marcando su "espectro de frecuencia" usando la transformada de Fourier.... Muestra cuáles de los patrones emergentes son más pronunciados: las mismas matemáticas subyacen en tecnologías como la cristalografía de rayos X y la radioespectroscopía.
Algunas frecuencias parecen más fuertes que otras y estas variaciones enfatizan los patrones existentes; por ejemplo, la frecuencia puede indicar que la lista contiene más números impares que pares. Si es así, puede concentrarse solo en números impares y obtener una lista más densa en comparación con una lista de solo números impares. Roth pudo demostrar que después de varias de estas destilaciones, una lista sería tan densa que las progresiones aritméticas tendrían que estar presentes en ella.
El enfoque de Roth ha inspirado muchos artículos en teoría analítica de números durante los últimos cincuenta años, dice Jacob Fox de la Universidad de Stanford. "Sus ideas fueron muy influyentes".
Juego, set, partido
Sin embargo, el método de Roth funcionó solo para aquellos conjuntos de números que ya eran bastante densos desde el principio; de lo contrario, las destilaciones constantes simplemente evaporarían todos los números. Otros matemáticos encontraron constantemente formas de utilizar este método de manera cada vez más eficaz, pero no pudieron acercarse a la densidad descrita en la hipótesis de Erds. "Este obstáculo parecía muy difícil", dijo Fox.
Luego, en 2011, Katz y Michael Bateman descubrieron cómo superar este obstáculo en términos más simples: en el juego de cartas Seth, donde los jugadores buscan conjuntos de tres cartas marcadas con diferentes símbolos. El juego Tres del conjunto se puede definir como una progresión aritmética y, como en el caso de una lista de números enteros, puede preguntarse qué fracción de todas las cartas necesita poner sobre la mesa para encontrar seguramente al menos un tres.
Colección de juegos"
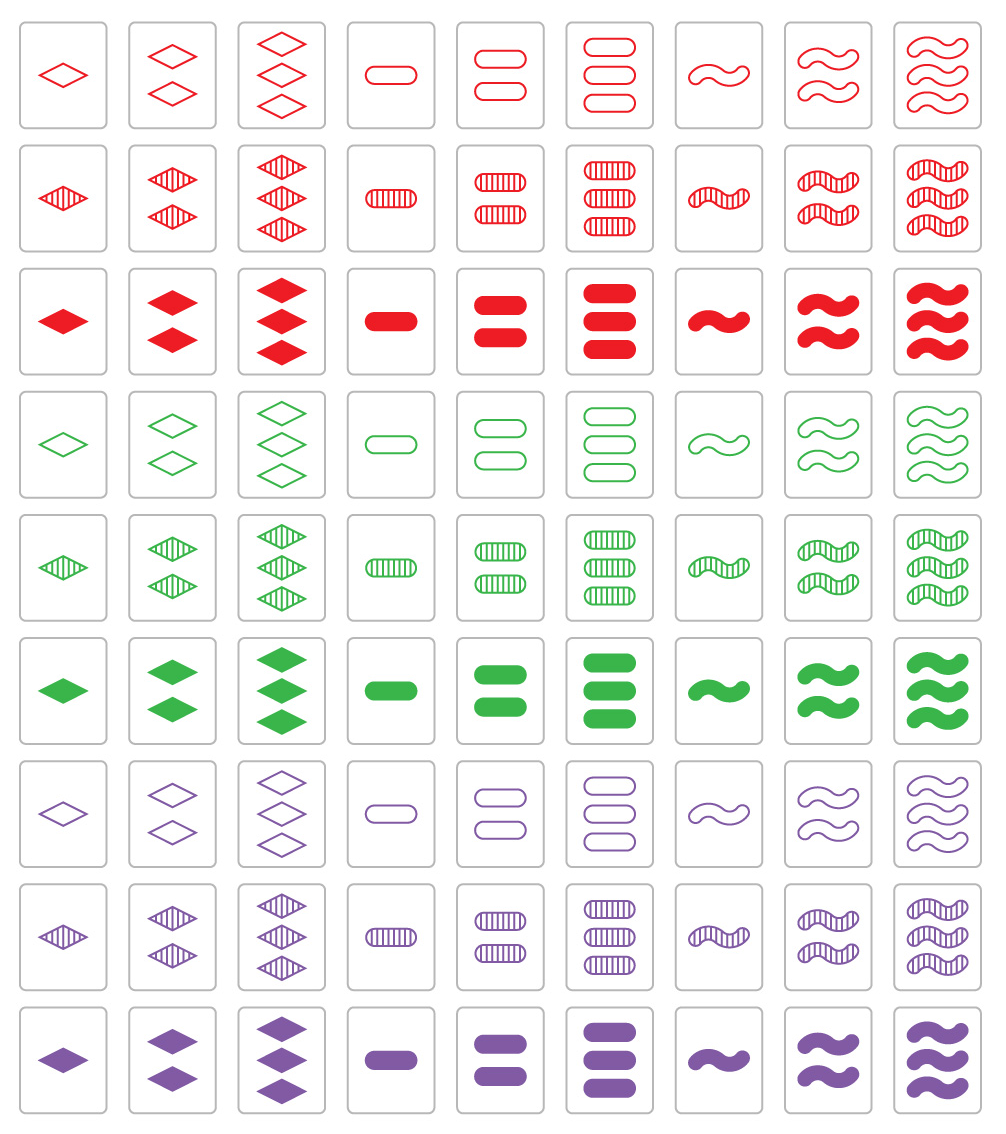
El objetivo del juego es encontrar tripletes especiales de cartas, o "conjuntos", en una baraja de 81 cartas. Cada tarjeta tiene su propio dibujo con cuatro propiedades: color (rojo, violeta, verde), forma (óvalo, rombo, onda), sombreado (contorno, rayas, completamente rellenado) y el número de formas (una, dos o tres). En el juego normal, se reparten 12 cartas boca arriba en la mesa y los jugadores buscan conjuntos de tres cartas en las que cada uno de los cuatro atributos sea el mismo para todas las cartas o diferente para todas las cartas. Si no hay juegos de este tipo entre las 12 cartas, se añaden más cartas.
Cubierta entera
, –
| ? |  |
 |
 |
 |
Una manera fácil de recolectar un juego de cartas lo suficientemente grande sin tripletes es tomar solo cartas que tengan solo dos o tres opciones para cada atributo. El tamaño de esta colección será (2/3) n de todo el mazo, donde n es el número de atributos.

Esta pregunta (relacionada no solo con el conjunto de juegos estándar, sino también con sus variantes más grandes) es un modelo natural para estudiar la pregunta correspondiente con respecto a los números enteros. Por lo tanto, los matemáticos esperaban que el avance de Bateman y Katz pudiera abrir el camino para probar la conjetura de Erd, especialmente cuando se combina con otros avances recientes . Poco después del lanzamiento del trabajo de Bateman y Katz, Gowers lanzó el " proyecto de políma"- una colaboración masiva fue diseñado para hacer el intento.
Sin embargo, el proyecto se detuvo rápidamente" En ella se reunieron una gran cantidad de argumentos técnicos, - dijo Gowers -. Este proyecto es más adecuado para una o dos personas, durante mucho tiempo y trabajando lentamente en ella.".
Por Afortunadamente, un par de matemáticos se estaban preparando para esto. Bloom y Sisask, al principio por separado, ya comenzaron a reflexionar sobre la hipótesis de Erd, cautivados por la belleza de las técnicas utilizadas en ella. "Este fue uno de los primeros problemas de investigación que enfrenté", dijo Sisask. , quien, como Bloom, tiene ahora unos 35 años.
Bloom y Sisask unieron fuerzas en 2014 y en 2016 decidieron que estaban cerca de una solución. Bloom incluso anunció esto en su conferencia, y solo después de eso descubrió que algunas de las soluciones que encontraron resultaron ser incorrectas. La pareja continuó trabajando, sumergiéndose en el método de Bateman y Katz, y finalmente se dieron cuenta de qué nuevas ideas les permitirían transferir este método del mundo de Seth al mundo de los enteros.
El nuevo trabajo parece ser correcto desde todos los ángulos, dijo Katz. "No creí sus declaraciones anteriores, pero sí creo esto".
El trabajo de Bloom y Sisask es "un logro tremendo", dijo Fox. Ellos y otros matemáticos están ansiosos por saber si las técnicas del nuevo trabajo se aplican a otros problemas. "Creo que estos métodos tendrán un gran impacto en las matemáticas", dijo Fox.
En cuanto a la hipótesis de Erdos en su totalidad, el trabajo en ella aún está lejos de estar completo. Bloom y Sisask probaron esta hipótesis solo para tripletes de números igualmente espaciados, pero no para progresiones aritméticas más largas; esta tarea aún está fuera de alcance.
E incluso la cuestión de los tres, que Bloom y Sisask ya han cerrado, en opinión de muchos matemáticos, no ayuda especialmente. Tan difícil como es probar que la densidad de Erd garantiza tripletes equidistantes de números, los matemáticos sospechan que la densidad real a la que esta garantía deja de funcionar es mucho menor, quizás un poco más alta que la densidad de los conjuntos que diseñó Berend.
"Esto no quiere decir que hayamos resuelto completamente este problema", dijo Bloom. "Arrojamos un poco más de luz sobre ella".
Bloom y Sisask probablemente hayan exprimido lo mejor de los métodos actuales, dijo Fox. “Debería haber algunas herramientas completamente nuevas que nos permitan avanzar mucho más y obtener un resultado dramáticamente mejor”, dijo. Sin embargo, "probablemente este no sea el final de la historia".