
La interacción de información de los suscriptores en redes informáticas y de comunicación está sujeta a perturbaciones que conducen a errores y perturbaciones de diversa índole. Además de los errores en los mensajes transmitidos, es posible el acceso no autorizado al contenido de los mensajes del infractor. La lucha contra estos fenómenos indeseables se lleva a cabo durante milenios, pero con éxito variable. Los creadores de Internet no lo concibieron en absoluto como es ahora. Entonces ni siquiera pensaban en los piratas informáticos.
Los principales problemas teóricos de la confrontación de información, las tareas para resolverlos se asignan a las teorías de la codología, criptología y esteganología, en las que las direcciones del codoanálisis, criptoanálisis y esteganálisis se desarrollan intensamente en todo el mundo. Los aspectos prácticos tampoco se quedan al margen, pero señalaré que en la Federación de Rusia la actividad no es muy alta, la inercia de los jóvenes afecta (yo mismo ya he cambiado la novena década, pero la administración Habr limitó el límite de edad en 1950). Mi opinión, por supuesto, se limita a la observación de la descendencia (hasta bisnietos) y la comunicación en Internet, así como con los aprendices y empleados de la empresa en la que trabajo a tiempo parcial. Los medios también agregan negatividad. Algunos de los jóvenes se han vuelto un poco más sabios, ve a la colina. Puedes ver el comportamiento de los demás tú mismo.
Visita guiada de publicaciones
El desarrollo (síntesis) de dispositivos técnicos requiere del desarrollador ciertos conocimientos, la capacidad de utilizarlos y otras habilidades de este tipo. Un componente esencial de tal conocimiento son las matemáticas. Estos son, por regla general, álgebra, matemáticas discretas, geometría, física, lógica matemática, etc. Aquí en el artículo consideraremos las estructuras algebraicas no del todo en la presentación clásica, pero con un nivel suficiente de rigor y precisión. Mi tarea principal es asegurar la accesibilidad y claridad de la presentación de las cosas que utilizo en mis textos e investigaciones.
Por ejemplo, aquí se utiliza el campo de extensión GF (2 8) y, si prescindimos de él, no se puede afirmar nada que valga la pena. Mis criterios de evaluación son sencillos. Cada semestre 2, o incluso 3 exámenes y pruebas en diferentes grupos de estudio. Allí escucho y veo lo que expuse, lo llevé a la práctica y lo que se me devuelve en las respuestas de los boletos de examen. El análisis de las respuestas de los exámenes es muy útil, veo que algo debería haberse dicho de otra manera, mejor.
Y aquí las propiedades Z Nde un anillo de residuo numérico finito módulo N = pq se utilizan para encontrar una solución al problema de factorizar números grandes dentro del marco de un nuevo enfoque original. Está claro que en cada una de las publicaciones posteriores no sería razonable transferir parte de las herramientas matemáticas estándar, por lo que se decidió recopilar todo en un solo lugar y, si es necesario, dirigirse a los lectores aquí.
Aquí se considera y utiliza un grupo de puntos de una curva elíptica en un plano. La operación de suma en un grupo es de un tipo muy especial, provocando preguntas desconcertantes, como cómo se las arregla para sumar los puntos de la curva, incluso de los miembros del HEC.
Grupos
Primero presentamos una serie de definiciones necesarias.
Definición . Conjunto finito A -conjunto, colección de cualquier n objetosenumerados en cualquier orden pero no duplicados. Los conjuntos pueden estar estructurados, sobre cuyos elementos se especifican una (o más) operaciones y relaciones, y no estructurados, cuando no se especifican operaciones.
A continuación, como recordatorio, se proporciona una tabla de acciones (operaciones) con conjuntos discretos finitos y, para mayor claridad, los diagramas también muestran conjuntos continuos A y B.
Tabla de operaciones con conjuntos
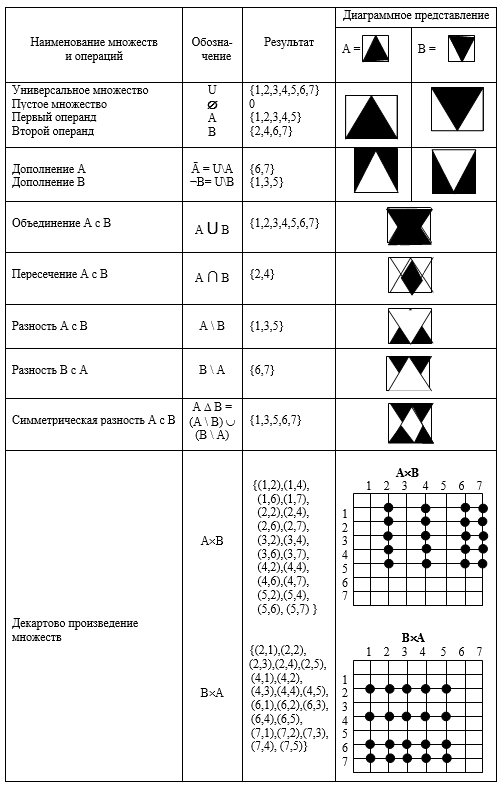
Definición . Una operación es un mapeo A × A → A o, por ejemplo, a · b = c; a, b, c ∊ A. Se consideran operaciones en estructuras algebraicas distintas de la aritmética: unaria (por ejemplo, inversión b -1 ), binaria, ternaria, ..., n-aria (según el número de lugares para los operandos) o multiplicación permutaciones, modular (tomando el resultado por (mod R)), etc. Se dice que los elementos ayb permutan o conmutan si ab = ba.
Definición . Un grupo es un conjunto de elementos G (de cualquier naturaleza) sobre los cuales se especifica una sola operación, pero puede ser suma (+) y el grupo se llama aditivo , su elemento neutro (0) o multiplicación (◦) se llama multiplicativo, su elemento neutral (1), pero como regla, estas operaciones no son aritméticas ordinarias, sino especiales. El grupo a menudo se denota con el símbolo (G, ◦); entre todos los grupos, se da un lugar importante a los grupos simétricospermutaciones de grado n. Las partes de los elementos de un grupo que conservan las propiedades de un grupo se denominan subgrupos. En esencia, estos son los mismos grupos, solo que más pequeños que el original. Esta es una definición informal de un grupo, la formal se dará un poco más tarde.
El grupo G, que satisface la ley conmutativa ba = ab para todo a, b ε G recibe el nombre del matemático Abel (1802-1829) Abeliano .
Un ejemplo de un grupo aditivo es el conjunto de palabras del código Hamming ( ver aquí). La operación en este grupo es de orden 16: suma de palabras por (mod2). Con este grupo se realizó la operación de descomposición en clases contiguas de un grupo de 128 palabras por el subgrupo del código, y también se construyó la tabla Keli, los elementos del grupo se utilizan en el codificador (base del espacio de dimensión 4) y el decodificador. En una palabra, este ejemplo demuestra claramente cómo se puede utilizar incluso un grupo pequeño para resolver un problema práctico muy importante (comunicación).
Los grupos de permutación simétrica (permutación) son muy importantes en la teoría de grupos. Esta importancia está determinada por el teorema, que dice que para cualquier grupo que surja en un área temática arbitraria, existe un grupo simétrico (subgrupo) isomorfo en las permutaciones. Entonces la tarea de estudiarlo se simplifica para el investigador de un nuevo grupo abierto. Casi todas las propiedades del grupo de permutación isomórfica son válidas en el nuevo grupo.
Comencemos con un ejemplo sencillo. Se dan N elementos (los denotamos con los números 1, 2, 3, ..., n) y formamos permutaciones a partir de ellos, ¡el número de los cuales es n! = 1 2 3 ... n. ¡Limitémonos al valor n = 3, luego 3! = 6.
Definición . Orden de grupo : el número de elementos de un grupo se denomina orden. En el ejemplo, el número 6 es el orden del grupo.
En un grupo, cada elemento también tiene un orden que es un divisor del orden del grupo.
Definición . El orden de un elemento de un grupo es el exponente más pequeño de un elemento en un grupo multiplicativo (multiplicidad en el aditivo b + b + b + b + ... b = nb = 0, order = n) en el que se convierte en un elemento neutro, por ejemplo () 3 = 1, orden ord () = 3.
En el grupo simétricola operación es la multiplicación de permutaciones. Esta multiplicación es similar a la multiplicación de matrices, ya que cada permutación de grado n está asociada con una matriz de permutación cuadrada n × n en la que cada fila y columna contiene una sola unidad. Esto se muestra a continuación para el grupo simétrico...

Para la conveniencia de trabajar con un grupo y sus elementos, el matemático Keli propuso una tabla de operaciones grupales (de tamaño limitado). En la celda de la intersección de una fila y una columna se pone el resultado de la operación con los elementos que las denotan. El resultado (así como la designación de filas / columnas) en la tabla está representado por números de elementos decimales, lo que ahorra espacio.
Tabla de multiplicar de elementos (permutaciones) de un grupo

Completar 36 celdas de la tabla de multiplicar se simplifica usando las propiedades de la tabla de Keli.
- Todas las filas y columnas contienen elementos de todo el grupo.
- Las columnas extremas están ordenadas lexicográficamente y dirigidas de manera opuesta (1 ° arriba / abajo - el último es viceversa)
- En la diagonal principal de la tabla hay cuadrados de elementos, si hay 1, entonces el elemento correspondiente es involución; involuciones enson
- Con respecto a las diagonales de la matriz, se realiza la simetría de las posiciones de los elementos.
Las propiedades de la tabla permiten, al llenarla, restringir los cálculos a solo 13 pares de elementos (se muestran arriba).
Grupo simétrico
Grupo tiene un pedido pequeño (6) y no es muy conveniente para ilustrar propiedades. A continuación daremos ejemplos con el grupo simétrico24 pedidos. Todas las permutaciones pares de grado n forman un subgrupo alterno en el grupo simétrico, denotado por el símbolo A n .
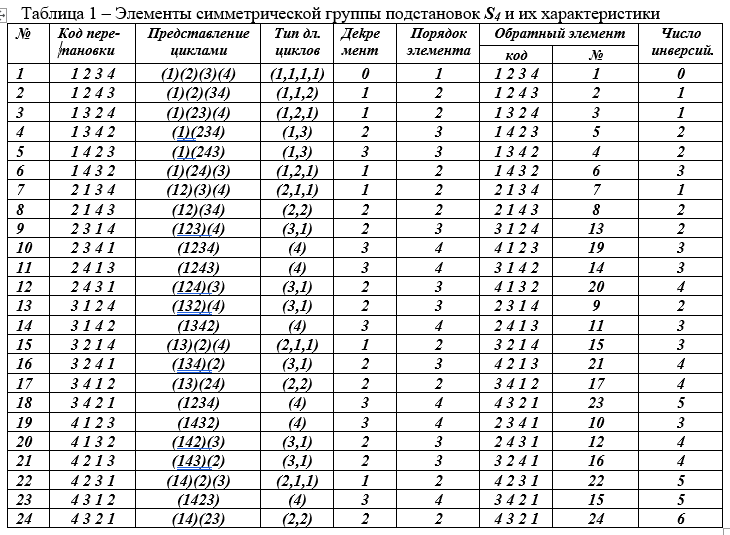
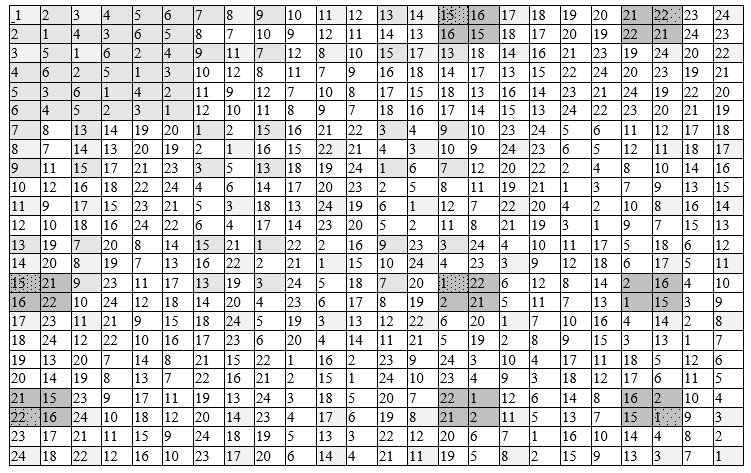
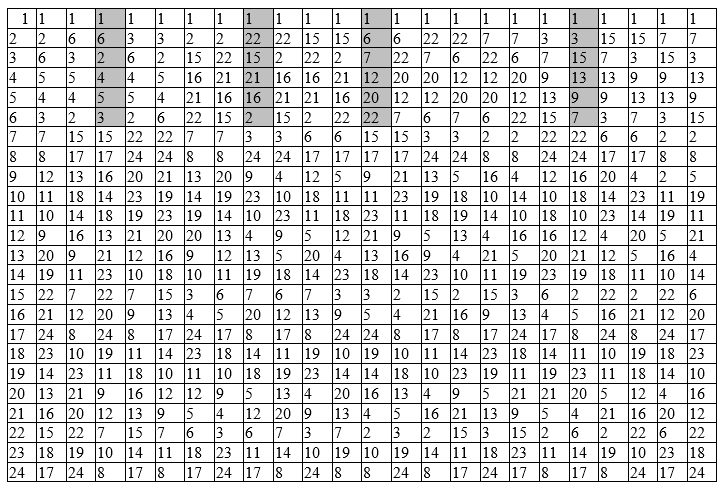
La tabla 2 se puede utilizar para encontrar los productos de cualquier par de elementos.o para toda su cadena, pero se encuentran mediante la multiplicación secuencial del resultado por el siguiente elemento. No puede reorganizar los elementos en el trabajo. La operación de multiplicar permutaciones no es conmutativa, como lo es la multiplicación de matrices. Un elemento, cuando se multiplica por sí mismo muchas veces hasta obtener 1, forma un grupo cíclico de todos los resultados intermedios. El orden de dicho subgrupo cíclico es el orden del generador, debe dividir el orden del grupo grande original.
Según la tabla de multiplicar, hay subgrupos dentro de un grupo grande. Recuerde que el orden del subgrupo más pequeño debe dividir el orden del más grande.
Construimos un grupo cíclico con el elemento p 14 generador . Entramos en la tabla 2. En la línea 14 encontramos en la intersección con p 14elemento de columna p 24 ; en la línea 24 encontramos el elemento p 11 en la celda de intersección con la columna 14, y finalmente en la celda de la fila 11 en la intersección con la columna 14 encontramos el elemento p 1 , es decir elemento neutro 1. Entonces, p 14 · p 14 · p 14 · p 14 = p 1 , estos son elementos del subgrupo de 4to orden, cuyo valor divide completamente el orden 24: 4 = 6. Para ello, se puede construir la tabla de Keli y no contiene no aparecerán elementos distintos a los encontrados En este subgrupo, los elementos p 14 y p 11 tienen el 4º orden y p 24 el segundo es una involución.
Morfismos de grupo
Un mapeo f de un grupo (G, *) a un grupo (G ', ◦) se llama homomorfo (u homomorfismo) si, para cualquier a, b ∊ G, f (a * b) = f (a) ◦f (b). Por lo general, estas igualdad continúan como f (e) = e ',
f (a -1 ) = (f (a)) -1 . La notación a la derecha de la igualdad denota la imagen y se llama imagen; a la izquierda, la preimagen del mapeo f. En el caso general, las operaciones sobre la imagen y la preimagen no coinciden. La imagen inversa de la identidad (G ', ◦) bajo el homomorfismo f se denomina núcleo de este homomorfismo y se denota con ker f. Un ejemplo bien conocido de los años escolares es un
registro de mapeo (a◦b) = log (a) + log (b).
Elementos de la imagen con una operación sobre ellos (+), y en la preimagen los elementos están conectados por la operación (◦) de multiplicación. Una imagen homomórfica de un grupo es un grupo (subgrupo), es decir, si un f-homomorfismo de G sobre G 'y G es un grupo, entonces G' también es un grupo. Un homomorfismo es una generalización del isomorfismo de grupo: si f es un mapeo homomórfico uno a uno de G sobre G ', entonces es isomorfo, que se denota como G≈G'.
Dos grupos G y G 'con operaciones (·) y (*) se denominan isomorfos si existe un mapeo f: G → G' tal que (el mapeo f conserva la operación de grupo) de la imagen;
Teorema. Sea H un subgrupo normal de un grupo G y G = G / H. Entonces el mapeo f del grupo G sobre G dado por la fórmula f (a) = aes un homomorfismo. El núcleo de este homomorfismo es H. Este homomorfismo a menudo se denomina natural (canónico).
Los homomorfismos de grupo se agotan esencialmente mediante homomorfismos canónicos.
Descompongamos el grupo G de orden 24 con respecto a su subgrupo H = {1,8, 17,24} en clases laterales y construyamos para esta descomposición un grupo cociente con respecto al subgrupo H. Para ello, escribimos en columnas los productos izquierdo y derecho de los elementos del subgrupo H.
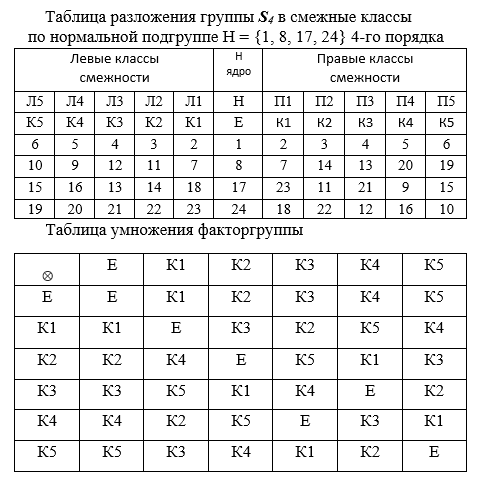
En la tabla de descomposición de un grupo G de orden 24 en clases laterales con respecto al subgrupo H, las columnas l1, l2, l3, l4, l5 se designan con los nombres de las clases laterales izquierda y n1, n2, n3, n4, n5 - las clases laterales derecha, los principales representantes de las clases, uno por columna, están escritos en línea siguiente.
La columna del medio H es un grupo de cuarto orden (el núcleo del homomorfismo). Las columnas se llenan con los productos de los principales representantes de las clases y los elementos del grupo H. Después de completar las columnas, se comparan las clases. Si las composiciones de las clases izquierda y derecha coinciden, entonces simplemente hablan de clases laterales y denotan H = K0, K1, K2, K3, K4, K5. Además, el subgrupo H se denomina normal . Al completar la tabla, el representante principal de la siguiente clase selecciona el elemento G más pequeño de los que no están incluidos en las clases ya construidas.
Las clases laterales resultantes se consideran a continuación como elementos de un nuevo grupo denominado grupo cociente del grupo G por el subgrupo H ( se indica el grupo cociente G = G / H). La operación en este nuevo grupo es la multiplicación de clases: para cada par de clases, por ejemplo, K3 × K5 = K2, se construye una tabla de 4 × 4, en la que las filas están marcadas con los elementos del primer factor, y las columnas, el segundo. Además, la multiplicación se realiza como en el grupo G. El resultado de dicha multiplicación da 16 elementos, pero todos pertenecen a la misma clase, en nuestro caso la clase K2.
Además de las asignaciones de isomorfismos, los homomorfismos son endomorfismos y automorfismos. Un homomorfismo de un grupo G en sí mismo se llama endomorfismo, y un isomorfismo de un grupo G en sí mismo es un automorfismo. Estos conceptos son comparables a los conceptos de mapas de conjuntos no estructurados por inyección, sobreyección y biyección.
Tabla 2 - Grupo simétrico Keli$ en línea $


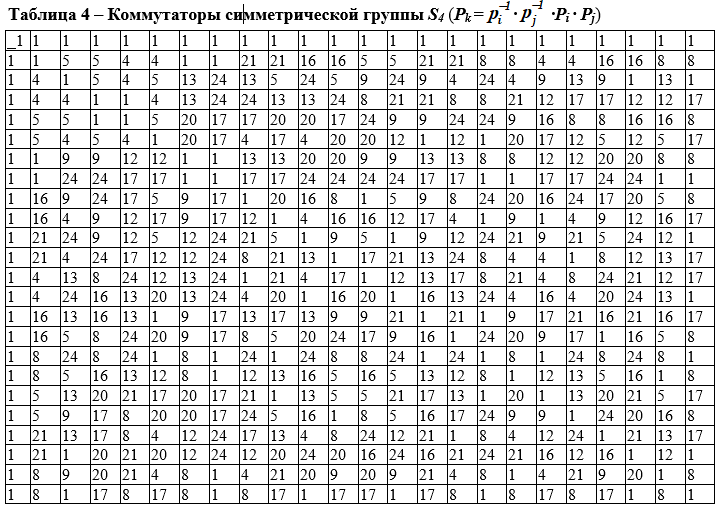
Conmutador
A cada par de elementos a, b ∊ G asociamos un elemento llamado conmutador de este par
[a, b] = a -1 b -1 ab. El subgrupo K de un grupo G generado por todos sus conmutadores se denomina subgrupo de conmutadores del grupo G o un subgrupo derivado.
Un grupo G se llama solucionable si la cadena G ⊇ G '⊇ G' '⊇… ⊇ G (i) ⊇ ..., donde cada subgrupo G (i) es un subgrupo de conmutadores del anterior, termina después de un número finito de pasos en el subgrupo de unidades, por ejemplo, G (f) = 1.
En la Tabla 4, el subgrupo alterno G '= A 4 de orden 12 es normal, de G = de orden 24, ya que las clases laterales izquierda y derecha de este subgrupo coinciden (las clases son el mismo complemento del grupo completo ). Luego, la tabla 4 se contrae en una tabla más pequeña de 4 × 4 (conmutador) que contiene los elementos G '' = {1,8,17,24} de un nuevo subgrupo cuyo conmutador es 1. La tabla 4 ilustra la capacidad de solución del grupo...
Conclusión
El artículo analiza algunas de las principales disposiciones de la teoría de grupos, que a menudo se utilizan en publicaciones de naturaleza técnica (no teórica ni matemática). La comprensión del texto de tales publicaciones está determinada en gran medida por la posesión de herramientas matemáticas.
Para un grupo, se dan un ejemplo y una técnica de su mapeo homomórfico en un grupo cociente.
Los ejemplos numéricos pretenden servir para asegurar la disponibilidad del material presentado y en gran medida ayudar a su comprensión y asimilación, con un análisis cuidadoso o incluso repetición con lápiz en mano. Que simplemente falta en los manuales clásicos. Esto a menudo se atribuye al ahorro de espacio y tiempo.
Estoy esperando la reacción de los lectores, que dejará claro si seguir con este estilo o no.
Literatura
Avdoshin S.M., Nabebin A.A. Matemáticas discretas. Álgebra modular, criptografía, codificación. - M.: DMK Press, 2017.-352 p.
Akimov O.E. Matemáticas discretas Lógica, grupos, gráficas - M .: Lab. Base. Zn., 2001.-352 p.
Anderson D.A. Matemáticas discretas y combinatoria), Moscú: Williams, 2003, 960 p.
Berlekamp E. Teoría de la codificación algebraica. -M.: Mir, 1971.- 478 p.
Vaulin A.E. Matemáticas discretas en problemas de seguridad informática. H 1- SPb.: VKA im. A.F. Mozhaisky, 2015, 219 p.
Vaulin A.E. Matemáticas discretas en problemas de seguridad informática. H 2- SPb.: VKA im. A.F. Mozhaisky, 2017.-151 p.
D. Gorenstein, Grupos simples finitos. Introducción a su clasificación.-M.: Mir, 1985.- 352 p.
Graham R., Knut D., Ptashnik O. Matemáticas concretas. Fundamentos de la informática.-M.: Mir, 1998.-703 p.
Elizarov V.P. Anillos finales. - M.: Helios ARV, 2006. - 304 p.
Ivanov B.N. Matemáticas discretas: algoritmos y programas - M.: Lab. Base. Conocimiento., 2001.280 p.
Yerusalimsky Y. M. Matemáticas discretas: teoría, problemas, aplicaciones - M.: Vuzovskaya kniga, 2000. -280 p.
Lidl R., Niederreiter G. Campos finitos: En 2 volúmenes Vol. 1 -M .: Mir, 1988. - 430 p.
Lidl R., Niederreiter G. Campos finitos: En 2 volúmenes Vol. 2 -M .: Mir, 1988. - 392 p.
Lyapin E.S., Aizenshtat A.Ya., Lesokhin M.M., Ejercicios sobre la teoría de grupos.- Moscú: Nauka, 1967.-264 p.
Murmura V.M. Fundamentos de la transmisión de información anti-jamming. -L. Energoatomizdat, 1990, 288 p.
A.A. Nabebin, Matemáticas discretas, Moscú: Lab. Conocimiento., 2001.280 p.
F.A. Novikov Matemáticas discretas para programadores.- SPb.: Peter, 2000.-304 p.
Hall M. Teoría de grupos.-M.: Izd. IL, 1962.- 468 p.
Shikhanovich Yu.A. Grupos, anillos, celosías. - SPb.: Kirtsideli, 2006. - 368 p.
Shneperman L.B. El curso de álgebra y teoría de números en problemas y ejercicios: En 2 horas Parte 2.-Mn.: Vysh. shk., 1987.-256 p.
Shneperman L.B. Colección de problemas de álgebra y teoría de números.- Minsk: Design PRO, 2000. -240 p.