Funciones de ventana de bricolaje

En el procesamiento de señales digitales, las funciones de ventana se utilizan ampliamente para limitar la señal en el tiempo, y sus nombres son bien conocidos por todos los que se han encontrado con la transformada discreta de Fourier de una forma u otra: Hann, Hamming, Blackman, Harris y otros. Pero, ¿son suficientes, es posible inventar algo nuevo y tiene algún sentido?



En este artículo, veremos la salida de una función de ventana con nuevas propiedades usando Wolfram Mathematica. También se supone que el lector tiene un conocimiento general del procesamiento de señales digitales en el contexto del tema en discusión y que al menos está familiarizado con el artículo de Wikipedia .

Introducción

Históricamente, las primeras funciones de ventana aparecieron en el proceso de intentos de mejorar sus propiedades espectrales reduciendo la amplitud de los lóbulos laterales, ya que cuando la señal se multiplica por la función de ventana, sus espectros son intrincados, lo que introduce algunas limitaciones para el análisis. En ese momento, los años 50 del siglo XX, la potencia informática no permitía manipular de forma fácil y natural los cálculos simbólicos, y la selección de los parámetros óptimos era bastante difícil. Esta es una de las razones por las que las funciones reciben diferentes nombres: ellas, o mejor dicho, sus propiedades espectrales, han sido estudiadas por diferentes investigadores durante bastante tiempo. Un efecto secundario de esto es que el conjunto existente de funciones de ventana nombradas se percibe como una especie de "conjunto estándar" fuera del cual no se puede encontrar nada;al mismo tiempo, los nombres de estas ventanas no contienen información sobre las propiedades y sugieren su estudio y memorización por separado.

Clasificación

Todas las funciones de ventana se obtienen multiplicando alguna función por una rectangular, lo que garantiza su limitación de tiempo. Por tanto, en primer lugar, se pueden clasificar según las funciones que utilicen:

1. la suma de los cosenos. La clase más extensa debido al hecho de que su espectro es fácilmente computable y es la suma de funciones sinc ponderadas. Esto incluye a Hann, Hamming, Blackman, Harris ...
2. polinomio continuo por partes. Se obtienen como resultado de la convolución de funciones simples, por ejemplo, rectangular y triangular. Al mismo tiempo, sus espectros se multiplican y su hallazgo tampoco es particularmente difícil. Estos incluyen Dirichlet, Triangular, Parzen, Welch ...
3. todos los demás, utilizando exponenciales, gaussianos, sinc y otros, la elección de funciones específicas en las que es más de carácter ideológico que propiedades específicamente espectrales.

También se pueden dividir por propiedades en los bordes:

1. sin espacios en los bordes - valores iguales a cero. Los descansos son de Dirichlet, Hamming, Blackman-Harris. No tengo - Triangular, Hann, Nuttal
2. ausencia de discontinuidades de la 1a y otras derivadas

Dos funciones de ventana más se destacan por separado:

1. Kaiser, que le permite establecer el ancho del pétalo principal;
2. Dolph-Chebyshev, cuyos lóbulos laterales son iguales a una amplitud dada.

Ambos tienen discontinuidades en los bordes tanto de los valores como de las derivadas, y sus cálculos implican algunas dificultades: la función de Kaiser se calcula mediante una función especial (Bessel), y la función Dolph-Chebyshev se determina en el dominio de la frecuencia y se calcula mediante la transformada discreta inversa de Fourier. Encontrar sus antiderivadas analíticas también es particularmente difícil.

Ingeniería inversa

Veamos las definiciones de las funciones de Blackman y Nuttel:

BlackmanWindow[x] // FunctionExpand

↓

$$

$$\left\{ \begin{array}{ll} \frac{1}{50} (25 \cos (2 \pi x)+4 \cos (4 \pi x)+21) & -\frac{1}{2}\leq x\leq \frac{1}{2} \\ 0 & \left| x\right| >\frac{1}{2} \\ \end{array} \right.$$

NuttallWindow[x] // FunctionExpand

↓

$$

$$\left\{ \begin{array}{ll} \frac{121849 \cos (2 \pi x)+36058 \cos (4 \pi x)+3151 \cos (6 \pi x)+88942}{250000} & -\frac{1}{2}\leq x\leq \frac{1}{2} \\ 0 & \left| x\right| >\frac{1}{2} \\ \end{array} \right.$$

Son sumas de ondas coseno 3 y 4 con frecuencias pares (comenzando desde cero) y algunos coeficientes. ¿De dónde proceden estos coeficientes? Es poco probable que hayan sido seleccionados a mano, al menos cada uno por separado; después de todo, hay condiciones de contorno que las ventanas deben cumplir independientemente de sus propiedades espectrales, al menos iguales a la unidad en el centro.



Intentemos "inventar" la función Blackman por nuestra cuenta. Para hacer esto, definimos una función con coeficientes aún desconocidos

f = Function[x, a + b Cos[2 Pi x] + c Cos[4 Pi x]];

y componga un sistema de ecuaciones que definan las condiciones de contorno: igualdad a la unidad en el centro, cero en los bordes e igualdad a cero de las derivadas en los bordes:

ss = Solve[{
   f[0] == 1,
   f[1/2] == 0,
   f'[1/2] == 0
   }, {a, b, c}]

↓

$$

$$\left\{\left\{b\to \frac{1}{2},c\to \frac{1}{2}-a\right\}\right\}$$

Se encontró la solución, pero no una, sino muchas, dependiendo del coeficiente a , sobre el cual Wolfram nos advirtió cortésmente. Ahora, a partir de la solución encontrada, definimos una nueva función en función del coeficiente desconocido: ↓ Es fácil ver que para a = 0,42 obtenemos la función de Blackman. Pero, ¿por qué exactamente 0,42? Para responder a esta pregunta, necesitamos trazar su espectro. La Transformada Analítica de Fourier no es una tarea fácil, pero Wolfram también puede manejarla, salvándonos de la tarea.



hx = Function[{x, a},

Piecewise[{{f[x] /. ss[[1]], -1/2 < x < 1/2}}, 0] // Evaluate]

hw = Function[{w, a}, 
  FourierTransform[hx[x, a], x, w] // #/Limit[#, w -> 0] & // 
    Simplify // Evaluate]

↓









De esta forma, el gráfico de la función todavía no es muy informativo, ya que es más conveniente analizar el espectro en una escala logarítmica. Añadiendo la conversión apropiada a decibelios$$$20 \log _{10}(\left| x\right| )$, obtenemos el mismo gráfico habitual del espectro de funciones de ventana:









En el proceso de cambio de parámetro observaremos algo similar:







Dependiendo del parámetro a, el nivel de los lóbulos laterales cambia, y a a = 0,42 es más o menos mínimo y uniforme. Con a = 0,409, podemos obtener un resultado ligeramente mejor si por “mejor” nos referimos al nivel mínimo posible de lóbulos laterales.

Desarrollo

Obviamente, tal microoptimización no valió la pena el esfuerzo. ¿Es posible mejorar cualitativamente las propiedades de esta ventana sin cambiar los datos iniciales?



Anteriormente, analizamos la salida de las funciones de ventana que suman uno, lo que le permite restaurar la señal original. Probemos esta técnica para nuestra ventana y veamos cómo afecta el espectro.



Definamos una función auxiliar para construir ventanas superpuestas, teniendo en cuenta los límites del argumento en el rango de -1/2 a 1/2:







Encuentre la antiderivada, muévala al centro de coordenadas y escale a uno:





↓





mostrarla en el gráfico:







Como puede ver, Wolfram lo hizo solo aquí también, y no tuvimos que establecer manualmente una definición continua por partes de una antiderivada. Ahora, la vista de nuestra ventana depende no solo de la variable a , sino del grado de superposición, y a medida que aumenta, tenderá a la forma de la derivada:







Y el toque final es encontrar una función analítica para el espectro con el fin de determinar el valor óptimo del parámetro a .



Aquí, si intentamos calcular la transformación directamente, como la última vez, llevaremos a Wolfram a un pensamiento profundo. Hay varias formas de acelerar este proceso:



- use una transformación discreta en lugar de una analítica - la más simple. Pero un verdadero matemático no aplicará métodos numéricos donde se pueda encontrar una solución puramente analítica, y nosotros no lo haremos (todavía); además, tiene limitaciones obvias (en términos de resolución y limitación de espectro);



- pasar valores específicos como un parámetro de superposición y, mirando los resultados, intentar ver el patrón y generalizarlos. Una opción bastante funcional, pero que requiere esfuerzos mentales y creativos adicionales. Dejémoslo como último recurso.



- realizar cálculos directamente en el dominio de la frecuencia. Esto es posible debido a las siguientes propiedades de la transformada de Fourier:



1) es lineal, es decir la suma de las imágenes es igual a la imagen de la suma;

2) la integración en el dominio del tiempo es equivalente a dividir por iw en el dominio de la frecuencia.

3) el desplazamiento en el tiempo es equivalente a la modulación con una sinusoide compleja.

(más en wikipedia o aquí ).



Por lo tanto, teniendo el espectro hw de una función de ventana arbitraria, podemos obtener de él el espectro hwo de una función sumada a uno con t superpuesto :





↓





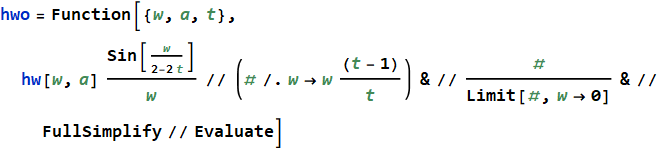
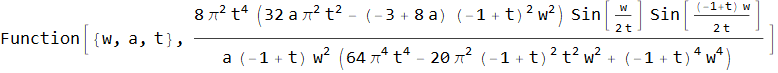
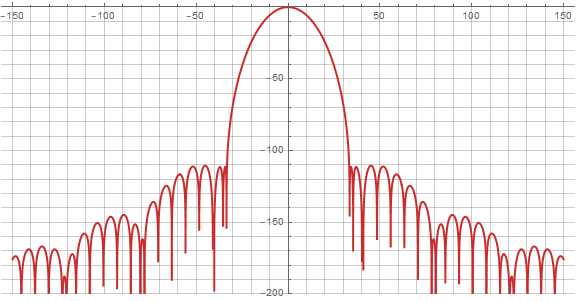
Ahora podemos ver cómo cambia el espectro en dinámica:







Aquí, cambiar el parámetro de superposición ya afectará al espectro de ventana de una manera ligeramente diferente :







Habiendo jugado un poco con los parámetros, es fácil notar que “más grande no es mejor”, y el grado óptimo de superposición para esa función está en la región de cuatro. Específicamente, para t = 4 y a= 0,404 obtenemos que el nivel del lóbulo lateral no supere los -80 dB. Este es un muy buen resultado, especialmente considerando que la función coseno elevado, usada tradicionalmente para ventanas sumadas, da un nivel de lóbulo de aproximadamente -30 dB. Bueno, cuando se escribe explícitamente, nuestra nueva función de ventana se verá así:

$$

$$\left\{ \begin{array}{ll} \frac{404 \pi (1-2 x)+36 \sin \left(\frac{1}{3} (16 \pi x+\pi )\right)+375 \sin \left(\frac{1}{3} (\pi -8 \pi x)\right)}{606 \pi } & \frac{1}{4} < x \leq \frac{1}{2} \\ \frac{404 (2 \pi x+\pi )+36 \sin \left(\frac{2}{3} \pi (8 x+1)\right)+375 \sin \left(\frac{1}{3} (8 \pi x+\pi )\right)}{606 \pi } & -\frac{1}{2} < x \leq -\frac{1}{4} \\ \frac{\sqrt{3} \left(125 \cos \left(\frac{8 \pi x}{3}\right)+12 \cos \left(\frac{16 \pi x}{3}\right)\right)}{202 \pi }+\frac{1}{3} & -\frac{1}{4} < x \leq \frac{1}{4} \\ 0 & \left| x\right| >\frac{1}{2} \\ \end{array} \right.$$

Mayor desarrollo

¿Qué más puede hacer para reducir aún más el nivel de los lóbulos laterales? Puede tomar cosenos no con frecuencias pares, sino con frecuencias impares (aquí, por compacidad, la solución del sistema de ecuaciones está incrustada directamente en la definición de la función):

$$

$$\left(a \cos (\pi x)+\left(\frac{5}{8}-\frac{a}{2}\right) \cos (3 \pi x)+\left(\frac{3}{8}-\frac{a}{2}\right) \cos (5 \pi x)\right) \Pi (x)$$

y tras la integración con los parámetros a = 0,6628 y un nivel de superposición de 4,5, obtener una atenuación de -90 dB:







Explícitamente:

$$

$$\small\left\{ \begin{array}{ll} \frac{327 \sin \left(\frac{1}{7} \pi (45 x+2)\right)+24855 \sin \left(\frac{1}{7} \pi (1-9 x)\right)+3670 \cos \left(\frac{1}{14} \pi (54 x+1)\right)+21512}{43024} & \frac{5}{18} < x \leq \frac{1}{2} \\ \frac{24855 \sin \left(\frac{1}{7} \pi (9 x+1)\right)+3670 \sin \left(\frac{3}{7} \pi (9 x+1)\right)+327 \sin \left(\frac{5}{7} \pi (9 x+1)\right)+21512}{43024} & -\frac{1}{2} < x \leq -\frac{5}{18} \\ \begin{array}{ll} \frac{-3670 \sin \left(\frac{3}{7} \pi (9 x-1)\right)+24855 \sin \left(\frac{1}{7} \pi (9 x+1)\right)+327 \sin \left(\frac{5}{7} \pi (9 x+1)\right)}{43024}+ \\ +\frac{3670 \sin \left(\frac{3}{7} \pi (9 x+1)\right)+327 \sin \left(\frac{1}{7} \pi (45 x+2)\right)+24855 \sin \left(\frac{1}{7} \pi (1-9 x)\right)}{43024} \end{array} & -\frac{5}{18} < x \leq \frac{5}{18} \\ 0 & \left| x\right| >\frac{1}{2} \\ \end{array} \right.$$

Puede agregar un coseno más y aumentar el número de derivadas cero:

$$

$$\left(a \cos (\pi x)+\frac{1}{80} (35-16 a) \cos (3 \pi x)+\frac{1}{80} (35-48 a) \cos (5 \pi x)+\frac{1}{40} (5-8 a) \cos (7 \pi x)\right) \Pi (x)$$

y después de la integración con los parámetros a = 0.5862 y un nivel de superposición de 6.4 para obtener una supresión de -110 dB:







Explícitamente:

$$

$$\small\left\{ \begin{array}{ll} \frac{-3077550 \sin \left(\frac{1}{54} \pi (64 x-5)\right)-90069 \sin \left(\frac{5}{54} \pi (64 x-5)\right)-5820 \sin \left(\frac{7}{54} \pi (64 x-5)\right)-560455 \cos \left(\frac{1}{9} \pi (7-32 x)\right)+2601344}{5202688} & \frac{11}{32}< x \leq \frac{1}{2} \\ \frac{560455 \sin \left(\frac{1}{18} \pi (64 x+5)\right)+3077550 \sin \left(\frac{1}{54} \pi (64 x+5)\right)+90069 \sin \left(\frac{5}{54} \pi (64 x+5)\right)+5820 \sin \left(\frac{7}{54} \pi (64 x+5)\right)+2601344}{5202688} & -\frac{1}{2}< x \leq -\frac{11}{32} \\ \begin{array}{ll} \frac{-3077550 \sin \left(\frac{1}{54} \pi (64 x-5)\right)-90069 \sin \left(\frac{5}{54} \pi (64 x-5)\right)-5820 \sin \left(\frac{7}{54} \pi (64 x-5)\right)-560455 \cos \left(\frac{1}{9} \pi (7-32 x)\right)}{5202688}+ \\ +\frac{560455 \sin \left(\frac{1}{18} \pi (64 x+5)\right)+3077550 \sin \left(\frac{1}{54} \pi (64 x+5)\right)+90069 \sin \left(\frac{5}{54} \pi (64 x+5)\right)+5820 \sin \left(\frac{7}{54} \pi (64 x+5)\right)}{5202688} \end{array} &-\frac{11}{32}< x \leq \frac{11}{32} \\ 0 & \left| x\right| >\frac{1}{2} \\ \end{array} \right.$$

Se puede lograr una reducción aún más significativa en el nivel de lóbulos laterales elevando al cuadrado la transformada de Fourier y reduciendo así el nivel de lóbulos laterales en un factor de 2 a la vez. Esto le permite deshacerse del aumento en el número de parámetros para su selección manual, pero agrega complejidad al calcular la convolución en el dominio del tiempo.









y aquí ya es posible lograr una supresión de más de 160 dB:







no daremos la fórmula explícitamente debido a su impresionante tamaño.

Funciones de ventana hipergeométrica

Para asegurar el número requerido de ceros en los límites de nuestra función, usamos una búsqueda a través de la solución de un sistema de ecuaciones con integración posterior. Esto no es muy conveniente: debe cambiar el número de ecuaciones cada vez. ¿Quizás haya una solución más simple y hermosa? ¡Ahi esta! Y la función hipergeométrica nos ayudará con esto.





Nuestra solución se verá así:

$$

$$\frac{2 z \Gamma \left(\frac{n+3}{2}\right) \, _2F_1\left(\frac{1}{2},-\frac{n}{2};\frac{3}{2};z^2\right)}{\sqrt{\pi } \Gamma \left(\frac{n}{2}+1\right)}+a \left(z+b z^3\right) \left(1-z^2\right)^{n/2}$$

Dónde $$$z=\sin \left(\frac{\pi x}{2}\right)$



Consiste en la suma de dos partes: la antiderivada de la función $$$\left(1-z^2\right)^{\frac{n}{2}}$, normalizada en amplitud al punto (1,1) y una función con parámetros libres, multiplicada por la misma $$$\left(1-z^2\right)^{\frac{n}{2}}$para preservar el número requerido de derivadas cero: La







precisión del ajuste y su influencia en la distribución de los lóbulos laterales dependerá de la función que elijamos para corregir la forma; existen opciones posibles que requieren estudios separados. En este caso, la función$$$a \left(z+b z^3\right)$ofrece una opción bastante aceptable y, debido a dos parámetros, le permite realizar ajustes más precisos.



La fórmula en sí es interesante (y conveniente) porque para n par se simplifica a un polinomio, y para n impar se simplifica a la suma de un polinomio con arcoseno y raíz cuadrada, lo que hace que la fórmula final sea más compacta y más fácil de calcular.



Ya es más fácil (y más rápido) seleccionar los parámetros aquí a través de la transformada discreta de Fourier. También necesitamos una definición adicional de la función de superposición para trabajar con tres parámetros:



















Como ejemplo, después de sustituir los parámetros de la imagen, nuestra función se simplificará a

$$

$$\frac{-288 z^{11}+2315 z^9-7380 z^7+12330 z^5-11940 z^3+8163 z}{3200}$$

Ventana de Kaiser inverso

Si la tarea de sumar las ventanas en una no vale la pena, entonces la ventana más óptima es la ventana de Kaiser, que le permite ajustar sin problemas el ancho del lóbulo principal. Sin embargo, tiene un inconveniente: dado que se expresa en términos de la función de Bessel , es algo difícil de leer fuera de los paquetes matemáticos. Por supuesto, puede implementar la función Bessel por separado, o también puede buscar una aproximación a través de funciones elementales. Y de repente resultó que al usar la función del espectro de la ventana de Kaiser (limitada en el tiempo) para esto, puede obtener un resultado incluso un poco mejor:

$$

$$\frac{ \sinh \left(k \sqrt{1-4 x^2}\right)}{\sinh (k) \sqrt{1-4 x^2} } \Pi (x)$$

El pago por una decisión tan astuta fue la imposibilidad de expresar su espectro de forma puramente analítica, pero esto no es tan importante, ya que en la práctica, en cualquier caso, operamos y analizamos datos en forma discreta utilizando la transformada discreta de Fourier. A continuación, en el gráfico, puede comparar sus espectros, donde el rojo es la ventana original de Kaiser, el verde es su aproximación:









Con el mismo ancho del pétalo principal, el nivel de los lóbulos laterales es ligeramente más bajo. Y para facilitar su uso, puede elaborar una tabla con valores aproximados del parámetro k para obtener el nivel requerido de supresión de lóbulos laterales:

$$

$$\begin{array}{cc} \text{-60 } & \text{k=8.8} \\ \text{-90 } & \text{k=11.36} \\ \text{-120 } & \text{k=15.18} \\ \text{-150 } & \text{k=18.88} \\ \end{array}$$

Encontrar una aproximación de la antiderivada de la ventana de Kaiser inversa sigue siendo un problema interesante aparte. Hasta ahora, solo ha sido posible expresarlo a través de una serie de potencias, que converge con bastante lentitud:

$$

$$\small \int \frac{ \sinh \left(k \sqrt{1-4 x^2}\right)}{\sinh (k) \sqrt{1-4 x^2} } \, dx= \sum _{n=1}^{\infty } -\frac{2^{\frac{1}{2}-n} k^{n-1} x^{2 n-1} \left(\sqrt{-k} (-1)^n K_{n-\frac{1}{2}}(-k)+\sqrt{k} K_{n-\frac{1}{2}}(k)\right)}{\sqrt{\pi } (2 n-1) \sinh (k) \Gamma (n)}$$

Quizás los expertos en matemáticas puedan sugerir una mejor solución en los comentarios.

Conclusión

A pesar de que el procesamiento de señales digitales es una disciplina completamente formada, todavía hay espacio para el desarrollo y algo nuevo en él; al menos en la literatura especial y científica existente, no se consideran los problemas de la construcción de funciones de ventana resumidas en una unidad; y las capacidades de los sistemas de álgebra computacional modernos permiten repensar el conocimiento acumulado a un nivel cualitativamente nuevo.



El documento original de Wolfram Mathematica con todos los cálculos está disponible en GitHub .