problema de Goldbach El problema de Goldbach es el enunciado de que cualquier número par, que comience con 4, se puede representar como la suma de dos primos. Es decir, 6 = 3 + 3; 8 = 5 + 3 ... Según tengo entendido, la solución al problema es una prueba o refutación de esta afirmación.
Lo primero que debemos hacer es implementar un método para verificar si un número es primo. Un primo es un número que es divisible solo por sí mismo y por uno.
public static bool IsPrimeNumber(ulong n)
{
var result = true;
if (n > 1)
{
for (ulong i = 2; i < n; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
}
else
{
result = false;
}
return result;
}
Ahora necesitamos obtener una colección de todos los números primos hasta ulong.MaxValue = 18446744073709551615 (2 ^ 64-1)
public static IEnumerable<ulong> GetAllPrimeNumbers(ulong maxNumber)
{
List<ulong> primeNumbers = new List<ulong>();
for (ulong i=0; i < maxNumber; i++ )
{
if (IsPrimeNumber(i))
{
primeNumbers.Add(i);
}
}
return primeNumbers;
}
La intuición sugiere que tomará mucho tiempo calcularlos, por lo que reduciremos su número a 300,000
static void Main(string[] args)
{
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
IEnumerable<ulong> primeNumbers = GetAllPrimeNumbers();
checkGoldbach(primeNumbers);
stopwatch.Stop();
Console.WriteLine(" " + stopwatch.Elapsed.TotalSeconds + " ");
foreach(var number in primeNumbers)
{
Console.Write(number + " ");
}
Console.ReadKey();
}

Luego quería encontrar todos los números primos hasta 2 ^ 64 (me pareció que un par de horas de cálculos serían suficientes para mí)
Después de dos minutos de ejecutar el programa, decidí poner un punto de interrupción y verificar qué número se está verificando para simplificar:
411780 iteraciones después de dos minutos de cálculos. Decidí optimizar ligeramente el método para comprobar la simplicidad de un número, ya que no es necesario seguir iterando después de la mitad del número
, por lo que el número de iteraciones necesarias para comprobar la simplicidad se reduce a la mitad. Me pareció que en 2 minutos el número de iteraciones debería duplicarse

Pero aquí también me equivoqué. La productividad aumentó no en un 100%, sino en un 22%. Como entendí más tarde, esto se debe al hecho de que la mitad de los cheques, como antes, se eliminan al dividir por 2, un tercio de todos los números que no se eliminan al dividir por 2 se eliminan al dividir por 3, etc. De las 500154 pruebas de simplicidad, se encontraron 41549 primos. Es decir, la iteración
for (ulong i = 2; i <= n/2; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
ejecutado hasta el final (sin interrupción) solo 41,549 veces. En otros casos, se interrumpió antes ...
500154 y no casi 2 ^ 64, debe calcular cuánto tiempo tomará verificar la simplicidad de todos los números a 2 ^ 64
Primero, reduzcamos el número de iteraciones de 2 ^ 64 a 30000 y calculemos el tiempo de ejecución del método del cronómetro

para iterar números hasta 30.000, se gastó 1 segundo
ahora hagamos una tabla con otros valores del número de iteraciones
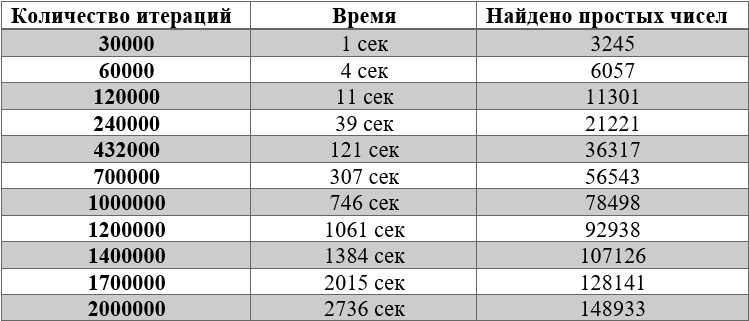
Escribamos el resultado en Excel y construyamos un gráfico de puntos para las coordenadas "Número de iteraciones por tiempo" y "Número de primos por rango"
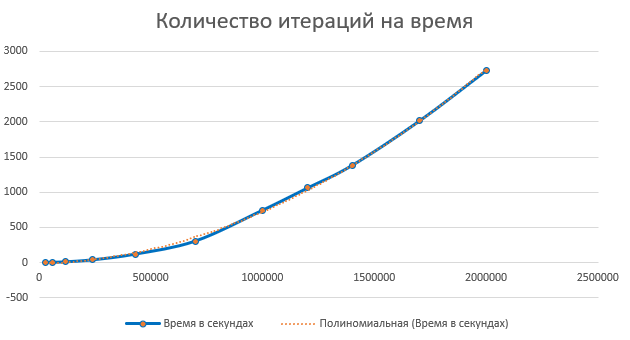
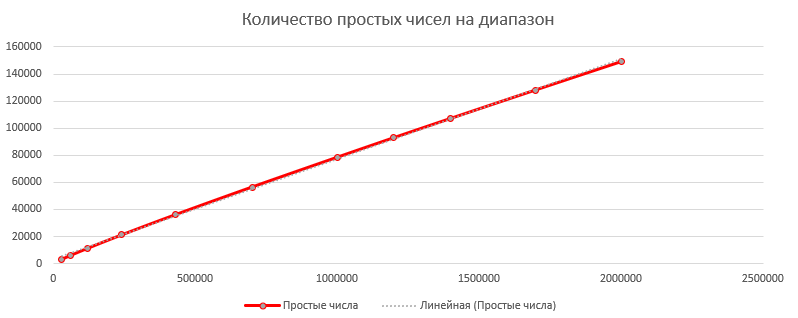
Ahora podemos averiguar el número aproximado de primos hasta 2 ^ 64, y aproximadamente cuánto tiempo llevará encontrarlos todos
Si agrega una línea de tendencia "lineal" al gráfico de "números primos por rango", Excel le dará la fórmula y = 0.074x + 3004 (no sé qué tan precisa es la fórmula). Esto significa que el número aproximado de números primos hasta ulong.MaxValue = 0.074 * 2 ^ 64 + 3004;
De la misma forma, sumando la línea de tendencia "Polinomio" al gráfico "Número de iteraciones en el tiempo", obtenemos la fórmula y = 7E-10x2 + 6E-05x. Sustituyendo nuestro número 2 ^ 64 en lugar de x, puede descubrir que para encontrar todos los números primos hasta 2 ^ 64, necesitamos aproximadamente 2.38E + 29 segundos, o 7553198149564240000000 años. Ok, no puedo esperar tanto.
Intentemos demostrar que la conjetura de Goldbach es cierta para todos los números pares hasta 300.000.
public static void checkGoldbach(IEnumerable<ulong> primeNumbers)
{
ulong numbersCount = 300000;
for (ulong number = 4; number<numbersCount; number+=2)
{
bool isGoldbachResult = false;
foreach(ulong primeNumber1 in primeNumbers)
{
foreach(ulong primeNumber2 in primeNumbers)
{
if(primeNumber1+primeNumber2==number)
{
Console.WriteLine("{0} = {1} + {2}", number, primeNumber1, primeNumber2);
isGoldbachResult = true;
break;
}
if(primeNumber1+primeNumber2>number)
{
break;
}
}
if(isGoldbachResult|| primeNumber1>number)
{
break;
}
}
if(!isGoldbachResult)
{
Console.WriteLine(" " + number + " ");
break;
}
}
}
Si la afirmación de Goldbach no es cierta para algún número, el método dejará de calcular en ese número.
Después de 9 minutos de cálculos, podemos decir que la hipótesis de Goldbach es válida para números menores a 300.000.
Total
Todo resultó no ser tan simple como me parecía al principio, y entiendo que no estoy nada cerca de resolver el problema.
Lo más probable es que me parezca que hay mejores opciones para verificar un número por simplicidad. Es posible que el método que verifica la exactitud de los números pares para la afirmación de Goldbach pueda implementarse de manera más racional que una simple enumeración de números primos, pero ya no quiero dedicar tanto tiempo a esto ...
Resolver el problema de Goldbach no le dará nada a la humanidad. Hasta ahora, se ha demostrado que la hipótesis es cierta para números hasta 4 * 10 ^ 18, pero ¿cuál es el punto de probarla para todos los números? ¿Con qué propósito los matemáticos escriben libros sobre este tema y generalmente dedican su tiempo a resolver tales "problemas"?
Realmente quiero preguntar a las personas conocedoras si mi fórmula para calcular el número de números primos por rango tiene derecho a existir.
PD
Lo más probable es que no necesite escribir artículos de los que sepa poco. No esperaba que la comunidad reaccionara de esta manera. Pero no pretendí que mi decisión fuera la única correcta. Soy un aficionado en este campo.
¿Con qué propósito escribí este artículo?
Me tomé el tiempo para investigar esta pregunta y me pareció que a algunas personas les podría gustar. Fue interesante para mí porque es una tarea divertida. Pero, ¿por qué los matemáticos pierden el tiempo en esto? Sinceramente, no entiendo el beneficio real de investigar específicamente estas preguntas.
PPS
Después de leer las reseñas sobre el artículo, decidí sacar conclusiones.
Lo más probable es que me parezca que hay mejores opciones para verificar un número por simplicidad
Según lo sugerido por los usuarios dvserg dr Por qué y Pavel_The_Bestrealmente es. Por ejemplo, usando el tamiz de Eratosthenes, se puede recolectar una colección de primos mucho más rápido. Aquí están los artículos que puedes leer sobre este tema: Algoritmo para verificar la simplicidad en O (log N) , Wikipedia , puedes leer los trabajos de Srinivas Ramanujan Iyengor
¿Tiene derecho a existir mi fórmula para calcular la cantidad de números primos por rango?
No
¿Resolver el problema de Goldbach no aportará nada a la humanidad?
Mi opinión de que algunos problemas matemáticos son inútiles provocó una actitud muy negativa por parte de la mayoría de los usuarios. Usuariosvvadzim Nevera bromzh Gráfico en Nevera EimKR bfDesarrollador y sípudieron convencerme de esto. Retiro mis palabras.
Desde la antigüedad, los matemáticos han estado buscando la verdad y su búsqueda a menudo conduce a consecuencias beneficiosas para el progreso. Quizás el problema en sí y su solución no le den nada al mundo aquí y ahora, pero son las conclusiones extraídas durante la búsqueda de una solución las que pueden ser útiles a largo plazo.