🍃 🔣 🎅🏾 Mover un objeto uniformemente a lo largo de una curva 🐅 🙎🏻 😦

En el proceso de desarrollo de un juego en categorías de género completamente diferentes, puede ser necesario "lanzar" cualquier objeto del juego a lo largo de una curva suave a una velocidad constante o controlada, ya sea un camión que se mueve de la ciudad A a la ciudad B, un misil disparado a lo largo de una trayectoria astuta o un avión enemigo. realizando una maniobra tendida.

Probablemente, todos los relacionados con el tema conocen o al menos han oído hablar de las curvas de Bézier, B-splines, Hermite splines y otras interpolaciones y suavizado de splines y sugerirían absolutamente correctamente usar uno de ellos en la situación descrita, pero no todo es tan simple. como nos gustaría.

En nuestro caso, una spline es una función que muestra un conjunto de parámetros de entrada (puntos de control) y el valor de un argumento.

t

$t$ (generalmente tomando valores de 0 a 1) a un punto en un plano o en el espacio. La curva resultante es el conjunto de valores de la función spline para

t \in [0, 1]

$t\in[0,1]$ ...

Como ejemplo, considere la curva de Bezier cúbica , que viene dada por la siguiente ecuación:

$imagen$

Curva de Bézier cúbica

La figura muestra dos curvas de Bézier cúbicas, definidas por cuatro puntos (la curva pasa por dos de ellos, los dos restantes definen la curvatura).

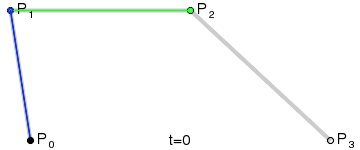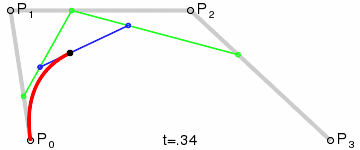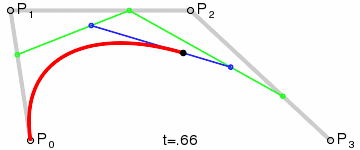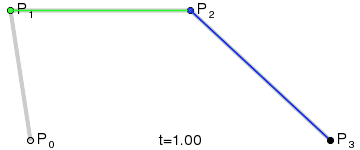
imagen

Animación de mostrar el parámetro t en un punto de la curva

Para construir una ruta más compleja y variable a partir de las secciones de la curva, se pueden conectar en una cadena, dejando un punto-enlace común:

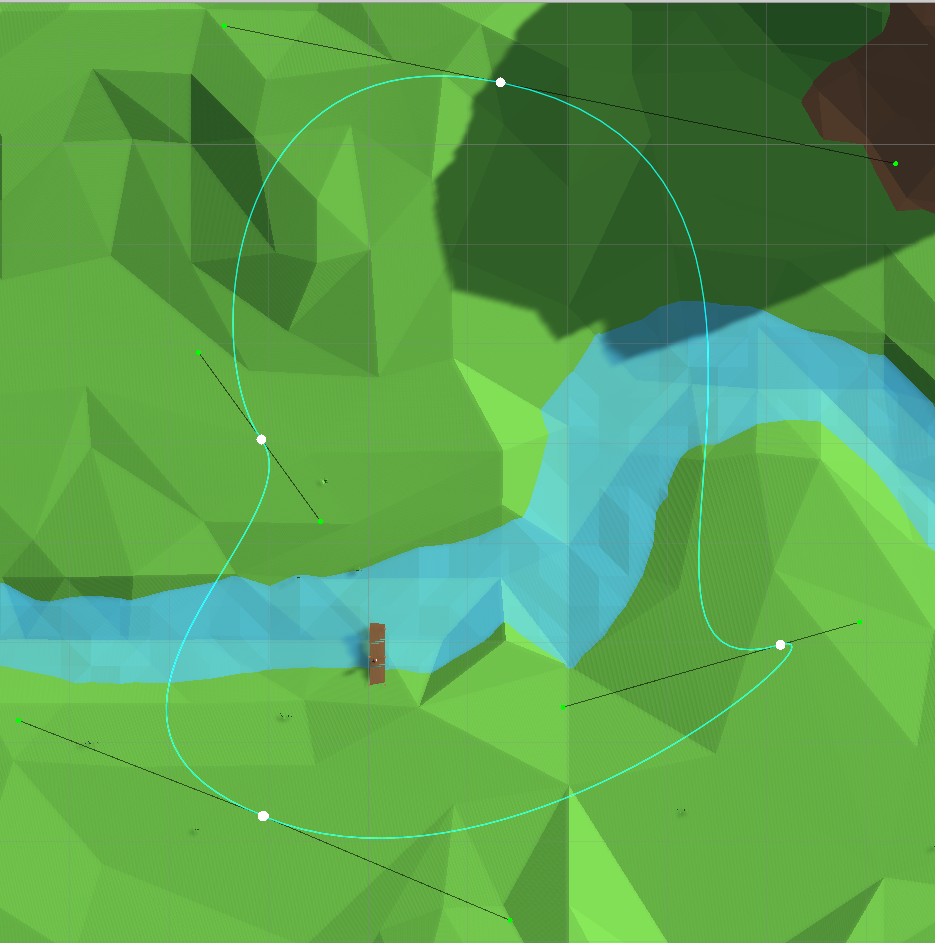
Tramo por partes Hemos

descubierto la tarea y la parametrización de la ruta, ahora pasamos a la pregunta principal. Para que nuestro avión convencional se mueva a lo largo de la ruta a una velocidad constante, necesitamos en cualquier momento poder calcular un punto en la curva en función de la distancia recorrida a lo largo de esta curva.

s (l e n)

$s(len)$ , teniendo solo la capacidad de calcular la posición de un punto en la curva a partir del valor del parámetro

t

$t$ (función

y (t)

$y(t)$ ). Es en esta etapa que comienzan las dificultades.

Mi primer pensamiento fue hacer un mapeo lineal

l e n \in [0, L e n g t h] \Rightarrow t \in [0, 1]

$len\in[0, Length] \Rightarrow t\in[0,1]$ y calcular

y (t)

$y(t)$ del valor resultante: fácil, computacionalmente económico, en general, lo que necesita.

imagen

El problema con este método es inmediatamente obvio; de hecho, la distancia recorrida

s

$s$ depende de

t

$t$ de forma no lineal, y para estar convencido de ello, basta con disponer a lo largo de la ruta distribuidos uniformemente

t

$t$ puntos: puntos

distribuidos "uniformemente" a lo largo de la trayectoria

La aeronave ralentizará en algunos tramos y acelerará en otros, lo que hace que este método de parametrización de la curva sea completamente inaplicable para resolver el problema descrito (el avión se eligió exclusivamente como ejemplo ilustrativo y no se persiguió el objetivo de describir su movimiento de manera físicamente correcta ):

Visualización de parametrización incorrecta de la curva

Después de consultar el buscador, en stackoverflow y youtube , encontré una segunda forma de calcular

s (l e n) = g (t)

$s(len) = g(t)$ , es decir, la representación de la curva en forma de una función lineal por partes (calculando un conjunto de puntos equidistantes entre sí a lo largo de la curva):

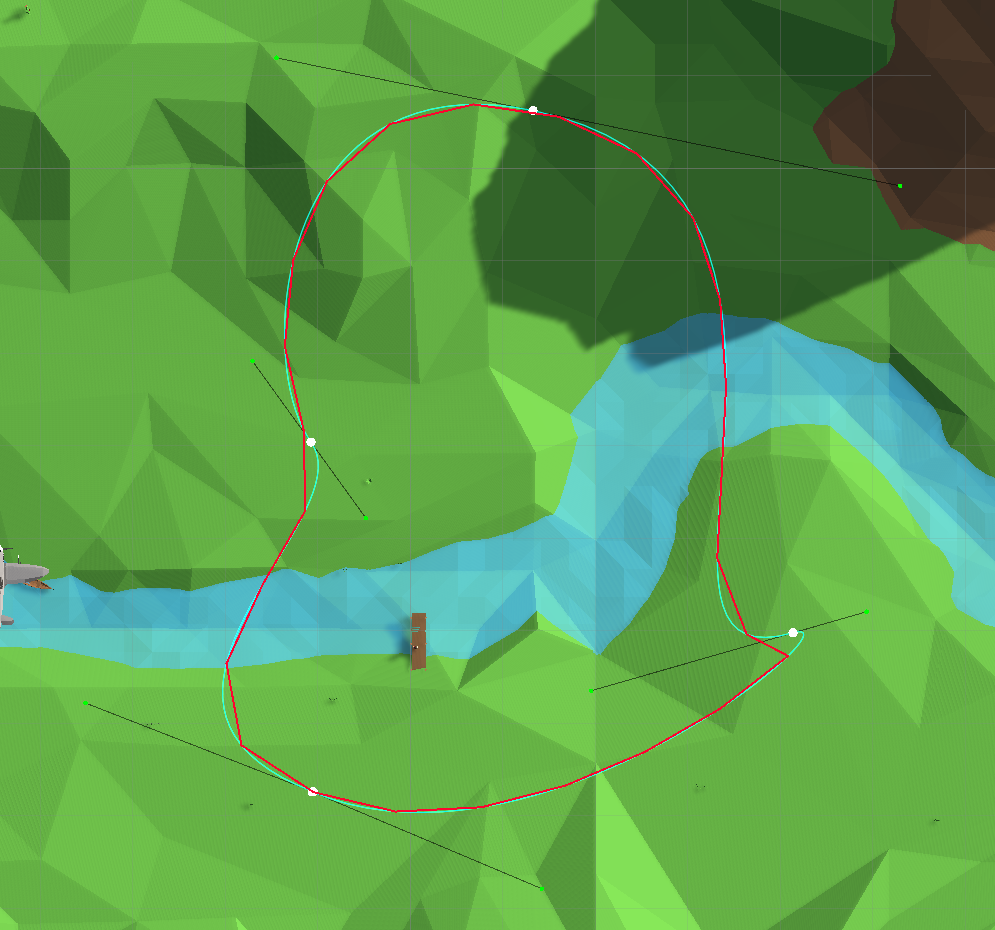
Representar la curva en forma de spline lineal por partes

Este procedimiento es iterativo: se da un pequeño paso

t

$t$ , nos movemos a lo largo de una curva con él, sumando la distancia recorrida como la longitud de una spline lineal por partes hasta que se cubre la distancia especificada, después de lo cual se recuerda el punto y se reanuda el proceso.

Código de muestra

Una fuente

public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)
  {
    List<Vector2> evenlySpacedPoints = new List<Vector2>();
    evenlySpacedPoints.Add(points[0]);
    Vector2 previousPoint = points[0];
    float dstSinceLastEvenPoint = 0;

    for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)
    {
      Vector2[] p = GetPointsInSegment(segmentIndex);
      float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);
      float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;
      int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);
      float t = 0;
      while (t <= 1)
      {
        t += 1f/divisions;
        Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);
        dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);

        while (dstSinceLastEvenPoint >= spacing)
        {
          float overshootDst = dstSinceLastEvenPoint - spacing;
          Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;
          evenlySpacedPoints.Add(newEvenlySpacedPoint);
          dstSinceLastEvenPoint = overshootDst;
          previousPoint = newEvenlySpacedPoint;
        }

        previousPoint = pointOnCurve;
      }
    }

    return evenlySpacedPoints.ToArray();
  }

Y, al parecer, el problema está resuelto, porque puede dividir la ruta en muchos segmentos y disfrutar de lo suave y medido que se mueve el objeto, ya que calcular un punto en una función lineal por partes es una cuestión simple y rápida. Pero este enfoque también tiene inconvenientes bastante obvios que me molestaron: un procedimiento bastante costoso para cambiar el paso de la partición o la geometría de la curva y la necesidad de encontrar un equilibrio entre la precisión (más consumo de memoria) y el ahorro de memoria (la ruta "rota" se vuelve más notoria).

Como resultado, continué buscando y encontré un excelente artículo "Moverse a lo largo de una curva con velocidad especificada" , sobre cuya base se basa el razonamiento adicional.

El valor de velocidad se puede calcular como

σ (t) = | V (t) | = | \frac{d X}{d t} |

$\sigma(t) = |V(t)|=|\frac{dX}{dt}|$ dónde

X (t)

$X(t)$ - función spline. Para resolver el problema, necesita encontrar la función

Y (t) = X (s)

$Y(t)=X(s)$ dónde

s

$s$ - la longitud del arco desde el punto de inicio hasta el deseado, y esta expresión establece la relación entre

t

$t$ y

s

$s$ ...

Usando la sustitución de variables de diferenciación, podemos escribir

\frac{d Y}{d t} = \frac{d X}{d s} \frac{d s}{d t} .

$\frac{dY}{dt}=\frac{dX}{ds}\frac{ds}{dt}.$

Teniendo en cuenta que la velocidad es una cantidad no negativa, obtenemos

| \frac{d Y}{d t} | = | \frac{d X}{d s} | | \frac{d s}{d t} | = \frac{d s}{d t},

$|\frac{dY}{dt}|=|\frac{dX}{ds}||\frac{ds}{dt}|=\frac{ds}{dt},$

porque

| \frac{d X}{d s} | = 1

$|\frac{dX}{ds}| = 1$ por la condición de que el módulo del vector de velocidad permanezca sin cambios (en términos generales,

| \frac{d X}{d s} |

$|\frac{dX}{ds}|$ no es igual a uno, sino a una constante, pero para simplificar los cálculos, tomaremos esta constante igual a uno).

Ahora obtenemos la relación entre

t

$t$ y

s

$s$ explícitamente:

s = g (t) = \int_{0}^{t} | \frac{d Y (τ)}{d t} | d τ,

$s=g(t)=\int_{0}^{t}|\frac{dY(\tau)}{dt}|d\tau,$

de donde la longitud total de la curva

L

$L$ obviamente se calcula como

g (1)

$g(1)$ ... Usando la fórmula resultante, es posible, teniendo el valor del argumento

t

$t$ , calcula la longitud del arco hasta el punto en el que este valor es

t

$t$ se visualiza.

Nos interesa la operación inversa, es decir, calcular el valor del argumento

t

$t$ a lo largo de una longitud de arco dada

s

$s$ :

t = g^{- 1} (s) .

$t=g^{-1}(s).$

Dado que no existe una forma analítica general de encontrar la función inversa, tendrá que buscar una solución numérica. Denotamos

F (t) = g (t) - s .

$F(t)=g(t)-s.$ Para una dada

s

$s$ , es necesario encontrar ese valor

t

$t$ en el cual

F (t) = 0

$F(t)=0$ ... Por lo tanto, la tarea se convirtió en la tarea de encontrar la raíz de la ecuación, que el método de Newton puede manejar perfectamente.

El método forma una secuencia de aproximaciones de la forma

t_{i + 1} = t_{i} - \frac{F (t_{i})}{F^{'} (t_{i})},

$t_{i+1}=t_i-\frac{F(t_i)}{F'(t_i)},$

Dónde

F^{'} (t) = \frac{d F}{d t} = \frac{d g}{d t} = | \frac{d Y}{d t} | .

$F'(t)=\frac{dF}{dt}=\frac{dg}{dt}=|\frac{dY}{dt}|.$

Calcular

F (t)

$F(t)$ Necesito calcular

g (t)

$g(t)$ , cuyo cálculo, a su vez, requiere integración numérica.

Elección

t_{0} = \frac{s}{L}

$t_0=\frac{s}{L}$ como una aproximación inicial ahora parece razonable (recuerde el primer enfoque para resolver el problema).

A continuación, iteramos usando el método de Newton hasta que el error de solución se vuelve aceptable o el número de iteraciones realizadas es prohibitivamente grande.

Existe un problema potencial al utilizar el método estándar de Newton. Función

F (t)

$F(t)$ - no decreciente, ya que su derivada

F^{'} (t) = | d Y / d t |

$F'(t)=|dY/dt|$ no es negativo. Si la segunda derivada

F^{″} (t) > 0

$F''(t)>0$ , entonces la función se llama convexa y se garantiza que el método de Newton convergerá a la raíz. Sin embargo, en nuestro caso,

F^{″} (t)

$F''(t)$ puede resultar negativo, por lo que el método de Newton puede converger fuera del rango de definición

t \in [0, 1]

$t\in[0,1]$ ... El autor del artículo propone utilizar una modificación del método de Newton, que, si el resultado de la siguiente iteración por el método de Newton no cae en el intervalo actual que limita la raíz, en su lugar selecciona el medio del intervalo ( método de dicotomía ). Independientemente del resultado del cálculo en la iteración actual, el rango se reduce, lo que significa que el método converge a la raíz.

Queda por elegir el método de integración numérica: utilicé las cuadraturas del método de Gauss , ya que proporciona un resultado bastante preciso a bajo costo.

Código de función para calcular t (s)

public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);

private float Parameter(float length)
{
  float t = 0 + length / ArcLength(1);
  float lowerBound = 0f; 
  float upperBound = 1f;

  for (int i = 0; i < 100; ++i)
  {
    float f = ArcLength(t) - length;

    if (Mathf.Abs(f) < 0.01f)
      break;

    float derivative = TangentMagnitude(t);
    float candidateT = t - f / derivative;

    if (f > 0)
    {
      upperBound = t;
      if (candidateT <= 0)
        t = (upperBound + lowerBound) / 2;
      else
        t = candidateT;
    }
    else
    {
      lowerBound = t;
      if (candidateT >= 1)
        t = (upperBound + lowerBound) / 2;
      else
        t = candidateT;
    }
  }
  return t;
}

Código de función de integración numérica

private static readonly (float, float)[] CubicQuadrature =
{(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};

public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound)
{
  var sum = 0f;
  foreach (var (arg, weight) in CubicQuadrature)
  {
    var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));
    sum += weight * f(t);
  }

  return sum * (upperBound - lowerBound) / 2;
}

A continuación, puede ajustar el error del método de Newton, elegir un método más preciso de integración numérica, pero el problema, de hecho, está resuelto: se construyó un algoritmo para calcular el argumento

t

$t$ spline para una longitud de arco determinada. Combinar varias secciones de curvas en una y escribir un procedimiento de cálculo generalizado

s (t)

$s(t)$ puede almacenar las longitudes de todos los segmentos y calcular previamente el índice del segmento donde desea realizar un procedimiento iterativo utilizando el método de Newton modificado.

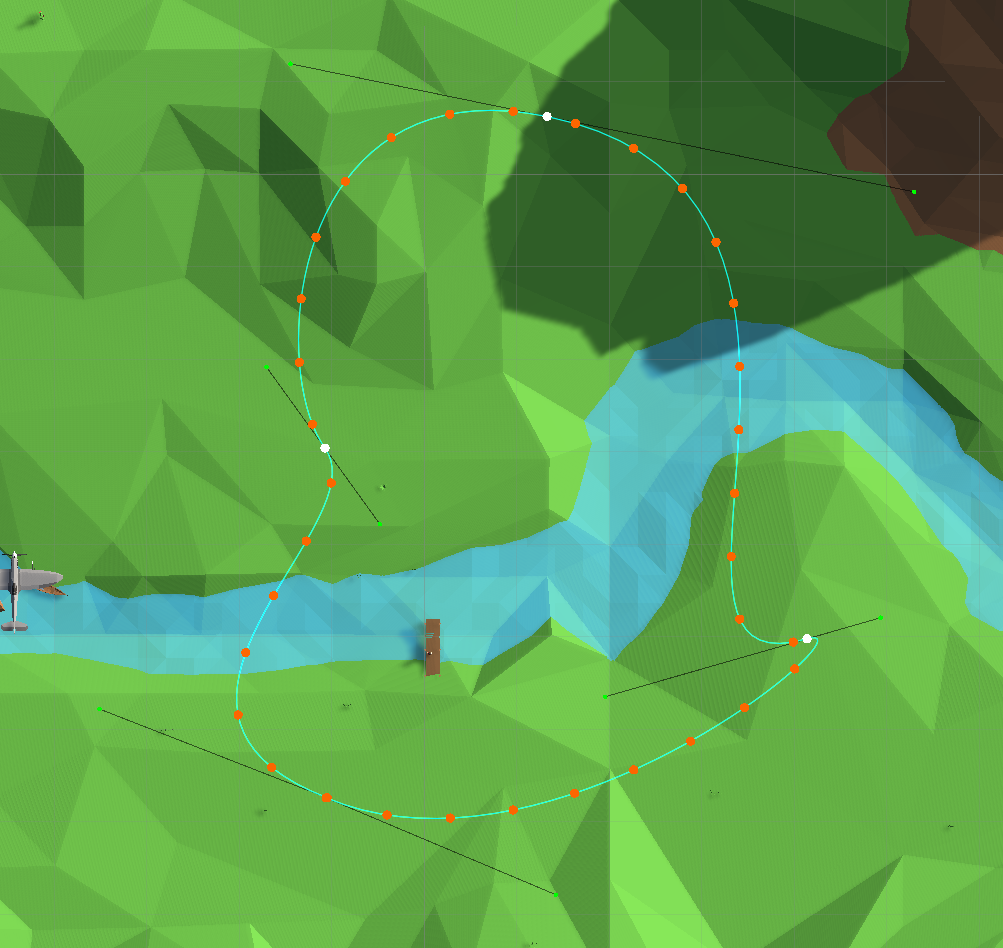
Puntos distribuidos uniformemente a lo largo del camino

Ahora el plano se mueve uniformemente

Así, hemos considerado varias formas de parametrizar el spline relativo a la distancia recorrida, en el artículo que utilicé como fuente, como opción, el autor propone resolver la ecuación diferencial numéricamente, pero, según su propio comentario, prefiere el método modificado Newton:

Prefiero el enfoque del método de Newton porque generalmente t se puede calcular más rápido que con los solucionadores de ecuaciones diferenciales.

Como conclusión, daré una tabla de tiempo para calcular la posición de un punto en la curva que se muestra en las capturas de pantalla en un hilo en un procesador i5-9600K:

Numero de calculos	Tiempo medio, ms
100	0,62
1000	6.24
10000	69.01
100.000	672,81

Creo que esa velocidad de cálculo permite que se utilicen en varios juegos y simulaciones. Estaré encantado de aclarar y criticar en esencia en los comentarios.

Mover un objeto uniformemente a lo largo de una curva

More articles: