Computación cuántica y criptología

El desarrollo de la tecnología informática se está moviendo en varias direcciones, sin limitarse a los fenómenos de la física clásica, la electrónica, la óptica y ahora la mecánica cuántica.

El conocimiento del problema de la criptología cuántica y sus afines cercanos (no solo en las publicaciones) mostró que existen ciertas deficiencias y lagunas en su descripción y presentación. Al describir los detalles de un fenómeno físico en particular, un objeto, el autor ignora su entorno, incluso el más cercano que tiene un impacto directo sobre el objeto (a menudo una influencia perturbadora). Esto no es un reproche a los autores, su derecho a presentarlo como lo presentan. Más bien es mi motivo unirme a la corriente general de conciencia. El lado material de los fenómenos cuánticos se manifiesta de una forma u otra e ignorarlo puede tener un efecto negativo significativo. ¿Qué se quiere decir? Implementación material de computadoras cuánticas (QC), registros, qubits individuales, todos los cuales están hechos de QC. Compartir con los usuarios los resultados obtenidos a través de las redes de comunicación y, finalmente, la protección,la integridad y disponibilidad de tales resultados por parte del intruso también son problemas.

Criptología cuántica y temas relacionados

Una nueva dirección de la física, la información cuántica, surgió en la unión de la mecánica cuántica, la óptica, la teoría y programación de la información, las matemáticas discretas, la física láser, la espectroscopia e incluye cuestiones de sistemas de comunicación cuántica, computación cuántica, computadoras cuánticas, teletransportación cuántica y criptología cuántica, problemas de decoherencia. y espectroscopia de moléculas individuales y centros de impurezas.



Incluso sin tocar la criptología, la física cuántica se basa y utiliza una gran cantidad de fenómenos físicos clásicos para describir sus conceptos y fenómenos, que en la física escolar (y tal vez en la física universitaria) han sido "galopados" o incluso pasados ​​por alto casi todos los conceptos (como familiar) requiere explicación debido a los nuevos descubrimientos y logros de los últimos años, lo que es casi imposible de hacer en el marco del artículo. Pero esta selección de material es problema del autor, no del lector.



En la teoría de la criptología (criptografía + análisis criptográfico), también se pueden distinguir varios períodos (etapas) de desarrollo. Criptología simétrica antigua (clave única, ambos lados del canal de comunicación usan la misma clave); criptología asimétrica o de dos claves (un mensaje se cifra con una clave pública y se descifra con otra, con una privada). Finalmente,

la siguiente etapa en el desarrollo de la criptología cubre el presente y comenzó con la realización de la posibilidad de construir una computadora cuántica (QC) y la criptología cuántica.



Los expertos en criptología clásica entendieron y reconocieron que dicha computadora es una herramienta poderosa para el análisis criptográfico de cifrados, que en cuestión de segundos podrá descifrar un cifrado clásico de cualquier fuerza. Pero vieron el otro lado (positivo) de las posibilidades de apertura: la posibilidad de construir criptografía cuántica con cifrados prácticamente irrompibles.



La idea de la criptografía cuántica nació casi simultáneamente con la idea de utilizar objetos cuánticos para cálculos, es decir, con la idea de crear una computadora cuántica y un sistema de comunicación que utilice canales cuánticos junto con los tradicionales.

El canal cuántico del sistema de comunicación y sus elementos.

Hoy ya vivimos en un mundo de redes cuánticas que se extienden por miles de kilómetros y salen al espacio. El mercado global de sistemas comerciales de comunicación cuántica está dominado por tres empresas: la china Qasky y QuantumCTek, así como la suiza ID Quantique (desde 2001). Suministran prácticamente todo el espectro de soluciones y componentes, desde detectores y fuentes de fotones únicos, generadores de números aleatorios cuánticos hasta dispositivos integrados. En Rusia, dicha red conectó dos oficinas de Gazprombank en 2016, ubicadas a una distancia de unos 30 kilómetros entre sí. Ese mismo año, la República Popular China lanzó el satélite QUESS - Experimentos cuánticos a escala espacial, que proporcionó una distribución cuántica de claves a una distancia de más de 7600 km entre los observatorios de Beijing y Viena.

Esquema de canales de comunicación cuántica

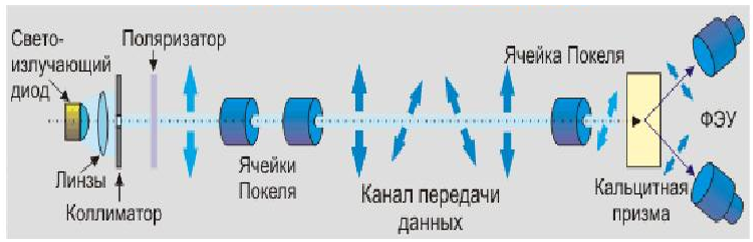
Figura 1. Diagrama esquemático de un canal cuántico y un protocolo de distribución de claves cuánticas



La idea y la implementación de la criptografía cuántica se ilustra en la Figura 1. En la imagen de la izquierda, el lado de envío del mensaje, a la derecha, el lado de recepción. Los elementos necesarios importantes del sistema son los fotomultiplicadores, que desempeñan el papel de fotodetectores, células de Pockels (Pockel), un prisma de calcita (Wollaston) y un polarizador. Eso sí, sin el resto de elementos: un diodo emisor de luz basado en un punto cuántico (láser), lentes, un colimador, fibra óptica y flujo de fotones, el sistema no se puede construir, pero estos elementos son bien conocidos, se han utilizado durante mucho tiempo y en muchos sistemas con fines completamente diferentes. Se implementa un canal cuántico con satélites sin fibra óptica.



Hagamos explicaciones para los elementos individuales del circuito.



El fotón es una partícula elemental, un cuanto de radiación electromagnética en forma de ondas electromagnéticas transversales y un portador de interacción electromagnética. Es una partícula sin masa que puede existir en el vacío solo moviéndose a la velocidad de la luz. La carga eléctrica del fotón también es cero. Un fotón solo puede estar en dos estados de giro con una proyección de giro en la dirección del movimiento (helicidad) ± 1. Muon es el cuanto del campo de muones. El fotón es un cuanto del campo electromagnético. En física, los fotones se indican con la letra γ.



Diodo emisor de luz. En 2001, Andrew Shields y sus colegas de TREL y la Universidad de Cambridge crearon un diodo capaz de emitir fotones individuales. Esto hizo posible transmitir fotones polarizados a largas distancias. La demostración experimental pudo transmitir datos cifrados a una velocidad de 75 Kbps, mientras que más de la mitad de los fotones se perdieron.



La celda de Pockels (a veces llamada celda de Pockel) es un cristal colocado entre dos nicol cruzados. Nicoli no transmite luz en ausencia de un campo eléctrico, y cuando se aplica el campo, aparece la transmisión. El campo externo (líneas de fuerza) puede ser perpendicular a la propagación de la luz (modulador transversal) o paralelo (modulador longitudinal).



El efecto Pockels (el efecto lleva el nombre de F. Pockels, quien estudió este fenómeno en 1893) es el fenómeno de un cambio en el índice de refracción de la luz en los cristales (medios ópticos) cuando se expone a un campo eléctrico constante o alterno. Se diferencia del efecto Kerr en que es lineal en el campo, mientras que el efecto Kerr es cuadrático. El efecto Pockels se observa solo en cristales que no tienen centro de simetría: debido a la linealidad, cuando cambia la dirección del campo, el efecto debe cambiar de signo, lo cual es imposible en cuerpos centralmente simétricos.



El efecto se ve claramente en cristales de niobato de litio o arseniuro de galio.

El efecto Pockels, como el efecto Kerr, es prácticamente inercial (la velocidad es de aproximadamente ^10-10desde). Debido a esto, encuentra un uso activo en la creación de moduladores ópticos. La implementación práctica del efecto se lleva a cabo mediante células de Pockels.



Un punto cuántico (QD) es una pieza en miniatura de material semiconductor de 15 nm de diámetro y 5 nanómetros (nm) de grosor que, cuando se le aplica una corriente, puede capturar solo un par de electrones y huecos.



Hay dos métodos principales para crear puntos cuánticos:

1. La epitaxia es un método para hacer crecer cristales en la superficie de un sustrato:
   
   
   
   
   • epitaxia de haces y haces moleculares;
   • epitaxia en fase gaseosa;
2. síntesis en coloide, en el que las sustancias se mezclan en solución.

La síntesis coloidal se puede utilizar para obtener nanocristales recubiertos con una capa de moléculas tensioactivas adsorbidas. Por tanto, son solubles en disolventes orgánicos, después de la modificación, también en disolventes polares.



Principalmente, los compuestos se cultivan a partir de grupos de elementos III (Ga, Al, In) y V (As, P, Sb) de la tabla periódica; los grupos se denominan AIII BV (o A ₃ , B ₅ ). Los láseres semiconductores y los transistores de microondas se han creado sobre la base de tales QD.



De particular interés son los puntos cuánticos fluorescentes obtenidos por síntesis coloidal, por ejemplo, los puntos cuánticos basados ​​en calcogenuros de cadmio, según su tamaño, fluorescen en diferentes colores. El fenómeno es familiar en la práctica incluso para los niños, ya que se utiliza mucho en los teléfonos móviles.



Propiedades fisicoquímicas de los puntos cuánticos



Amplio espectro de absorción, que permite excitar nanocristales de diferentes colores con una sola fuente de radiación. Un pico de fluorescencia angosto y simétrico (sin una "cola" en la región roja, como en los tintes orgánicos, la mitad del ancho del pico de fluorescencia es de 25 a 40 nm), que proporciona un color puro: puntos de 2 nm - azul, 3 nm - verde, 6 nm - rojo.

Alto brillo de fluorescencia (rendimiento cuántico> 50%). Alta fotoestabilidad.



Funcionamiento de un canal (sistema) de comunicación cuántica. Los fotones individuales del diodo emisor de luz son enfocados por una lente y pasan a través del colimador, después de lo cual ingresan al dispositivo de polarización, donde se polarizan al tipo requerido (uno de 4 (|, -, \, /)) usando una clave de cifrado. Los fotones se mueven, manteniendo la polarización, a lo largo del canal del sistema de comunicación y en el lado receptor pasan nuevamente por la celda de Pockels, luego de lo cual caen sobre un prisma de calcita (Wollaston), que divide un solo flujo de fotones en dos, dirigiendo cada uno a su propio PMT. Este último, utilizando la clave de cifrado, lee la información y la convierte en un mensaje para el destinatario.

Requisitos previos para la computación cuántica

La idea de la computación cuántica fue expresada en 1980 por Yu I. Manin [1] y en 1982 en un artículo de R. Feynman [2]. La aparición de la mecánica cuántica, en cuyo marco se obtuvieron resultados, inexplicables por la mecánica clásica, fue el impulso para el desarrollo no solo de la física, sino también de otras áreas científicas, como la comunicación cuántica, la computación y la criptología.

Para la conveniencia de describir conceptos y fenómenos cuánticos en la computación y manipulación de variables por analogía con un bit binario digital (dígitos binarios = bit), se introduce el concepto de bit cuántico: un qubit.



También se nombran varios modelos físicos de computación cuántica: trampas de iones, qubits fotónicos, qubits topológicos, etc.



Definición... Un qubit es la información más pequeña almacenada en una computadora cuántica. De acuerdo con las leyes de la mecánica cuántica, un qubit puede estar simultáneamente en dos estados propios, denotados | 0⟩ y | 1⟩.



Un qubit puede ser cualquier sistema cuántico de dos niveles, por ejemplo, una partícula cuántica con spin ± ½ en un campo magnético constante (electrón, núcleo, fotón). En este caso, el estado del qubit se puede especificar mediante la superposición A | 0⟩ + B | 1⟩, donde A y B son números complejos que satisfacen la condición | A | ² + | B | ² = 1, es decir la partícula pasa a uno de los estados propios con probabilidades de transición | A | ² en 0 y | B | ² en 1. La técnica de computación con qubits se da con suficiente detalle ( aquí )



Las amplitudes de las probabilidades se describen mediante las fórmulas: A = cos (½θ); B = -e ^iφ sin⁡ (½θ).

Construcción de Qubit. El control de calidad se puede crear utilizando tecnología de circuito integrado plano de silicio nanométrico. En este caso, se deben cumplir los requisitos para aislar qubits de cualquier grado de libertad que conduzca a la decoherencia. Si consideramos los qubits como espines en un donante en un semiconductor, entonces los espines nucleares en la matriz representan un gran depósito con el que pueden interactuar los espines del donante.



Los espines en la matriz deben estar en el estado I = 0. Este importante requisito excluye todos los semiconductores de los tipos AIII BV para la síntesis de matrices, ya que solo el silicio es un isótopo estable ²⁸Si con giro I = 0. Otro requisito es el enfriamiento profundo, la temperatura debe ser tan baja que se excluya la ionización del donante. Un requisito importante en el caso de considerar dos o más qubits es el requisito de superposición de las regiones de las funciones de onda cuánticas de Schrödinger.



El donante de Si (silicio) con spin I = ½ es un solo átomo de ³¹ P (fósforo). Para el sistema ²⁸ Si: ³¹ P en T = 1,5 K y una concentración baja de ³¹ P, el tiempo de relajación del espín del electrón es de aproximadamente 1000 segundos y el tiempo de relajación del espín nuclear es de ³¹P supera las 10 horas. Los cálculos cuánticos son posibles para espines nucleares cuando se localizan en un donante cargado positivamente en una matriz de semiconductores. Su temperatura debe ser lo suficientemente baja (3-5 milikelvin), a la que se excluye la ionización del donante.



El estado de un fotón no se puede leer (medir) dos veces. Se notará un intento de "interceptar" el mensaje. Al identificar (medir) el estado actual de un qubit {| 0⟩ o | 1⟩}, los estados deben ser físicamente distinguibles y estimados por probabilidades. Estas probabilidades sirven indirectamente para estimar el estado inicial (antes de la medición) del qubit. Los qubits pueden verse como vectores unitarios en un espacio vectorial complejo bidimensional con una base fija ortogonal {| 0⟩} y {| 1⟩}. La teoría cuántica de campos considera las partículas como oscilaciones (cuantos) de campos. El fotón es un cuanto del campo electromagnético. Muon es muónico.



Una superposición de estados es algo así como una lista de todos los estados posibles de un objeto cuántico (digamos un fotón). Antes de que se midiera. No es una onda ni una partícula, sino algo más que tiene propiedades similares: "ondulación, onda".

Cuando se consideran varios qubits (registro de qubits) simultáneamente, un cambio en el estado de uno de los qubits conduce a un cambio en el estado de otros. Cambian de acuerdo con el primero.



Esta relación se llama entrelazamiento de estados y el conjunto de qubits se interpreta como un registro cuántico lleno de una computadora cuántica. Este registro puede estar en varios estados e implementar intercambio y dependencias físicas sutiles entre qubits.



Requisitos para CC



Los requisitos y condiciones generales para crear un CC de estado sólido también se formulan:

• «» ( );
• (100…1000Å) , , ;
• , (- );
• , () , ;
• , , ∆ = µgB, ∆N = =µNgNB, – , µ, µN – ; gN, g – g – ;
• () ;
• ( ), ;
• - - n- ;
• «» , , , , , CNOT π⁄8. .

Requisitos para el procesamiento de información cuántica y su transmisión (intercambio):



a) El sistema debe tener la capacidad de convertir de manera confiable los datos almacenados en forma de qubits estacionarios (computacionales) en qubits de red (transmitidos) (por ejemplo, fotones) y viceversa.



b) El sistema debe poder transferir correctamente qubits de red entre puntos finales.

Creación de QC y sus elementos

Las computadoras cuánticas se están desarrollando a un ritmo rápido. Los QC se crean según varios principios diferentes: RMN - resonancia magnética nuclear, ESR - resonancia de espín de electrones, espín nuclear en silicio. Una partícula que genera un qubit puede ser un electrón, un núcleo, un fotón, capaz de cambiar el estado de giro.



Una computadora cuántica (QC) es un dispositivo de estado sólido (semiconductor) que utiliza fenómenos físicos cuánticos y las propiedades de los espines electrónicos (nucleares) para realizar cálculos en la resolución de problemas.



Hay muchas plataformas sobre las que construir una computadora cuántica universal. Sin embargo, cada enfoque tiene sus inconvenientes. Por ejemplo, los qubits superconductores tienen tiempos de coherencia cortos en comparación con otras realizaciones, y es difícil construir una computadora cuántica grande a partir de átomos fríos.

Los puntos cuánticos son una implementación prometedora de los qubits, pero también tienen muchos problemas. Uno de ellos es una medida cualitativa de qubits, que no destruye el estado cuántico del sistema. En este contexto, los electrones individuales en puntos cuánticos se consideran qubits, y los estados 0 y 1 se describen mediante el espín del electrón.

Una computadora cuántica sobre espines nucleares en silicio

Los desarrolladores de QC tenían algo en lo que basarse en sus actividades. La tecnología de circuitos integrados planos de silicio a nanoescala funciona, se enumeran los requisitos funcionales, las limitaciones y las condiciones se definen en su mayoría. El sistema Si: ³¹ P se estudió exhaustivamente hace unos 60 años en experimentos de doble resonancia electrón-nuclear.





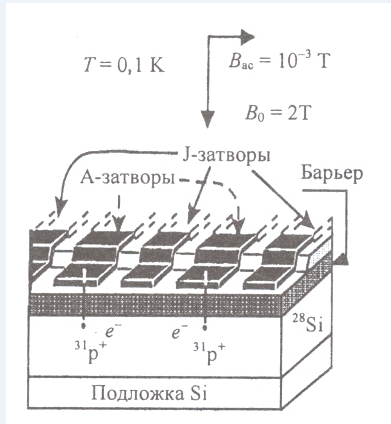
Figura A - Dos qubits en un registro unidimensional (dos donantes de ³¹ P con electrones ligados incrustados en ²⁸ Si)



A una concentración baja de ³¹ P y a T = 1,5 K, el tiempo de relajación del espín del electrón es de aproximadamente 1000 s, y el tiempo de relajación del espín nuclear es de ³¹ P supera las 10 horas. Cuando la temperatura desciende a 0,1 K, excluida la ionización del donante, la función de onda electrónica se concentra en el núcleo donante, lo que conduce a una interacción hiperfina entre los espines del núcleo y el electrón. La placa de silicio se coloca en un campo magnético constante Bo≥2T.



Dos qubits en un registro unidimensional contienen dos donantes de ³¹ P con electrones ligados incrustados en ²⁸Si. Están separados de las puertas metálicas de control en la superficie por una capa de SiO ₂ . A - los electrodos controlan (establecen) la frecuencia de resonancia del qubit de espín nuclear; Las puertas J controlan la interacción de los electrones de los espines nucleares vecinos.

Computadora cuántica de resonancia de espín electrónico

Cuando se usa ESD, la pureza del isótopo de la matriz de silicio no es crítica. Para una serie de indicadores, la ESR es preferible al espín nuclear, un campo magnético de 2 T (Tesla) proporciona una frecuencia de ESR de 56 GHz y, debido a la alta energía Zeeman, los espines de electrones permiten la operación hasta frecuencias en el rango de gigahercios. Los espines nucleares son solo hasta 75 kHz. En T = 1 K, los espines de los electrones (a diferencia de los nucleares) están completamente polarizados. En lugar de silicio, se utilizan heteroestructuras de Si / Ge, lo que permite controlar la masa efectiva del electrón donante. Las puertas J de las células son innecesarias. Para las mediciones (leer los resultados), no se pueden usar transistores de un solo electrón, sino transistores de efecto de campo ordinarios a bajas temperaturas.





Figura B - Ilustración del método para detectar el estado de espín de un electrón



Una persona no puede observar directamente los estados de qubits y registros cuánticos. Cuando se aplica voltaje a los dos electrones y la espalda antiparalela puerta (estado singlete) (izquierda y derecha) están asociados con uno y el mismo donante (D ^- estado) .They puede ejecutar transiciones en un nuevo estado, que produce una corriente eléctrica que medido con un dispositivo capacitivo (transistor de un solo electrón). Esto asegura la determinación del estado de espín del electrón y del núcleo donante ³¹ P. En este caso, se realiza el principio de Pauli.





Figura C - Esquema de la interacción de intercambio entre dos qubits (operación de dos qubits)



Con un aumento en el voltaje de la puerta, la energía de enlace disminuye y el radio de Bohr de los donantes similares al hidrógeno aumenta. En el plano xy, los electrones pueden ser atraídos electrostáticamente a una de las barreras formadas por capas B de la composición Si _0.23 Ge _0.77 . El potencial de Coulomb disminuye V = -q / √ (r ² + d ² ), donde r ² = x ² + y ² es el cuadrado de la distancia horizontal desde el donante y d es la distancia vertical desde la barrera hasta el donante.

En este caso, la energía de la unión de Coulomb de los electrones disminuye y aumenta la superposición de sus funciones de onda, lo que permite realizar operaciones de dos qubits.



Diseño ESD de un qubit

Consideraremos la estructura de la celda de registro KK para dos qubits. La celda de material ESD se crea cultivando una solución sólida de Si / Ge sobre una base de silicio (cristal), sobre la cual se cultivan secuencialmente 5 capas de trabajo más.





Figura E - La estructura de la celda ESR para dos qubits



Izquierda (a) - el perfil de energía de la heteroestructura Ge _{1 - x} Si _x ; a la derecha (b) - sección transversal de una celda de dos qubit. PT - transistores de efecto de campo; <111> - orientación del sustrato.



Las capas principales son T (tuning) "tuning" y D2-donor sin cortes de bandas de conducción, donde se realizan cálculos cuánticos (entre átomos 2000 Å). El espesor y la composición de las capas están determinados por el diagrama de energía (izquierda) y los requisitos para la acción de las puertas de control (encima de las capas). Las capas T y D2 están encerradas entre las capas de barrera (su grosor es de 200 Å), que prohíben que los electrones se muevan verticalmente, difieren en composición y tienen un factor g diferente: g (T) = 1,563; g (D2) = 1.995 Los electrones de la capa D2 desempeñan el papel de qubits. Las roturas de banda de conducción iguales a 20 meV implementan la prohibición y conservación de electrones donantes de qubit, tanto portadores como información cuántica.





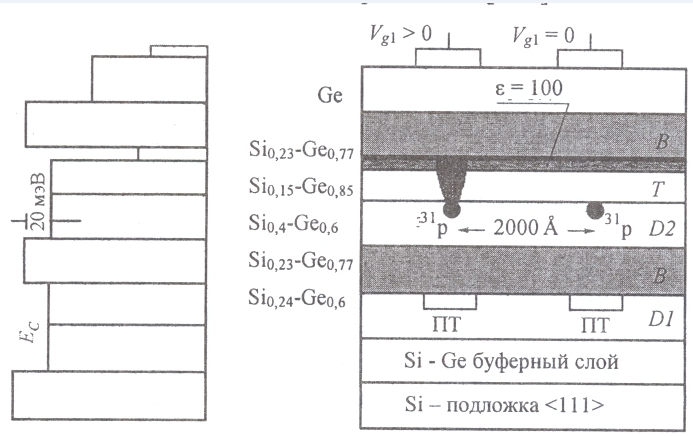
Figura E - Estructura de la celda ESD para dos qubits. Se mantienen las designaciones de la figura anterior



Considere la influencia de la orientación del sustrato de silicio cristalino. La orientación del sustrato, indicada por el símbolo [001] (teoría cristalográfica), ofrece varias ventajas. la energía de la banda de conducción cambia más rápido para esta dirección; las composiciones sólidas con voltajes más bajos se pueden seleccionar a una altura de barrera de aproximadamente 50 meV, que es más del doble de aumento en comparación con la orientación [111].



En consecuencia, las capas de barrera, manteniendo la misma probabilidad de tunelización, pueden ser más delgadas (miniaturización), y las tensiones permisibles son mucho mayores. El uso de una capa con parámetros que conducen a un aumento del radio de Bohr y, en consecuencia, a un aumento de la posible distancia entre qubits, condujo al depósito epitaxial de una capa activa con constante dieléctrica más alta. Al aumentar las distancias, la frecuencia de intercambio entre qubits disminuye significativamente.



Para los controles de calidad basados ​​en RMN en átomos de fósforo en silicio, se encontró una solución a un problema bastante complicado en la creación de qubits: la disposición exacta de los átomos donantes (hasta 100 Å)





Figura F - Diagrama del proceso de construcción de un registro a partir de células de RMN de qubits



El diagrama de la disposición de los átomos de fósforo individuales en el silicio se ha vuelto realizable gracias a los avances en nanotecnología. La superficie de la oblea de silicio (Si 2 x 1) limpia en condiciones de vacío ultra alto se pasiva con una monocapa de hidrógeno. Luego, de acuerdo con un programa especial, con la ayuda de una sonda de microscopio de efecto túnel, los átomos de hidrógeno individuales se desorben en lugares específicos. Después de eso, se introduce vapor de fosfina en la cámara a una presión de 10 ^-8 mm Hg. Arte. Las moléculas de fosfina adsorbidas luego se disocian a una temperatura de 500 ° C, dejando los átomos de fósforo unidos al silicio en los sitios de adsorción. Después de eso, se realiza un crecimiento excesivo de silicio a baja temperatura de la estructura resultante.



Es posible crear una computadora capaz de computación en paralelo al nivel de todo el dispositivo de computación.



Enumeremos los factores y hechos que aumentaron el interés en el control de calidad y los incentivos para su desarrollo práctico.



Se han creado algoritmos para computadoras cuánticas que resuelven problemas difíciles:

• búsqueda de elementos (fuerza bruta) en una base de datos no estructurada 1996 (LK Grover);
• modelar la evolución de los sistemas cuánticos, por ejemplo, reacciones nucleares;
• Problema de factorización de números grandes (ZFBCH) 1994 (PW Shor);
• cálculo del logaritmo discreto (DLOG) en un campo finito, en una curva elíptica;
• y etc.

Se ha desarrollado un procedimiento para controlar los estados cuánticos (corregir errores cuánticos).



Se ha realizado un experimento que implementa la computación cuántica para el algoritmo de Grover y otros en QC de resonancia magnética nuclear líquida.



Sobre la base de elementos de estado sólido, se crearon variantes de estructuras CC:

• basado en puntos cuánticos (D. Loss, G. Burkard, L. Fedichkin, K. Valiev);
• basado en uniones Josephson superconductoras (DE Averin);
• en los espines nucleares de ³¹ átomos de fósforo donantes de P en ²⁸ Si isotópicamente puro (BEKane).
• en los espines de electrones de los mismos átomos de fósforo en heteroestructuras epitaxiales
• Ge1-x Seis (D. DiVincenzo).

A continuación se muestran fórmulas para estimar los estados de un qubit y sus probabilidades.

Un estado cuántico es cualquier estado posible en el que puede estar un sistema cuántico. Un estado cuántico puro se puede describir: 1) en mecánica de ondas: una función de onda; 2) en mecánica matricial, por un vector.



Las computadoras cuánticas prometen cambiar mucho en nuestro mundo. Por su propia naturaleza, se adaptan bien a los cálculos necesarios para invertir funciones unidireccionales. Para la criptografía simétrica, esto no es tan malo. El algoritmo de Grover muestra que una computadora cuántica acelera los ataques tanto que la longitud efectiva de la clave se reduce a la mitad. Es decir, una clave de 256 bits es tan compleja para una computadora cuántica como una clave de 128 bits para una computadora normal: ambas son seguras en el futuro previsible.



Para la criptografía de clave pública, la situación es más grave. El algoritmo de Shor rompe fácilmente todos los algoritmos populares de clave pública basados ​​tanto en la factorización como en el logaritmo discreto. Duplicar la longitud de la clave aumenta la dificultad de descifrar ocho veces. Esto no es suficiente para un funcionamiento estable (el mecanismo de corrección de errores en una computadora cuántica puede convertirse fácilmente en un problema insuperable para ellos).



Cifrado de clave pública (utilizado principalmente para el intercambio de claves)

La palabra clave aquí es "intercambio de claves" o, como suele decirse, acuerdo de claves. Y el cifrado en sí (AES, "Grasshopper", "Magma", etc.) se realiza en claves simétricas (por supuesto, con un cambio de clave periódico, todo tipo de keymeching-b, tal vez incluso generación para cada paquete). Se trata solo de la clave de cifrado.



En física cuántica (mecánica), hay una serie de principios que están ausentes en la física clásica tradicional.



Principio de incertidumbre de Heisenberg, es imposible obtener simultáneamente las coordenadas y el momento de una partícula, es imposible medir un parámetro de un fotón sin distorsionar otro.

El principio de exclusión de Pauli establece que dos electrones (o cualesquiera otros dos fermiones) no pueden tener el mismo estado mecánico cuántico en un átomo o una molécula.



En otras palabras, ningún par de electrones en un átomo puede tener los mismos números cuánticos de electrones. El principio prohíbe la clonación (copia) de qubits.

La clonación es una operación en un par o más de qubits, como resultado de lo cual se crea un estado que es un producto tensorial de estados idénticos de subsistemas.



El teorema de la prohibición de la clonación (copia) es una afirmación de la teoría cuántica de que es imposible crear una copia ideal de un estado cuántico desconocido arbitrario de una partícula. El teorema fue formulado por Wutters, Zurek y Dieck en 1982 y ha sido de inmensa importancia en los campos de la computación cuántica, la teoría de la información cuántica y campos relacionados.



El estado de un sistema cuántico se puede vincular al estado de otro sistema. Por ejemplo, puede crear un estado entrelazado de dos qubits utilizando la transformada de Hadamard de un qubit y la puerta cuántica de hardware de dos qubits C-NOT. El resultado de tal operación no será la clonación, ya que el estado resultante no se puede describir en el lenguaje de los estados del subsistema (el estado no es factorizable).





La pregunta difícil es cómo interpretar el resultado.



Ventajas y desventajas de la comunicación cuántica y CC sobre la clásica.



Aspectos positivos del uso de sistemas cuánticos.

• QC opera en cálculos no con números, sino con estados cuánticos;
• en la física tradicional (clásica), los estados individuales de las partículas se combinan mediante la multiplicación escalar ordinaria de vectores; en este caso, el número posible de estados de n partículas forma un espacio vectorial de dimensión 2 ⁿ ;
• () |0⟩ |1⟩ {|0⟩} {|1⟩}. . n ( n ) 2ⁿ. – {|0⟩ |1⟩} ; – {00, 01, 10, 11} . . ;
• m () 2^m . .
• .

El producto tensorial de los estados es la causa de la paradoja EPR y, hasta cierto punto, una explicación para ella.

Producto tensor

Considere el caso de 2 qubits.





El caso de 2 qubits. Existen 4 variantes de su estado conjunto,



estos 4 vectores en las columnas de la tabla son básicos en el espacio de dos qubits. Formalmente, se describe a continuación. Si hay espacios 1 y 2 con dimensiones d1 y d2 y bases ortonormales {ei} y {fj}, entonces podemos definir un espacio con base {$$$e_i⨂f_j$}, donde i varía de 1 a d1 yj varía de 1 a d2.



Si introducimos el producto escalar en el nuevo espacio según la ley

$$$⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩$

y continuar con los otros vectores, entonces el resultado es un espacio de Hilbert, que se llama el producto tensorial de H1 y H2 y se denota $$$_1⨂ _2$... Evidentemente, su dimensión es d1d2.



Producto tensorial de operadores$$$_1 ϵ S(H_1 )$ y $$$_2 ϵ S(H_2 )$ Es el operador $$$_1⊗_2$ en el espacio $$$_1⨂_2$actuando bajo la ley$$$_1⊗ _2 )|e_1⨂e_2 ⟩=( _1│e_1 ⟩ )⨂( _2│e_2 ⟩$). Surge la pregunta de si algún estado en el espacio$$$_1⨂_2$puede definirse como el producto tensorial de estados pertenecientes a los espacios parciales H1 y H2?



La respuesta a esta pregunta es negativa, y un contraejemplo clásico es el estado en el espacio de dos qubits$$$_1^2 ⨂_2^2$, llamado EPR por las primeras letras de los apellidos de los descubridores (Einstein, Podolsky, Rosen):



$$$|ψ_EPR ⟩= 1/√2 (|00⟩+|11⟩)$...



Es fácil ver que este estado no se puede representar como un producto tensorial de estados de una partícula:



$$$|ψ_EPR ⟩≠(a_1 |0⟩+b_1 |1⟩)⨂(a_2 |0⟩+b_2 |1⟩)$...

Criptología cuántica

La criptografía cuántica (QCG) es un método de seguridad de las comunicaciones basado en los principios de la física cuántica. A diferencia de la criptografía tradicional, que utiliza métodos matemáticos para garantizar la confidencialidad de la información, KKG se centra en los fenómenos físicos, considerando los casos en los que la información se transfiere utilizando objetos de la mecánica cuántica.



Criptoanálisis cuántico (QCA). La generalización y desarrollo de la criptografía cuántica ha provocado la aparición de un contrapeso: el criptoanálisis cuántico, que en algunos casos tiene, según la teoría, ventajas sobre lo habitual. RSA y otros cifrados teóricos de números y métodos criptográficos basados ​​en los problemas de factorizar números grandes, encontrar el logaritmo discreto perderá su fuerza con el advenimiento del QCA cuántico.



Según las leyes de la física, el estado de un cuanto de luz (fotón) no se puede leer dos veces: después de la primera acción sobre el fotón, su estado cambiará y un segundo intento dará un resultado diferente. Se notará un intento de "interceptar" información. Por lo tanto, la criptografía cuántica se considera hoy en día la dirección de cifrado más prometedora.



Para resolver estos problemas, en particular, se desarrolló el algoritmo cuántico de Shor (1994), que permite encontrar en un tiempo finito y aceptable todos los factores primos de números grandes o resolver el problema del logaritmo y, como consecuencia, romper los cifrados RSA y ECC. Por lo tanto, construir un sistema criptoanalítico cuántico lo suficientemente grande es una mala noticia para RSA y algunos otros sistemas asimétricos. Solo es necesario crear una computadora cuántica capaz de ejecutar el algoritmo requerido.



A partir de 2012, las computadoras cuánticas más avanzadas pudieron factorizar el número 15 (en 150 mil intentos se obtuvo la respuesta correcta en la mitad de los casos, de acuerdo con el algoritmo de Shor) y 21.



Protección de la información (mensajes) del acceso no autorizado y de la modificación con El uso de objetos cuánticos fue sugerido en 1970 por Steven Wiesner. Bennett S.N. y J. Brassard, 10 años más tarde, propusieron usar estos objetos para transferir claves de cifrado en forma de protocolos de distribución de claves cuánticas: BB84 y, posteriormente, en 1991 y 1992, un protocolo mejorado.



La criptografía cuántica, junto con sus ventajas y beneficios, se caracteriza por ciertas limitaciones y aspectos negativos. Como en cualquier sistema de comunicación en un sistema de comunicación que utiliza criptografía cuántica, existen nodos con equipos de recepción y transmisión de usuario, canales de comunicación, fuentes de energía, etc.



Los aspectos negativos de la comunicación cuántica que se señalan suelen ser los siguientes.



Los equipos complejos deben instalarse en ambos lados (transmisión y recepción) de un canal de un sistema de comunicación cuántica:

• imperfección de fuentes de fotones individuales (tasa de generación baja);
• el sistema de control de polarización de fotones está mal protegido contra interferencias;
• imperfección de los receptores de fotones individuales, los detectores sensibles funcionan además de los fotones y otras partículas;
• , ; ;
• 100 ( 100 ) , ( , , );
• ;
• ( $81000).

Para medir el ángulo de polarización de los fotones, necesita saber exactamente cómo está orientado el equipo en ambos extremos del canal. Estas condiciones limitan la propagación de la criptografía cuántica a los dispositivos móviles.



Con el tiempo, se encontró una opción aceptable. Un solo usuario puede instalar equipos complejos en un extremo del canal. Otro usuario acepta una señal y solo modifica el estado de los fotones, agregando su información a los estados cambiados. Los fotones cambiados se devuelven. Dicho equipo ya puede caber en un dispositivo de bolsillo.



Con respecto a establecer la orientación de los equipos, se propone realizar mediciones en direcciones aleatorias, y su lista debe publicarse abiertamente. Para trabajo legítimo y descifrado, use solo direcciones que coincidan con los suscriptores. El método se denomina "distribución de clave cuántica independiente del marco de referencia".

Distribución de claves cuánticas

La distribución de claves cuánticas (QKD) es un método de transferencia de claves que utiliza fenómenos cuánticos para garantizar comunicaciones seguras. Este método permite que dos partes, conectadas a través de un canal de comunicación abierto de fibra óptica o redes libres, transmitan un flujo de fotones, creen una clave aleatoria común, que solo ellos conocen, y la utilicen para cifrar y descifrar mensajes.



El objetivo principal de los protocolos conocidos de distribución de claves cuánticas (QKD) es hacer coincidir secuencias de partículas transmitidas al azar (fotones).

En 1935, Einstein y un grupo de personas de ideas afines, tratando de desafiar la interpretación de Copenhague de la mecánica cuántica, formularon una paradoja, más tarde llamada paradoja de Einstein-Podolsky-Rosen (la paradoja de EPR no describe todos los estados de qubit mediante métodos de tensor).



Entre los posibles QKD, los primeros BB84, B92 (Bennett), B91 (Eckert, otro nombre de EPR), posteriormente CW (variables continuas), el protocolo suizo COW (cifrado unidireccional coherente de una vía coherente), Lo05 (creado por Lo H.-K. Ma K. y Chen K. 2005), SARG, Decoy State, DPS (diferencial Phase Shift), con estado de referencia, fase-tiempo.

Algoritmo de Charles H. Bennett. Algunos de los protocolos enumerados se analizan en detalle a continuación.

Protocolo cuántico BB84

Ejemplo 1 . Implementación de la distribución de claves de cifrado cuántico (protocolo BB84), que utiliza estados ortogonales de objetos cuánticos. El receptor del mensaje actúa sobre los objetos (fotones), eligiendo aleatoriamente el tipo de medida: cambia la polarización lineal del fotón (|, -), o la diagonal (\, /)



IMPLEMENTACIÓN DEL PROTOCOLO CUÁNTICO BB84





Protocolos Lo05 y E91 . Este protocolo fue desarrollado por Arthur Eckert en 1991. También tiene el nombre EPR (Einstein-Podolsky-Rosen) ya que se basa en la paradoja de Einstein-Podolsky-Rosen. Lo05 es un protocolo de distribución de claves criptográficas cuánticas creado por los científicos de Luo H.-K. Ma K. y Chen K. Quantum Key Distribution (QKD) permite que dos usuarios, un remitente y un receptor, se comuniquen con absoluta seguridad en presencia de un intruso.



En 1991, Bennett sugirió usar el siguiente algoritmo para registrar cambios en los datos transmitidos usando transformaciones cuánticas:

1. El remitente y el receptor acuerdan una permutación arbitraria de bits en las cadenas para hacer que las posiciones de error sean aleatorias.
2. k (k , ).
3. . .
4. , , .
5. , , k.

Para determinar si quedan o no errores no detectados, el receptor y el emisor repiten comprobaciones pseudoaleatorias, a saber: el receptor y el emisor anuncian abiertamente la mezcla aleatoria de las posiciones de la mitad de los bits en sus cadenas; el receptor y el emisor comparan abiertamente las paridades (si las cadenas difieren, las paridades no deben coincidir con probabilidad 1/2); si hay una diferencia, el receptor y el remitente utilizan la búsqueda binaria y la eliminación de bits no válidos.



Si no hay diferencias, después de m iteraciones, el receptor y el emisor reciben líneas idénticas con una probabilidad de error de 2 ^{- m} .



Protocolo cuántico B92Es uno de los primeros protocolos para la distribución de claves cuánticas, que fue propuesto en 1992. C. Bennett. De ahí el nombre B92, por el que hoy se conoce este protocolo. El protocolo B92 se basa en el principio de incertidumbre, a diferencia de protocolos como el E91. Los portadores de información son sistemas de 2 niveles llamados qubits. Una característica importante del protocolo es el uso de dos estados cuánticos no ortogonales.





Ejemplo 2 . Implementación de la distribución cuántica de la clave de cifrado (protocolo B92), que utiliza estados cuánticos ortogonales y no ortogonales (polarizaciones de fotones).





1. En el caso de una implementación de EPR, el remitente elige aleatoriamente una base para medir el estado de un fotón de un par correlacionado con EPR, ya sea lineal o circular.



2. En el segundo paso, las acciones del remitente dependen de la versión del protocolo.



a) para la implementación de EPR, selecciona una secuencia aleatoria de bases para medir la polarización de fotones;



b) El emisor selecciona una secuencia aleatoria de fotones polarizados y los envía al receptor.



3. El receptor mide las polarizaciones de los fotones que llegan usando una secuencia de bases aleatorias.



4. Los resultados de las mediciones del receptor (fuente no ideal, canal de comunicación y detector conducen a la pérdida de fotones).



5. El receptor informa al remitente de la base para medir la polarización de cada fotón recibido.



6. El remitente informa al destinatario qué bases fueron seleccionadas correctamente por el destinatario.



7. El emisor y el receptor almacenan los datos de fotones medidos en las polarizaciones correctas y descartan todos los demás.



8. El resto de los datos se interpretan de acuerdo con la tabla de códigos:



9. El remitente y el receptor comparan sus claves con la paridad del subconjunto de bits seleccionado. Si al menos un bit es diferente, dicha verificación muestra la existencia de un intruso escuchando en el canal.



10. Los lados descartan uno de los bits del subconjunto seleccionado.

Como resultado de la comunicación utilizando el protocolo B92, el remitente y el receptor reciben una clave secreta compartida 0101101 y revelan la ausencia de un intruso con una probabilidad de 1/2.

Protocolo de Quantum COW

Ejemplo 3 . Implementación de la distribución de claves de cifrado cuántico (protocolo COW), que utiliza cifrado unidireccional coherente.



El emisor envía "0" con probabilidad (1 - f) / 2, "1" con probabilidad (1 - f) / 2 y estados de control (señuelo) con probabilidad f.



El receptor anuncia qué bits de la secuencia ha medido en la línea de tiempo y cuando se enciende el detector DM2, devuelve la secuencia al remitente.



El remitente realiza (cribado de clave): le dice al receptor qué bits debe excluir de su clave sin procesar, ya que se deben a la detección de estados de control.



Remitente. Analizando los disparadores en DM2, evalúa las violaciones de coherencia a través de la visibilidad V1−0 y Vd y calcula la información del intruso.



Corrección de errores en curso. Fortalecimiento del secreto de la clave tamizada Un



hecho interesante de "cancelar el colapso" de la función de onda lo dan Korotkov y Jordan.



Le llamaron la atención y realizaron un experimento que prueba y supuestamente confirma la teoría. Pero aparentemente, una sola confirmación no es suficiente y nadie ha publicado ideas o aplicaciones sobre el uso del hecho. Simplemente, no podía dejar de mencionar esto.

Cancelación del colapso por el experimento (2008) del grupo Nadav Katz, que confirma la veracidad de la teoría de Korotkov-Jordan (2006) evitando el colapso por múltiples retornos del estado qubit.

En general, cualquier sistema cuántico está en una superposición de todos sus estados posibles hasta que ocurre una medición y asume uno de los estados posibles. Después de la medición, el sistema asumirá un estado específico (colapso).



Y así, en 2006, Korotkov y Jordan publicaron un artículo titulado "Desglose de la función de onda deshaciendo las mediciones cuánticas", que en ruso se puede traducir aproximadamente como "Cancelar el colapso de la función de onda cancelando la medición cuántica". o arXiv: 0708.0365v1 [Quant-Ph:

Vulnerabilidades criptoanalíticas, ataques, su clasificación

Los expertos creen que la distribución de claves cuánticas no es invulnerable a la piratería, pero sí bastante accesible para un intruso. Otra cosa es que se pueden detectar las acciones del intruso, y la llave no es necesaria y se reemplaza por otra. Las implementaciones específicas de tales sistemas permiten un ataque exitoso y roban la clave generada.



Es posible una lista bastante extensa de ataques.



Ataques a equipos de un sistema cuántico:

• uso de un divisor de haz;
• utilizando un pulso potente (fotodetectores de avalancha cegadores);
• uso del espectro de fuentes de fotones, si difieren;
• el uso por parte del infractor de un PRNG similar al del remitente.

Ataques al estado de cuantos (fotones):

• usando coherencia;
• los ataques coherentes consideran tácticas de relevo;
• ataques incoherentes: interceptor de retransmisión; usando clonación de fotones;
• - ataques combinados:
  
  
  
  - interacción con qubits individuales;
  
  - medidas de sus matrices.

Tres ejemplos de ataques implementados (de publicaciones en la red)

Ataque del divisor de haz en VACA

Se supone que los recursos del intruso son ilimitados. Ataques a protocolos de distribución de claves: un esquema general para preparar y medir estados cuánticos, un procedimiento para obtener los resultados de las mediciones de estados cuánticos de una clave en los lados del emisor y del receptor. Ataques a la implementación técnica de sistemas criptográficos cuánticos (hacking cuántico).

• Atenuación ⇒ µB = 10 - δl / 10µ;
• Divisor de haz + canal de comunicación ideal;
• µ máx E = µ - µB = (1 - 10 - δl / 10) µ.

En la edición de febrero de la revista "Quantum Electronics" (entre los fundadores, los principales institutos de física de la Academia de Ciencias de Rusia), se describe un método: cómo leer un mensaje transmitido a través de una red de comunicación cuántica, implementado utilizando tecnología suiza, y pasar desapercibido. Como está escrito en el artículo, “la idea principal del ataque es medir individualmente una parte de los estados interceptados y enviar el resto sin cambios. Los autores han calculado los valores óptimos de los parámetros de ataque para una longitud arbitraria del canal de comunicación ".



El desarrollo ruso tiene un mayor potencial de protección para la creación de redes multiusuario debido a una forma especial de transmitir varios canales en una línea. Esto le permite aumentar significativamente la velocidad o el ancho de banda del canal cuántico, cree el desarrollador.



Otro ejemplo es el ataque PNS (Photon number splitting attack) [1], realizado por físicos de Australia y Japón, quienes por primera vez realizaron una medición cuántica no destructiva de un qubit, que consistía en un electrón en un punto cuántico. Los científicos han demostrado que la fiabilidad de tal medición es superior al 99,6 por ciento. El artículo fue publicado en Nature Communications.



Científicos de Australia y Japón, dirigidos por el profesor Seigo Tarucha del Centro de Ciencias RIKEN, propusieron medir un qubit en un punto cuántico utilizando otro electrón entrelazado con un qubit. Tal implementación permite conservar el estado del qubit de trabajo durante mucho tiempo, lo cual es necesario, por ejemplo, para la implementación de códigos de corrección de errores.



Para probar la lectura no destructiva, los físicos colocaron dos electrones en puntos cuánticos de Si / SiGe: uno de los electrones se usó como un qubit de trabajo y el otro como ancilla para la medición. Los científicos controlaron la conexión de los qubits con un campo magnético creado por un microimán en un chip.







Un diagrama de la implementación física de dos qubits, que representa dos electrones que los científicos han colocado en puntos cuánticos. J. Yoneda y col. - Nature Communications 11, 1144 (2020)



Literatura:



D.A. Kronberg, Yu.I. Ozhigov, A.Yu. Chernyavsky. Criptografía cuántica. - 5ta ed. - Prensa MAKS, 2011 .-- S. 94-100. - 111 p. Archivado el 30 de noviembre de 2016

Bennett CH, Brassard G. Criptografía cuántica: distribución de claves públicas y lanzamiento de monedas // Actas de la conferencia internacional sobre computadoras, sistemas y procesamiento de señales, dic. 9-12, 1984, Bangalore, India - IEEE, 1984. - P. 175

Bennett, CH y Brassard, G., Conf. sobre computadoras, sistemas y procesamiento de señales, Bangalore, India, 175-179 (1984).

Criptografía cuántica de Bennett CH utilizando dos estados no ortogonales cualesquiera // Phys. Rdo. Letón. 1992. Vol. 68, 3121.

Ekert AK, Hutter B., Palma GM, Peres A. Escuchas clandestinas sobre sistemas criptográficos cuánticos // Physical Review A. - 1994. - Vol. 2, No. 50. - P. 1047-1056

Einstein A., Podolsky B., Rosen N. ¿Se puede considerar completa la descripción de la mecánica cuántica de la realidad física? // Phys. Rdo. A - 1935. - Vol. 47, 777.

Shor PW Esquema para reducir la decoherencia en la memoria de la computadora cuántica // Phys. Rdo. A 1995. Vol. 52, 2493.

Shor PW Algoritmos de tiempo polinomial para factorización prima y logaritmos discretos en una computadora cuántica // SIAM J. Sci. Statist.Comput. 1997. Vol. 26 de 1484.

Shor PW, Preskill J. Prueba simple de seguridad del protocolo de distribución de claves cuánticas BB84 // Phys. Rdo. Letón. 2000. Vol. 85, 44