En ese momento, no sabía nada sobre el valor p, las pruebas de hipótesis o incluso la significación estadística.
Decidí buscar en Google la palabra "valor p" y lo que encontré en Wikipedia me confundió aún más ...
Al probar hipótesis estadísticas, el valor p o valor de probabilidad para un modelo estadístico dado es la probabilidad de que, si la hipótesis nula es verdadera, el resumen estadístico (por ejemplo, el valor absoluto de la media muestral de la diferencia entre dos grupos comparados) sea mayor o igual que los resultados observados reales.Buen trabajo, Wikipedia.
- Wikipedia
Bueno. No entendí qué significa realmente el valor p.
A medida que profundizaba en el campo de la ciencia de datos, finalmente comencé a comprender el significado del valor p y dónde se puede usar como parte de las herramientas de toma de decisiones en ciertos experimentos.
Así que decidí explicar el valor p en este artículo, así como cómo se puede utilizar en la prueba de hipótesis, para brindarle una comprensión mejor y más intuitiva de los valores p.
Además, no podemos perder una comprensión fundamental de otros conceptos y la definición de p-valor, prometo que haré esta explicación intuitiva sin exponerlos a todos los términos técnicos que encontré.
Hay cuatro secciones en total en este artículo para brindarle una imagen completa desde la construcción de una prueba de hipótesis hasta la comprensión del valor p y su uso en su proceso de toma de decisiones. Le recomiendo encarecidamente que los revise todos para obtener una comprensión detallada de los valores p:
- Prueba de hipótesis
- Distribución normal
- ¿Qué es un valor P?
- Significancia estadística
Será divertido.
¡Empecemos!
1. Prueba de hipótesis
Antes de hablar sobre lo que significa el valor p, comencemos por mirar las pruebas de hipótesis , donde el valor p se usa para determinar la significancia estadística de nuestros resultados.
Nuestro objetivo final es determinar la importancia estadística de nuestros resultados.
Y la importancia estadística se basa en estas 3 ideas simples:
- Prueba de hipótesis
- Distribución normal
- Valor p
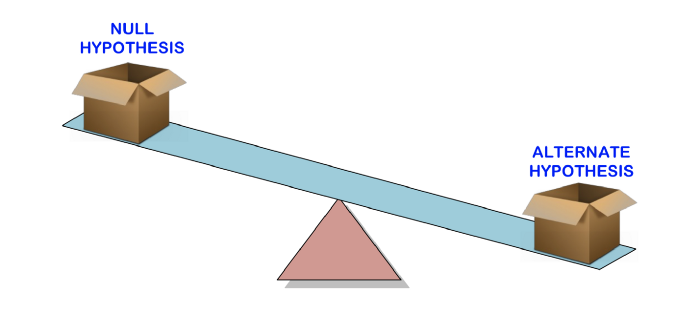
La prueba de hipótesis se usa para probar la validez de una declaración (hipótesis nula) hecha sobre una población usando datos de muestra. Una hipótesis alternativa es aquella en la que creerías si la hipótesis nula resultara ser incorrecta.
En otras palabras, crearemos un reclamo (hipótesis nula) y usaremos los datos de muestra para verificar si el reclamo es válido. Si el enunciado no es verdadero, elegiremos una hipótesis alternativa. Todo es muy sencillo.
Para saber si una afirmación es válida o no, usaremos el valor p para sopesar la fuerza de la evidencia y ver si es estadísticamente significativa. Si la evidencia apoya la hipótesis alternativa, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Esto se explicará en la siguiente sección.
Usemos un ejemplo para aclarar este concepto, y este ejemplo se usará a lo largo de este artículo para otros conceptos.
Ejemplo. Suponga que el tiempo de entrega de reclamaciones de una pizzería es de 30 minutos o menos en promedio, pero usted cree que es más largo de lo que afirma. Entonces haces una prueba de hipótesis y seleccionas al azar un tiempo de entrega para probar la afirmación:
- — 30
- — 30
- , , — — , .
Utilizaremos una prueba unidireccional en nuestro caso, ya que solo es importante para nosotros que el tiempo medio de entrega supere los 30 minutos. No consideraremos esta posibilidad en el sentido contrario, ya que las consecuencias de que el tiempo medio de entrega sea menor o igual a 30 minutos son aún más preferibles. Aquí queremos comprobar si existe la posibilidad de que el tiempo medio de entrega sea superior a 30 minutos. En otras palabras, queremos ver si la pizzería nos ha engañado.
Una de las formas comunes de probar hipótesis es mediante la prueba Z. No entraremos en detalles aquí, ya que queremos comprender mejor lo que sucede en la superficie antes de sumergirnos más profundamente.
2. Distribución normal
La distribución normal es una función de densidad de probabilidad que se utiliza para ver la distribución de datos.
La distribución normal tiene dos parámetros, la media (μ) y la desviación estándar, también llamada sigma (σ).
La media es la tendencia central en la distribución. Define la ubicación del pico para distribuciones normales. La desviación estándar es una medida de variabilidad. Determina qué tan lejos de la media tienden a caer los valores.
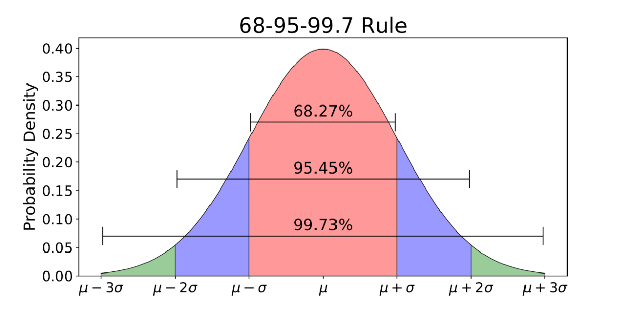
La distribución normal generalmente se asocia con la regla 68-95-99.7 (imagen de arriba).
- 68% de los datos están dentro de 1 desviación estándar (σ) de la media (μ)
- 95% de los datos están dentro de 2 desviaciones estándar (σ) de la media (μ)
- 99,7% de los datos están dentro de 3 desviaciones estándar (σ) de la media (μ)
¿Recuerda el umbral de cinco sigma para el bosón de Higgs del que hablé al principio? 5 sigma es aproximadamente el 99,99999426696856% de los datos que deben recibirse antes de que los científicos confirmen el descubrimiento del bosón de Higgs. Este fue un umbral estricto establecido para evitar posibles señales falsas.
Frio. Ahora puede que se esté preguntando: "¿Cómo se relaciona la distribución normal con nuestra prueba de hipótesis anterior?"
Dado que usamos la prueba Z para probar nuestra hipótesis, necesitamos calcular las puntuaciones Z (que se utilizarán en nuestras estadísticas de prueba), que son el número de desviaciones estándar de la media del punto de datos. En nuestro caso, cada dato es el tiempo de entrega de la pizza que recibimos. Tenga en cuenta que cuando calculamos todos los puntajes Z para cada tiempo de entrega de pizza y trazamos una curva de distribución normal estándar como se muestra a continuación, la unidad en el eje X cambiará de minutos a la unidad de desviación estándar, ya que estandarizamos la variable restando la media y dividiendo es por la desviación estándar (consulte la fórmula anterior). Examinar la curva de campana estándar es útil porque podemos comparar los resultados de la prueba con una población "normal" con una unidad estandarizada en desviación estándar, especialmente cuando tenemos una variable que viene con diferentes unidades.

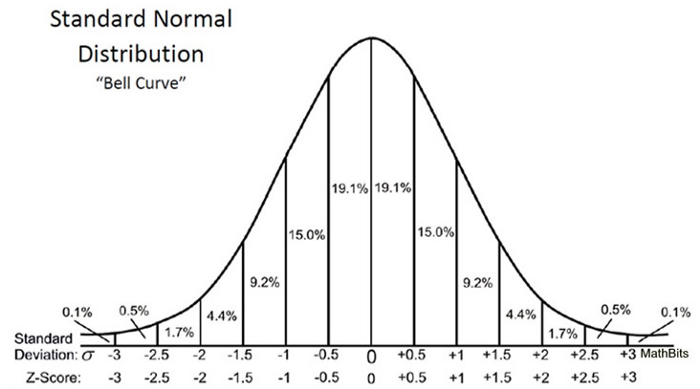
Un puntaje z puede decirnos dónde se encuentran los datos generales en comparación con la población promedio.
Me gusta la forma en que Will Cursen lo expresó: cuanto mayor o menor sea la puntuación Z, menos probable será un resultado aleatorio y más probable será un resultado significativo.
Pero, ¿qué tan alto (o bajo) se considera lo suficientemente convincente para cuantificar la importancia de nuestros resultados?
Clímax
Aquí, necesitamos la última pieza para resolver el rompecabezas, el valor p, y verificar si nuestros resultados son estadísticamente significativos según el nivel de significancia (también conocido como alfa) que establecimos antes de comenzar nuestro experimento.
3. ¿Qué es el valor P?
Finalmente ... ¡Estamos hablando de valor p aquí!
Todas las explicaciones anteriores están destinadas a sentar las bases y llevarnos a este valor P. Necesitamos un contexto y pasos previos para comprender este valor p misterioso (en realidad no tan misterioso) y cómo puede llevarnos a tomar decisiones para probar la hipótesis.
Si has llegado hasta aquí, sigue leyendo. ¡Porque esta sección es la parte más emocionante de todas!
En lugar de explicar los valores p usando la definición dada por Wikipedia (lo siento Wikipedia), vamos a explicarlo en nuestro contexto: ¡tiempo de entrega de pizza!
Como recordatorio, hemos seleccionado aleatoriamente algunos tiempos de entrega de pizzas, y el objetivo es verificar si el tiempo de entrega supera los 30 minutos. Si la evidencia final respalda la afirmación de la pizzería (el tiempo de entrega promedio es de 30 minutos o menos), entonces no rechazaremos la hipótesis nula. De lo contrario, refutamos la hipótesis nula.
Entonces, el trabajo del valor p es responder esta pregunta:
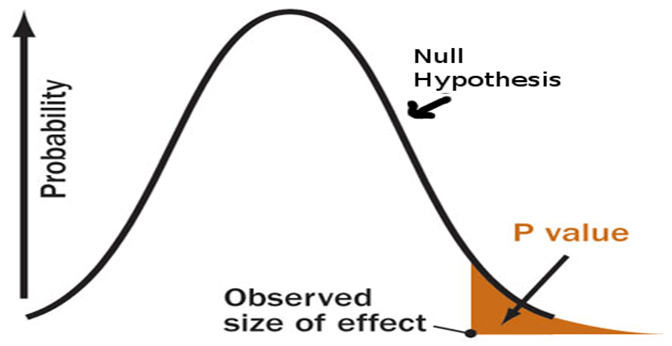
Si vivo en un mundo donde los tiempos de entrega de pizzas son 30 minutos o menos (la hipótesis nula es correcta), ¿qué tan inesperada es mi evidencia en la vida real?El valor p responde a esta pregunta con un número: una probabilidad.
Cuanto menor sea el valor p, más inesperada será la evidencia y más ridícula se verá nuestra hipótesis nula.
¿Y qué hacemos cuando nos sentimos ridículos por nuestra hipótesis nula? Lo rechazamos y elegimos nuestra hipótesis alternativa.
Si el valor p está por debajo de un nivel de significancia dado (la gente lo llama alfa, yo llamo a esto el umbral del absurdo; no preguntes por qué, es más fácil de entender para mí), entonces rechazamos la hipótesis nula.
Ahora entendemos lo que significa el valor p. Apliquemos esto en nuestro caso.
Valor p en el cálculo del tiempo de entrega de la pizza
Ahora que hemos recopilado algunos datos de muestra sobre los tiempos de entrega, realizamos el cálculo y encontramos que el tiempo medio de entrega es 10 minutos más largo con un valor p de 0,03.
Esto significa que en un mundo donde los tiempos de entrega de pizzas son 30 minutos o menos (la hipótesis nula es correcta), existe un 3% de probabilidad de que veamos el tiempo de entrega promedio al menos 10 minutos más debido al ruido aleatorio. ...
Cuanto menor sea el valor p, más significativo será el resultado, porque es menos probable que sea causado por ruido.
En nuestro caso, la mayoría de la gente malinterpreta el valor p:
Un valor p de 0.03 significa que hay un 3% (porcentaje de probabilidad) de que el resultado se deba al azar, lo cual no es cierto.La gente a menudo quiere una respuesta definitiva (incluido yo mismo), razón por la cual me he confundido durante mucho tiempo con la interpretación de los valores p.
El valor p no * prueba * nada. Es solo una forma de utilizar la sorpresa como base para una decisión inteligente.Así es como podemos usar un valor p de 0.03 para ayudarnos a tomar decisiones inteligentes (IMPORTANTE):
- Cassie Kozyrkov
- Imagínese que vivimos en un mundo donde el tiempo medio de entrega es siempre de 30 minutos o menos, ¡porque creemos en la pizzería (nuestra creencia original)!
- Después de analizar el tiempo de entrega de las muestras recolectadas, el valor p es 0.03 menor que el nivel de significancia de 0.05 (suponiendo que establezcamos este valor antes de nuestro experimento), y podemos decir que el resultado es estadísticamente significativo.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
A estas alturas, es posible que haya descubierto algo ... Dependiendo de nuestro contexto, los valores p no se utilizan para probar o justificar nada.
En mi opinión, los valores p se utilizan como una herramienta para desafiar nuestra creencia inicial (hipótesis nula) cuando el resultado es estadísticamente significativo. En el momento en que nos sentimos ridículos con nuestra propia creencia (asumiendo que el valor p indica que el resultado es estadísticamente significativo), descartamos nuestra creencia original (rechazamos la hipótesis nula) y tomamos una decisión inteligente.
4. Importancia estadística
Finalmente, esta es la última etapa en la que juntamos todo y comprobamos si el resultado es estadísticamente significativo.
No es suficiente tener solo un valor p, necesitamos establecer un umbral (nivel de significancia - alfa). Alpha siempre debe establecerse antes de experimentar para evitar sesgos. Si el valor p observado es menor que alfa, concluimos que el resultado es estadísticamente significativo.
La regla básica es establecer alfa en 0.05 o 0.01 (nuevamente, el valor depende de su tarea).
Como se mencionó anteriormente, suponga que establecemos el alfa en 0.05 antes de comenzar el experimento, el resultado es estadísticamente significativo ya que el valor p de 0.03 es menor que el alfa.
Como referencia, a continuación se muestran los pasos principales para todo el experimento:
- Formular la hipótesis nula
- Formule una hipótesis alternativa
- Determine el valor alfa a utilizar
- Encuentre el puntaje Z asociado con su nivel alfa
- Encuentre estadísticas de prueba usando esta fórmula
- Si la estadística de la prueba es menor que la puntuación Z alfa (o el valor p es menor que el valor alfa), rechace la hipótesis nula. De lo contrario, no rechace la hipótesis nula.
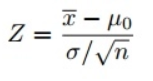
Si desea saber más sobre la significación estadística, no dude en consultar este artículo: Explicación de la significación estadística , escrito por Will Kersen .
Reflexiones posteriores
Hay mucho que digerir aquí, ¿no?
No puedo negar que los valores p son intrínsecamente confusos para muchas personas, y me tomó bastante tiempo comprender y apreciar realmente los valores p y cómo podrían aplicarse dentro de nuestro proceso de toma de decisiones. como científicos de datos.
Pero no confíe demasiado en los valores p, ya que solo ayudan en una pequeña parte de todo el proceso de toma de decisiones.
Espero que mi explicación de los valores p se haya vuelto intuitiva y útil para comprender qué significan realmente los valores p y cómo se pueden utilizar para probar sus hipótesis.
Calcular los valores p es simple en sí mismo. La parte difícil llega cuando queremos interpretar los valores p en las pruebas de hipótesis. Con suerte, ahora la parte difícil se vuelve un poco más fácil para ti.
Si desea obtener más información sobre estadística, le recomiendo que lea este libro (¡que estoy leyendo actualmente!): Estadísticas prácticas para científicos de datos, especialmente escrito para que los científicos de datos comprendan los conceptos fundamentales de la estadística.

Descubra los detalles de cómo obtener una profesión de alto perfil desde cero o subir de nivel en habilidades y salario tomando los cursos en línea pagados de SkillFactory:
- Formación para la profesión de Data Science desde cero (12 meses)
- Profesión analista con cualquier nivel inicial (9 meses)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- 450
- Data Science : «data»
- Data Sciene : Decision Intelligence