Aproximación lineal de una combinación de líneas por un conjunto de puntos ruidosos

Formulación del problema

Consideremos el problema de la aproximación de una combinación de líneas rectas por un conjunto de coordenadas ruidosas de puntos ubicados en una combinación dada de líneas (ver Fig. 1 y Fig. 2). La fórmula habitual de aproximación lineal no funcionará aquí, ya que los puntos están mezclados y el resultado será una línea promediada entre ellos (ver Fig. 3).

Figura: 1 combinación de líneas y un conjunto de coordenadas ruidoso

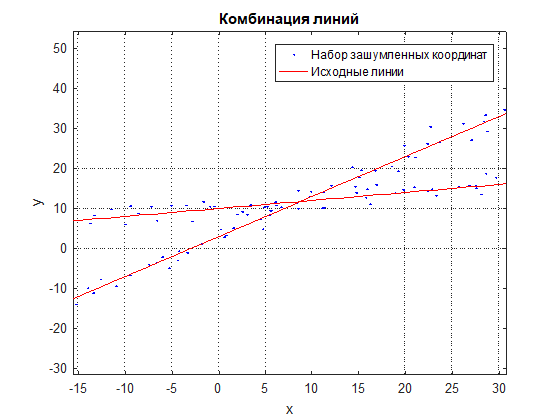
Figura: 2 Una combinación de líneas y un conjunto ruidoso de coordenadas en una escala ampliada

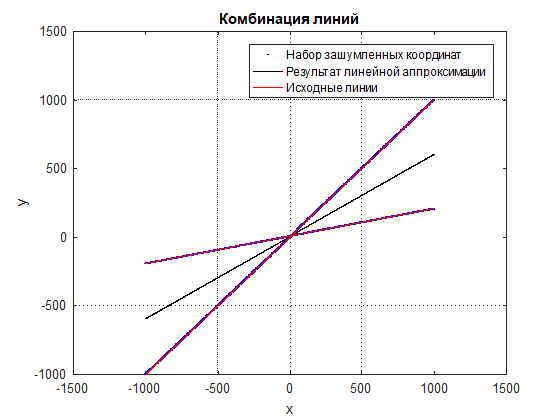
Figura: 3 Resultado de aproximación lineal

Algoritmo

, , . .. , , -90 +90 ( -180 180 , .. ).

, , . , , . .

, , . , , .

1.

. , . , . -90 90 0.1 .

2.

, .

, , :

$$

$$y = kx + b, x_p, y_p$$

, , , :

$$

$$y-y_p=-(x-x_p)/k =>y= -x/k+ x_p/k+y_p$$

, :

$$

$$-x/k+ x_p/k+y_p=kx+b => -x+ x_p+ky_p= k^2 x+bk$$

$$

$$-bk+ x_p+ky_p= k^2 x+x => x= (x_p+ky_p-bk)/(k^2+1)$$

$$

$$y= k (x_p+ky_p-bk)/(k^2+1)+b= (〖kx〗_p+k^2 y_p-bk^2+bk^2+b)/(k^2+1)=(〖kx〗_p+k^2 y_p+b)/(k^2+1)$$

:

$$

$$dist= √((x_p- (x_p+ky_p-bk)/(k^2+1))^2+(y_p- (〖kx〗_p+k^2 y_p+b)/(k^2+1))^2 )$$

3.

, , , (. . 4-6).

. , (. . 7, 8). . 7 , .

. 4 ( )

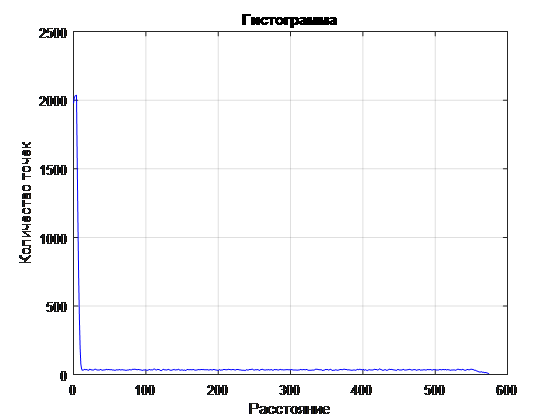
. 5 ( )

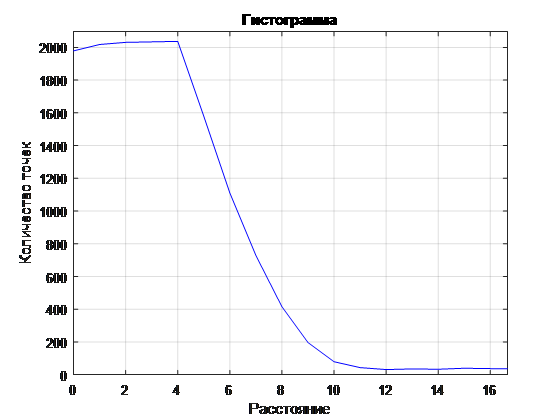
. 6 ( )

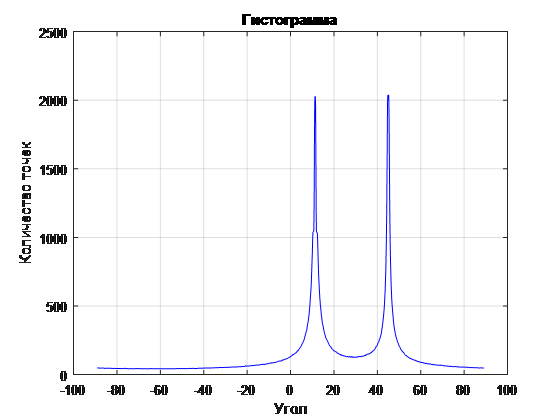
. 7 ( 1)

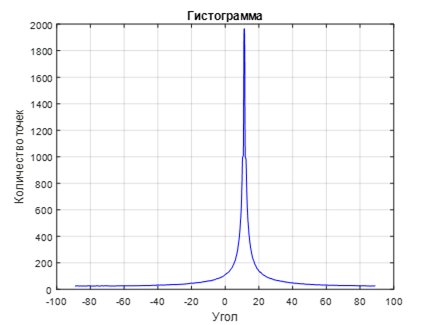
. 8 ( 2)

4.

, . , (. . 9 . 10):

$$

$$k= (N∑_1^N(xy)- ∑_1^Nx ∑_1^Ny)/(N∑_1^Nx^2 - (∑_1^Nx)^2 ); b =(∑_1^Ny-k∑_1^Nx)/N$$

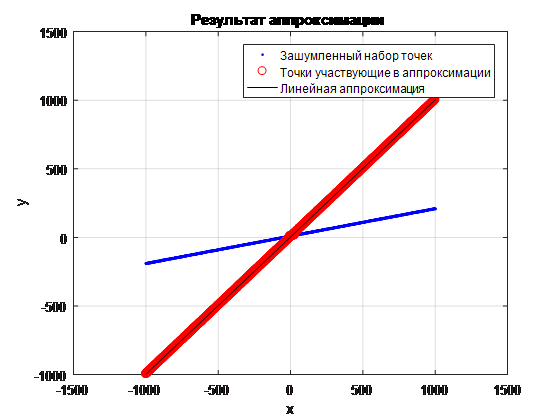
. 9

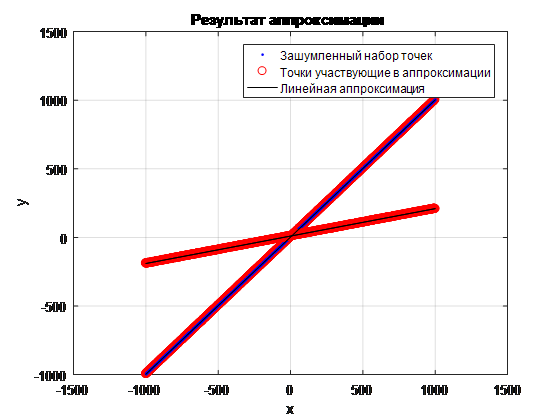
. 10

(. 11-13).

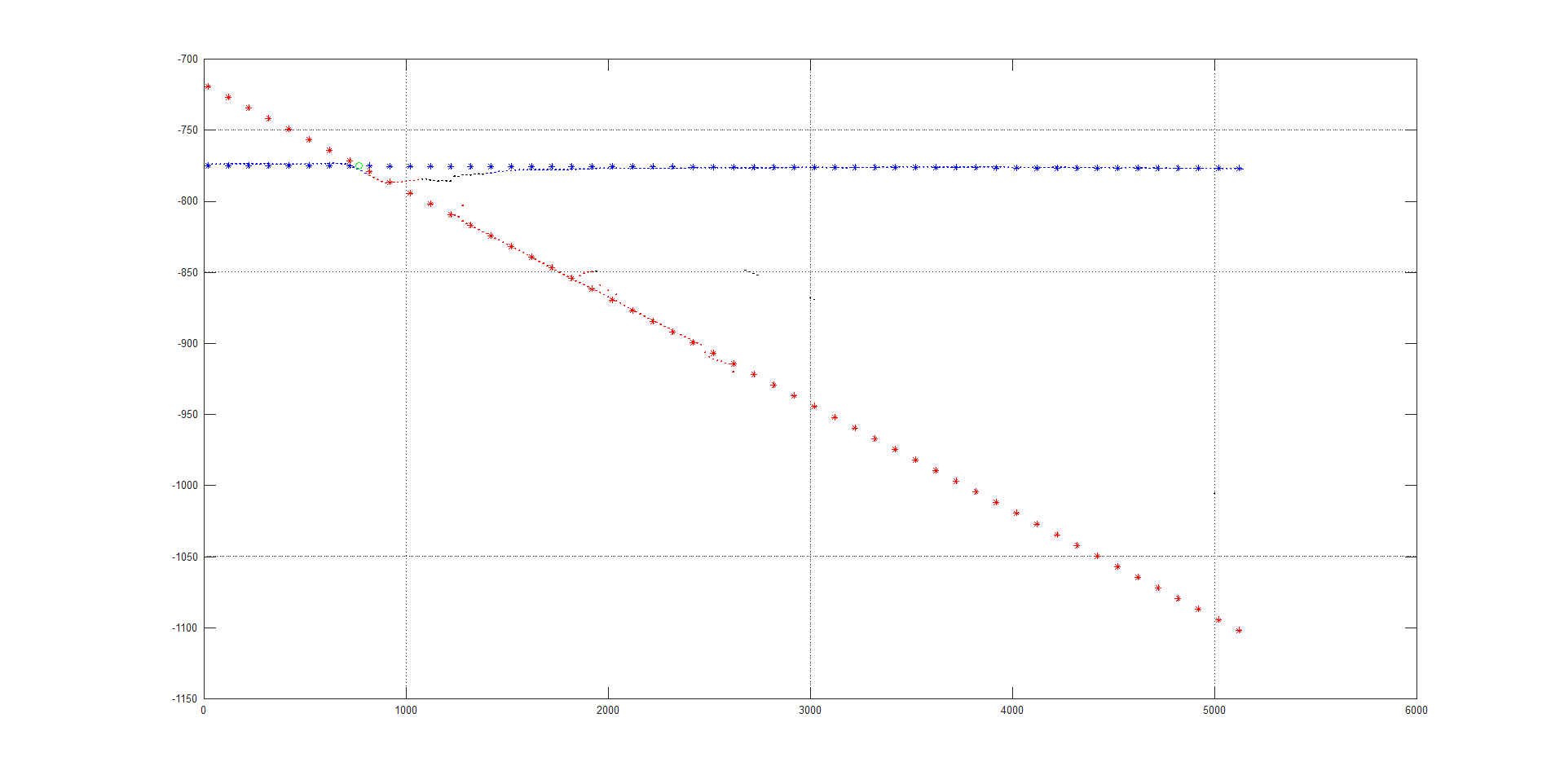
. 11

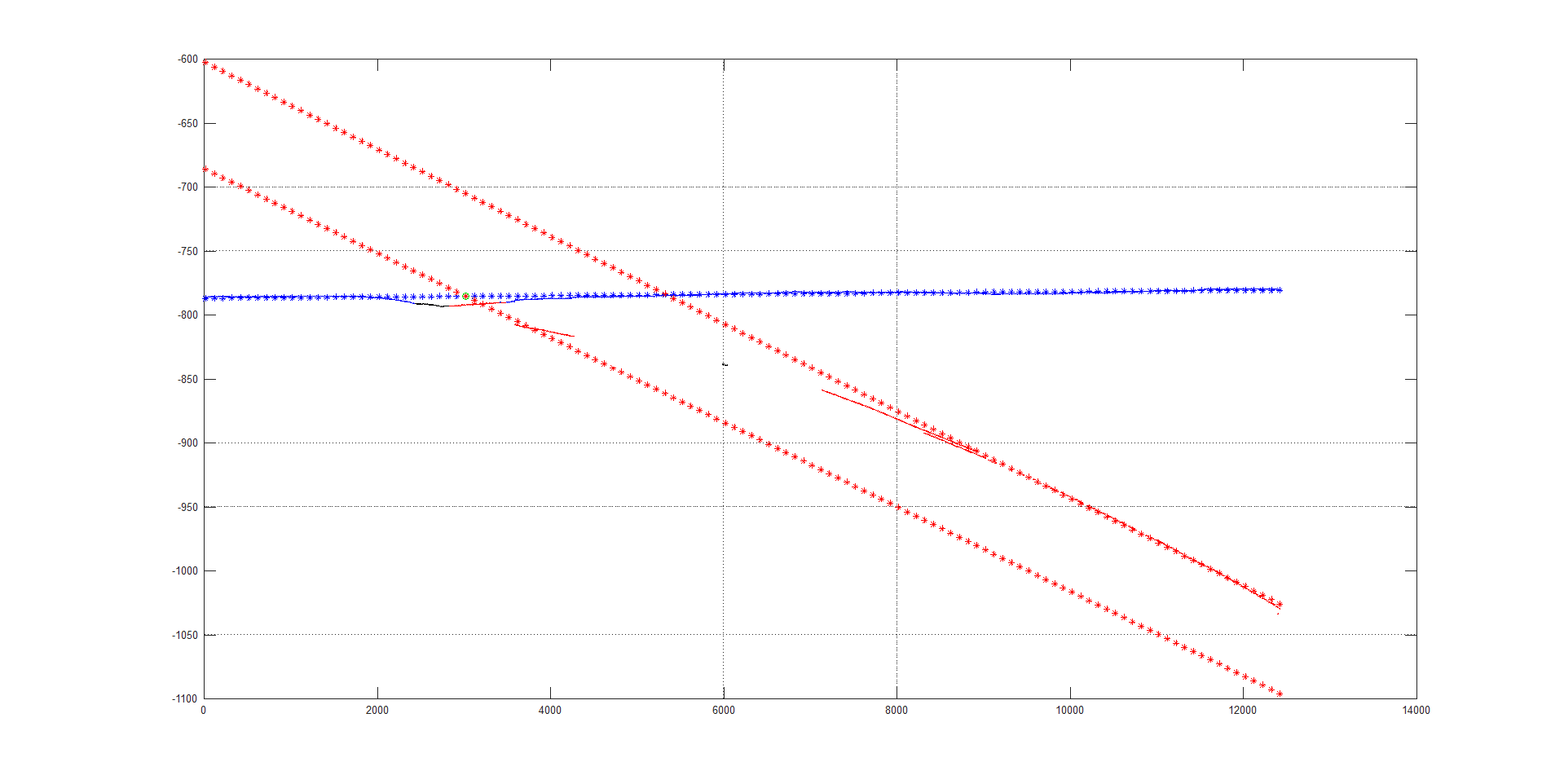
. 12

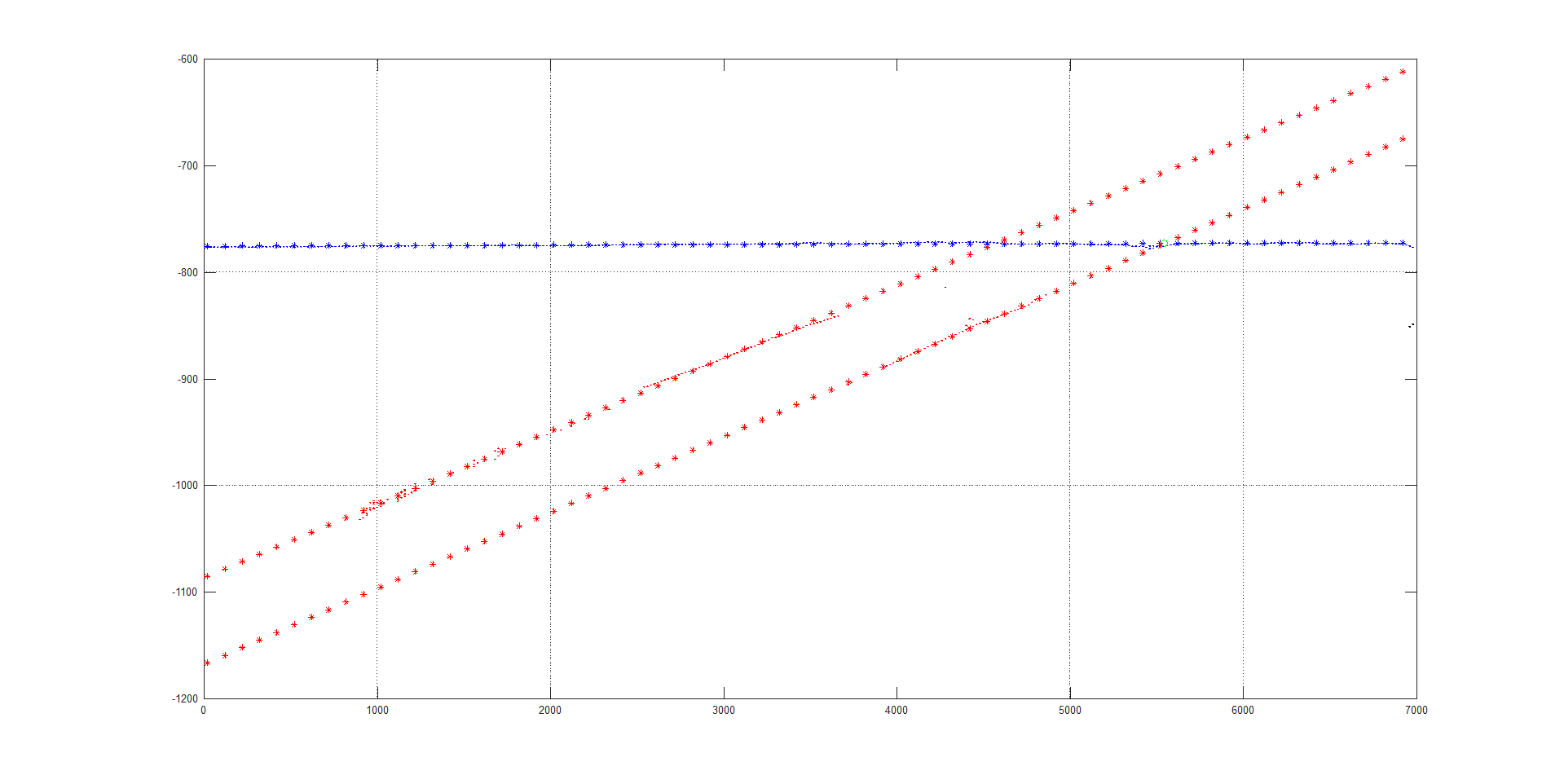
. 13

( ). .

, , , , .

El objetivo principal de este artículo es ver desde afuera si alguien ha encontrado problemas similares y cómo los resolvió. De repente, hay formas de detectar estas líneas en una sola pasada. Vea algunas soluciones interesantes que se pueden utilizar en otras tareas.