Otros artículos del ciclo
Después de una presentación detallada con detalles de transformaciones individuales, con elementos de un campo algebraico finito, no abstracto (como en muchas publicaciones, sin excluir el Khabrovsky), sino ( concreto ), dentro del cual se implementan RIJNDAEL, AES-128 y ( realizando operaciones del estándar AES-128 ) , podemos pasar a considerar posibles ataques al cifrado. Por ahora, nos limitaremos a un ataque, en nuestra opinión, el más comprensible y transparente construido (aunque, quizás, no para todos los lectores) Habr.
Ya estoy acostumbrado a las desventajas, pero con lo que diablos no bromea. El análisis de posibles ataques y resultados esperados ha sido realizado por muchos autores, pero evidentemente no basta con ejemplos concretos de éxito o diseños simplemente impresionantes. Aquí consideraremos desde un punto de vista matemático un ataque utilizando un error introducido por el intruso en el texto cifrado. Al elegir un ataque para una demostración, el autor trató de no involucrar a aquellos donde se utilizan cosas matemáticas demasiado retorcidas y abstrusas, pero el tema en cuestión es bastante serio y no permite pasar a explicaciones sobre los "dedos".
Un objetivo importante de la publicación es mostrar la aplicación de las matemáticas, que forma la base de AES-128, y que, lamentablemente, muchos autores eluden o interpretan falsamente infundadas y sin fundamento, guiados por el hecho de que pocos pueden verificar y señalar sus invenciones.
El material del artículo no es completamente el concepto original del ataque, las principales acciones se toman del trabajo , pero fue cuidadosamente elaborado, complementado y probado experimentalmente por mis alumnos. Obtuvieron buenas prácticas tanto en álgebra superior como en criptología.
1. Ataque a la clave de cifrado AES
Primero, un ataque a AES se describe en un caso simple, y luego queda claro cómo se puede generalizar dicho ataque. El objetivo del ataque en cuestión es recuperar la clave K (Nr) del cifrado. Una vez que se determina la clave parcial (redonda) K (Nr), resulta fácil obtener la clave K.
1.1 Principio de ataque
Se supone que es posible cambiar introduciendo el error "ε" en un byte separado de la matriz S del estado (uno de 16) después de la operación ShiftRows (Nr - 1), es decir, la penúltima ronda, y el índice (# de la celda) del byte corrupto (elemento ) estado. Esta última hipótesis se puede omitir, fue introducida para explicar más fácilmente el mecanismo de ataque. Se supone que el nuevo valor del elemento de estado es desconocido.
El error "ε" se extiende a no más de cuatro bytes del estado de salida del proceso. Para los 4 elementos modificables del estado de salida, se encuentra un conjunto de valores (conjunto) de vectores de posible error "ε" en la sección 1.4. Además, es posible intersecar los conjuntos de valores posibles "ε" (definición 1) para estos cuatro elementos. Cuando estos conjuntos se cruzan, se obtiene un conjunto más pequeño y, por tanto, se reduce el número de textos cifrados necesarios para un análisis completo.
Finalmente, para cada error, imprimimos algunos posibles valores confusos para los cuatro elementos de la clave de ronda anterior. Formando otros textos cifrados, encontramos cuatro bytes de la clave redonda K (10). Este ataque sigue siendo exitoso incluso con muchas suposiciones generales sobre la ubicación del error. Como la falta de información sobre la ubicación del error antes de la novena transformación MixColumns (). La diferencia entre la matriz de texto cifrado con y sin distorsiones revelará las distorsiones y su posición (en el ejemplo, estas son posiciones 0,7,10,13).
También se sugiere que los errores "ε" introducidos en la ronda 8 (antes de la 8ª transformación MixColumns ()) podrían ser útiles para el análisis. Pero al mismo tiempo, aumenta el número de textos cifrados necesarios para un análisis más completo. Para el ejemplo numérico en consideración, se necesitan alrededor de diez textos cifrados para obtener cuatro bytes de la clave redonda K (10), en condiciones en las que no se considera la hipótesis de ubicaciones de error.
1.2 Ejemplo numérico del impacto de un error en un mensaje
Aquí se usa el mismo ejemplo que se da en el Apéndice del trabajo mencionado . Se consideran las penúltimas y últimas rondas del proceso de cifrado (la representación en bytes de los datos tiene la forma):
Entrada = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';
Clave de cifrado = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';
Salida = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';
Error "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00'.
El siguiente diagrama muestra los valores contenidos en las matrices de estado según la longitud del bloque de cifrado y la longitud de la clave de cifrado de 16 bytes cada uno (es decir, Nb = 4 y Nk = 4).
La propagación del error se muestra en negrita y notación hexadecimal. A continuación se muestran las casillas del Estado en diferentes situaciones:
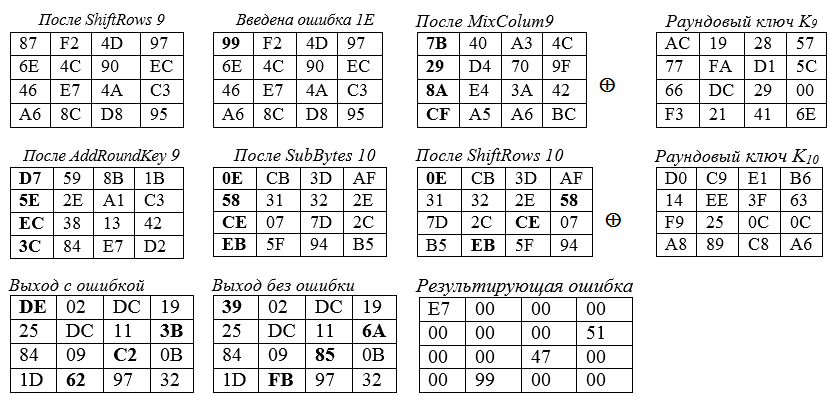
El error "ε" = 1E, insertado en el byte 0 del estado de la novena ronda, produce cambios en los cuatro bytes del estado final. Ejemplos de cálculos para las celdas de las esquinas de la diagonal principal del "cuadrado" del estado:
- el error "ε" = 1E
87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
se ingresa en la celda superior izquierda (esquina) del cuadrado de estado de la novena ronda - parte inferior derecha el ángulo de estado de la novena ronda después de MixColum9 se suma con el byte clave K (9):
BC ⊕ 6E = 1011 1100 11 0110 1110 = 1101 0010 = d2.
- cálculo de los valores del error resultante.
En presencia de dos textos de mensaje, con y sin error, los valores y posiciones de los bytes de estado corruptos se determinan restando un texto del otro. En nuestro caso, dicha resta se puede reemplazar sumando los textos módulo dos. Obtenemos un resultado distinto de cero solo para los bytes cambiados por un error introducido en el texto fuente.
Por ejemplo, en forma hexadecimal, encontramos los valores de error:
Tabla 7 - cálculo de valores de error
Como resultado, los errores de diferencia... Pongamos un ejemplo de
cómo calcular el último byte de error: 62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.
Posiciones de los bytes de estado cambiadas por el error
Indique los índices para los elementos de la clave de ronda (última ronda), como K [0], K [7], K [10], K [13]. Aquí, 0, 7, 10, 13 son los números de celda de la matriz de estado, y la matriz Ao es la matriz de transformación para mezclar las columnas del proceso de cifrado, cuya primera columna es: '02', '01', '01', '03'.
Cómo un error inyectado afecta el estado final final
Análisis de la información obtenida cuando se introduce un error
La única operación que puede contener información sobre la clave K (Nr) es la última transformación SubBytes (). Por lo tanto, tenemos cuatro ecuaciones, donde x0, x1, x2, x3, ε son variables desconocidas.
Queremos obtener soluciones para las siguientes cuatro ecuaciones:
Bytes modificado por un error contienen información sobre la clave desconocida que generó estos bytes.
Todas estas ecuaciones se pueden generalizar en una sola ecuación
s (x + cε) + s (x) = ε ', (1)
donde el valor constante =' 01 ',' 02 'o' 03 'y es esta ecuación la que resolveremos y analizar.
Definición 1 . El conjunto de soluciones de la ecuación (1) para errores ε se denota con el símbolo B (cε ') y se define mediante la expresión:
B (cε') = S (cε ') = {ε є GF [2 8 ]: ∃ x є GF [2 8 ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.
Ésta es un área de error individual correspondiente a un error específico ε '. Para otros ε ', las áreas de error serán diferentes.
Definición 2 . Considere una transformación lineal ℓ sobre el campo GF (2):
ℓ: GF [2 8 ] → GF [2 8 ];
x → x 2 + x.
La imagen de ℓ es un mapeo del espacio vectorial Im (ℓ) GF (2), es decir, el conjunto de elementos
(x 2 + x) de GF [2 8 ] denotamos 1 = Im (ℓ) y su dimensión dimGF (2) (E1) = 7. Si θ є 1, entonces hay dos soluciones diferentes x1, x2 є GF [ 2 8 ] ecuaciones x 2 + x = θ, y las soluciones satisfacen la relación x2 = x1 + 1 y x2 ∙ x1 = θ (modd φx, (2 8 -1)) según el teorema de Vieta.
La variable θ es un término libre de una ecuación cuadrática
Ilustremos la transformación lineal considerada con un ejemplo.
Ejemplo El campo GF está configurado [2 8], la transformación x → x 2 + x se realiza sobre sus elementos .
Tabla 8 - el fragmento inicial del campo GF [2 8 ] y los resultados de la transformación de elementos.
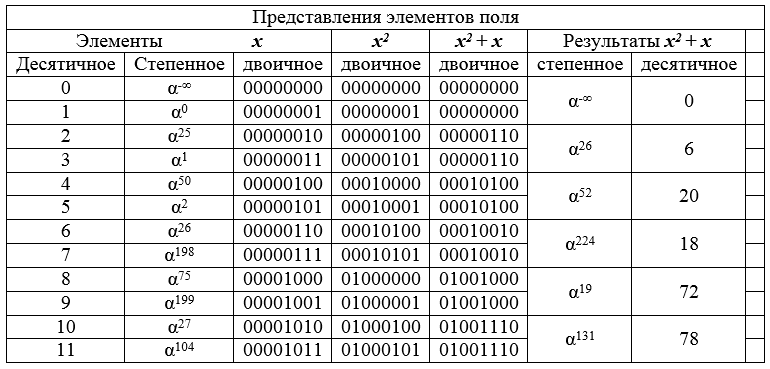
La Tabla 8 muestra cómo la conversión cambia los pares adyacentes en una lista ordenada por decimales al mismo elemento de campo. De esto se deduce que el resultado de la transformación (imagen) es la mitad de la preimagen (el campo está, por así decirlo, comprimido por un factor de 2). Este principio de contracción de la dimensión de conjuntos constituye la base del ataque propuesto.
Proposición 2 . La siguiente afirmación es cierta para λ1, λ2 є GF [2 8 ] - {0}:
2. Generalización e implementación
En primer lugar, utilizando una aplicación de software especial, se generan 20 textos cifrados con un error. Para ello, el texto fuente, la clave, el error se ingresan en el modelo (programa) y se establece el número de posición en el que se coloca el error. Al presionar el botón "Inicio", el programa implementa el algoritmo y muestra los resultados de las últimas 2 rondas de cifrado en forma expandida para texto con error, texto sin error y la diferencia entre ellos. Después de eso, el texto cifrado se guarda sin error y con error. El valor de error se cambia cíclicamente y al presionar el botón "Inicio" se obtiene el siguiente texto cifrado con un error. Se formaron 5 textos cifrados con un error en un valor de la columna.
Para implementar el ataque, debe abrir un archivo con texto cifrado sin error y texto cifrado con error utilizando el programa (los datos del archivo se presentan en forma hexadecimal), los textos cifrados y la diferencia entre ellos se muestran como una matriz cuadrada de bytes (Estado). Pulsando el botón “Buscar clave” se inicia el procedimiento de búsqueda de posibles bytes de la clave. El estado actual de los procesos se muestra en un cuadro de texto. Después de eso, se abre un texto cifrado con otro error y se repite el procedimiento. Cuando se recibe un byte de clave redonda de 10, también aparece en la matriz de bytes cuadrados correspondiente. Cuando se ejecutan los 20 textos cifrados generados en la etapa anterior con un error, existe una alta probabilidad de obtener los valores de todos los bytes de la clave de la ronda 10 (de lo contrario, se necesitan más textos cifrados con errores).Después de eso, restaure la clave de cifrado de acuerdo con el algoritmo "Recuperación de clave de cifrado usando la última subclave" proporcionadoaquí .
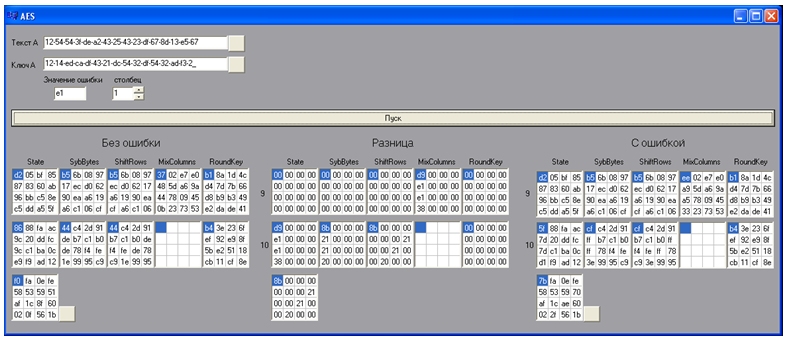
Figura 11 - Producto de software para construir un texto cifrado con un error
Para acelerar el procedimiento de enumeración de textos cifrados con un error, puede poner una marca delante del botón "Buscar clave"
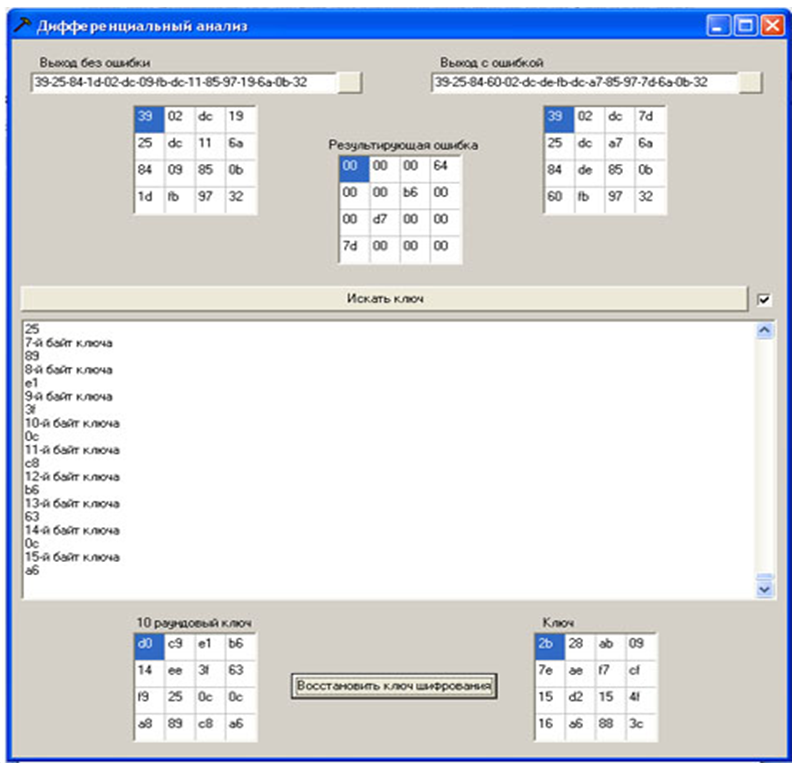
Figura 12 - Implementación de software de un ataque
Ejemplo de un producto de software:
Código fuente 3243f6a8885a308d313198a2e0370734
Clave 2b7e151628aed2a6abf7158809cf4f3c
Error 1 1e00000000000000000000000000000000000000
Texto cifrado con error 1
Posibles bytes de25c0941d02bd
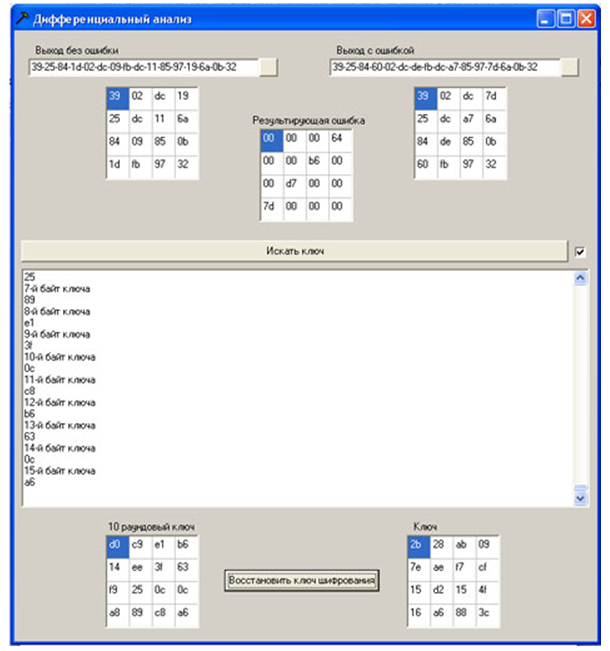
Figura 13 - Un ejemplo de la operación del programa. La
clave de Ronda 10 d014f9a8c9ee2589e13f0cc8b6630ca6 está completamente recuperada.
Clave recuperada 2b7e151628aed2a6abf7158809cf4f3c, como se esperaba, coincide con la clave especificada en la sesión de cifrado.
2.1. Situación en la que no hay información sobre la ubicación del error
En este punto, se supone que el error está contenido en el byte de estado entre las dos últimas ejecuciones de la operación MixColumns. Este es el mismo caso, excepto por el hecho de que el error se puede encerrar entre bytes de 1 a 16. El error se multiplica por la operación MixColumns y se extiende a 4 bytes de estado.
El error forzado se genera en la primera fila de la matriz de estado diferencial. Aquí es posible determinar a qué columna pertenece el error ingresado mirando la columna de error forzado. Esto se hace examinando las cuatro posibles posiciones de línea para el error ingresado usando el método descrito en la descripción anterior.
2.2. Dispositivo de hardware
Supongamos que tiene la capacidad de interferir físicamente con un dispositivo de hardware AES. Primero, calculemos cifrados para más de diez textos sin formato aleatorios usando un dispositivo AES. Luego cambiamos el proyecto de ejemplo cortando las líneas y conectándolas al suelo (o Vcc) temporalmente entre dos bytes durante la ronda, localizados dos rondas antes de completar. Después de todo, tenemos un byte en la ronda Nk -2, siempre reemplazado por '00' (o 'FF').
Calculamos otra vez el mismo mensaje con el dispositivo de actuación. Con texto plano aleatorio, un byte defectuoso es como un error aleatorio. Este único error se traduce en cuatro errores en la ronda Nk -1 y dieciséis errores en la ronda Nk. En este caso, se puede obtener una matriz de desviación (diferencial), con la ayuda de la cual es posible, analizando el error, encontrar la última clave de ronda.
Literatura:
[1] FIPS PUB 197: Estándar de cifrado avanzado, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo y Lipton, Sobre la importancia de verificar los protocolos criptográficos en busca de fallas, Lecture Notes in Computer Science, Advances in Cryptology, actas de EU-ROCRYPT'97, pp. 37-51, 1997.
[3] E. Biham y A. Shamir, Análisis diferencial de fallas de criptosistemas de clave secreta, CS 0910, Actas de Crypto'97.
[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance - a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, California, 18-21 de noviembre de 1996, págs. 1-11, ISBN 1-880446- 83-9.