Redes Bayesianas con Python - Explicado con ejemplos
Debido a la información limitada (especialmente en ruso nativo) y los recursos de trabajo, las redes bayesianas están rodeadas de una serie de problemas. Y uno podría dormir bien si no se implementaran en la mayoría de las tecnologías avanzadas de la época, como la inteligencia artificial y el aprendizaje automático.
Basado en este hecho, este artículo está completamente dedicado al trabajo de las redes bayesianas y cómo ellos mismos no pueden formar problemas, sino que se aplican en su solución, incluso si los problemas que se resuelven son extremadamente confusos.
Estructura del artículo
- ¿Qué es una red bayesiana?
- ¿Qué son los gráficos acíclicos dirigidos?
- Qué matemática hay en las redes bayesianas
- Un ejemplo que refleja la idea de una red bayesiana
- La esencia de la red bayesiana
- Red bayesiana en Python
- Aplicación de redes bayesianas
Vamonos.
¿Qué es una red bayesiana?
Las redes bayesianas entran en la categoría de modelos gráficos probabilísticos (GPM). Los VGM se utilizan para calcular la variabilidad para la aplicación en conceptos de probabilidad.
El nombre común para las redes bayesianas es Redes profundas. Se utilizan para modelar gráficos acíclicos dirigidos.
¿Qué son los gráficos acíclicos dirigidos?
Un gráfico acíclico dirigido (como cualquier gráfico en estadísticas) es una estructura de nodos y enlaces, donde los nodos son responsables de algunos valores, y los enlaces reflejan las relaciones entre los nodos.
Acíclico == sin ciclos dirigidos. En el contexto de los gráficos, este adjetivo significa que al comenzar un camino desde un punto, no recorremos todo el diagrama del gráfico, sino solo una parte. (Es decir, por ejemplo, si comenzamos desde el nodo 2 en la imagen, definitivamente no llegaremos al nodo 1).
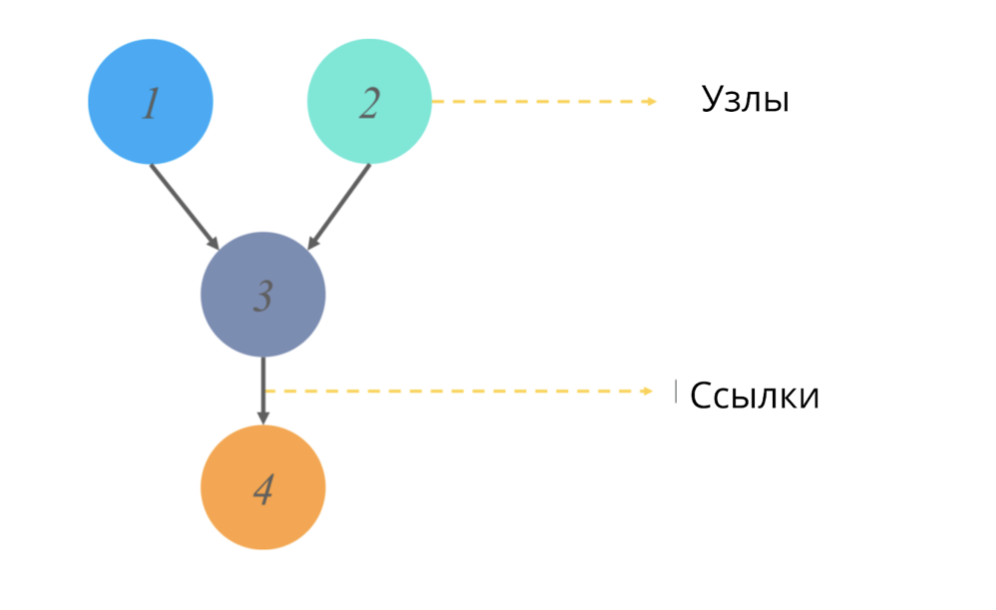
¿Qué simulan estos gráficos y qué valor de salida dan?
Los modelos de gráficos dirigidos inciertos también se basan en un cambio en el origen probabilístico de un evento para cada uno de los valores aleatorios. Una tabla de probabilidad condicional es aplicable para representar e interpretar cada valor y, por lo tanto, podemos simular la ramificación de la probabilidad de eventos secuenciales.
Todo bien. También me confundí al principio. Para una mejor comprensión, analicemos el componente matemático de las redes bayesianas.
Bayesian Network Mathematics
Como ya se mencionó en la definición, las redes bayesianas se basan en la teoría de la probabilidad, por lo tanto, antes de comenzar a trabajar con redes bayesianas, se deben abordar dos preguntas:
¿Qué es la probabilidad condicional?
¿Cuál es la distribución de probabilidad media conjunta?
Probabilidad
condicional La probabilidad condicional de algún evento X es el valor numérico de la probabilidad de que ocurra un evento X, siempre que algún evento Y ya haya ocurrido.
La fórmula de probabilidad estándar para un valor (no dada en el artículo): P (X) = n (x) / N, donde n son los eventos bajo investigación y N son todos los eventos posibles.
Para dos valores, se aplican las siguientes fórmulas:
Si X e Y son eventos dependientes:
P (X o Y) = P (X ⋂ Y) / P (Y), la intersección de la probabilidad de X e Y / para la probabilidad Y. (El signo "" en el numerador significa la intersección de probabilidades)
Si los eventos X e Y son independientes:
P (X o Y) = P (X), es decir, la ocurrencia de los eventos en estudio es igualmente probable entre sí.
Probabilidad conjunta La probabilidad
conjunta es la definición de una medida estadística para dos o más eventos que ocurren al mismo tiempo. Es decir, los eventos X, Y y, supongamos que C ocurren juntos y reflejamos su probabilidad acumulativa usando el valor P (X ⋂ Y ⋂ C).
¿Cómo funciona esto en las redes bayesianas? Veamos un ejemplo.
Un ejemplo que refleja la esencia de la red bayesiana.
Digamos que necesitamos modelar la probabilidad de obtener una de las calificaciones de un estudiante en un examen.
La puntuación está compuesta por:
- Nivel de dificultad del examen (e): variable discreta con dos gradaciones (difícil, fácil)
- IQ del alumno: variable discreta con dos gradaciones (baja, alta)
El valor de evaluación resultante se usará como un predictor (valor predictivo) de la probabilidad de que un estudiante o una estudiante ingrese a la universidad.
Sin embargo, la variable IQ también afectará la admisión a la admisión.
Representamos todos los valores utilizando un gráfico acíclico dirigido y una tabla de distribución de probabilidad condicional.
Usando esta representación, podemos calcular alguna probabilidad acumulativa, formada a partir del producto de las probabilidades condicionales de cinco variables.
Probabilidad acumulada:
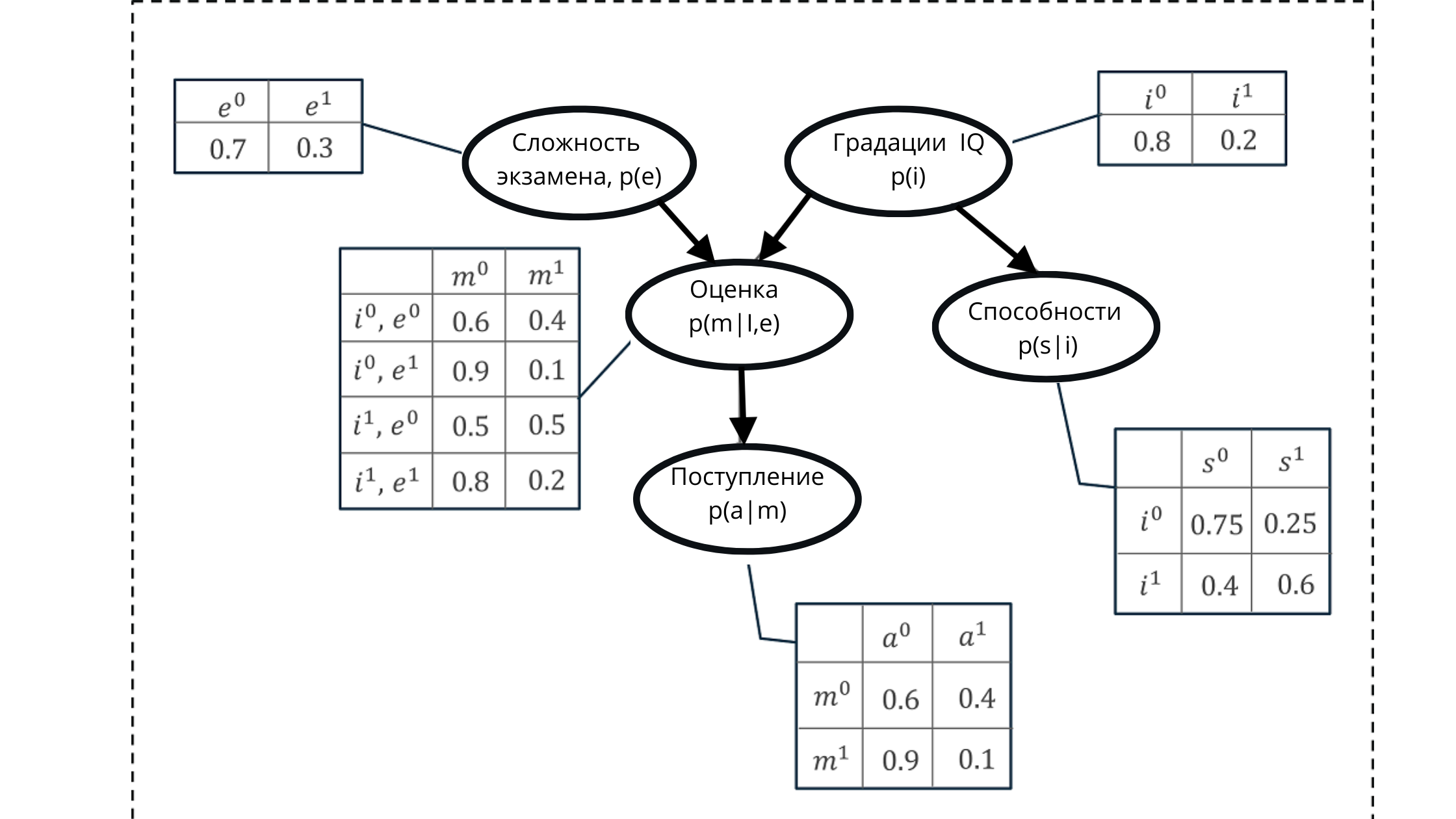
En la ilustración:
p (e) es la distribución de probabilidad para las calificaciones de la variable del examen (afecta la calificación p (m | i, e)))
p (i) es la distribución de probabilidad para las calificaciones de la variable IQ (afecta la calificación p (m | i, e )))
p (m | i, e) - distribución de probabilidad para las calificaciones, basada en el nivel de CI y la dificultad del examen (depende de p (i) y p (e))
p (s | i) - coeficientes de probabilidad para las habilidades de los estudiantes , basado en el nivel de su IQ (depende de la variable IQ p (i))
p (a | m) es la probabilidad de admisión de un estudiante a la universidad, según sus estimaciones p (m | i, e)
Aquí, recuerdo que la propiedad de un gráfico acíclico es un reflejo relación. En la figura, podemos ver claramente cómo los nodos padres afectan a los niños y cómo los niños dependen de los padres.
De ahí surge la formulación del conjunto de valores generados utilizando redes bayesianas.
La esencia de la red bayesiana
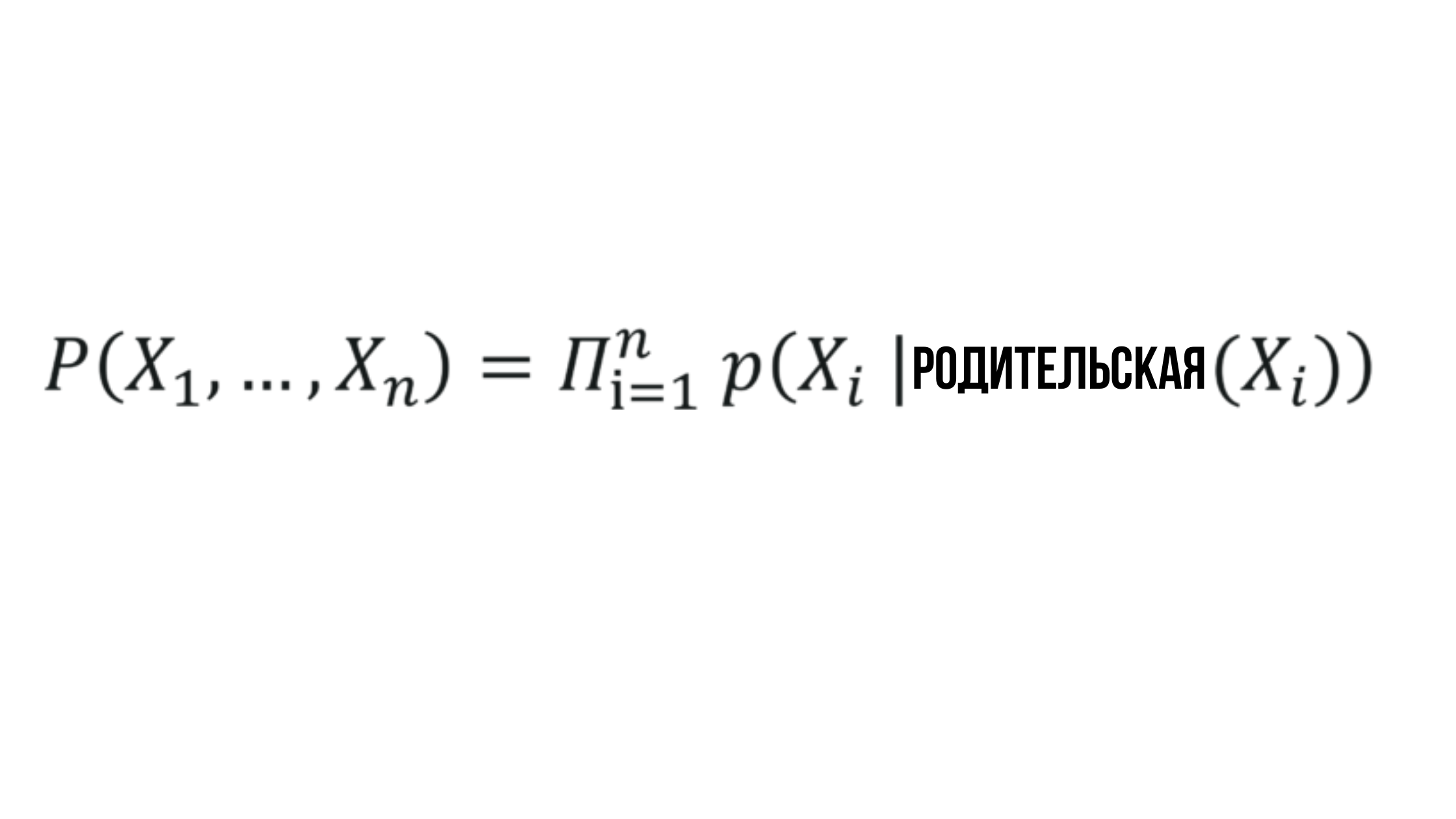
Donde la probabilidad X_i depende de la probabilidad del nodo padre correspondiente y puede representarse por cualquier valor aleatorio.
Suena simple, y con razón: las redes bayesianas son uno de los métodos más simples utilizados en el análisis descriptivo, el modelo predictivo y más.
Red Bayesiana en Python
Veamos cómo aplicar una red bayesiana a un problema llamado la paradoja de Monty Hall.
El resultado final: imagina que eres un participante en el formato de actualización del juego "Field of Miracles". El tambor ya no gira; ahora no debes aplicar tu F, sino jugar con p.
Hay tres puertas frente a usted, detrás de las cuales es igualmente probable que se ubique un automóvil. Las puertas, detrás de las cuales no hay automóvil, lo llevarán a las cabras.
Después de elegir, el líder del resto abre el que lleva a la cabra (por ejemplo, usted eligió la puerta 1, lo que significa que el líder abre las puertas 2 o 3) y lo invita a cambiar su elección.
Pregunta: que hacer
Solución: inicialmente la probabilidad de elegir una puerta con un automóvil = 33%, y con una cabra = 66%.
- Si alcanza el 33%, cambiar la puerta conduce a una pérdida => posibilidad de ganar == 33%
- Si alcanza el 66%, el cambio conduce a una ganancia => probabilidad de ganar == 66%
Desde el punto de vista de la lógica matemática, cambiar la puerta en conjunto lleva a una victoria en el 66% del porcentaje y a una pérdida en el 33%. Por lo tanto, la estrategia correcta es cambiar la puerta.
Pero estamos hablando de la red aquí, y puede haber muchas puertas, por lo que transferiremos la solución al modelo.
Construyamos un gráfico acíclico dirigido con tres nodos:
- Premio puerta (siempre con un auto)
- Puerta seleccionable (ya sea con un automóvil o con una cabra)
- Puerta que se puede abrir en el evento 1 (siempre con una cabra)
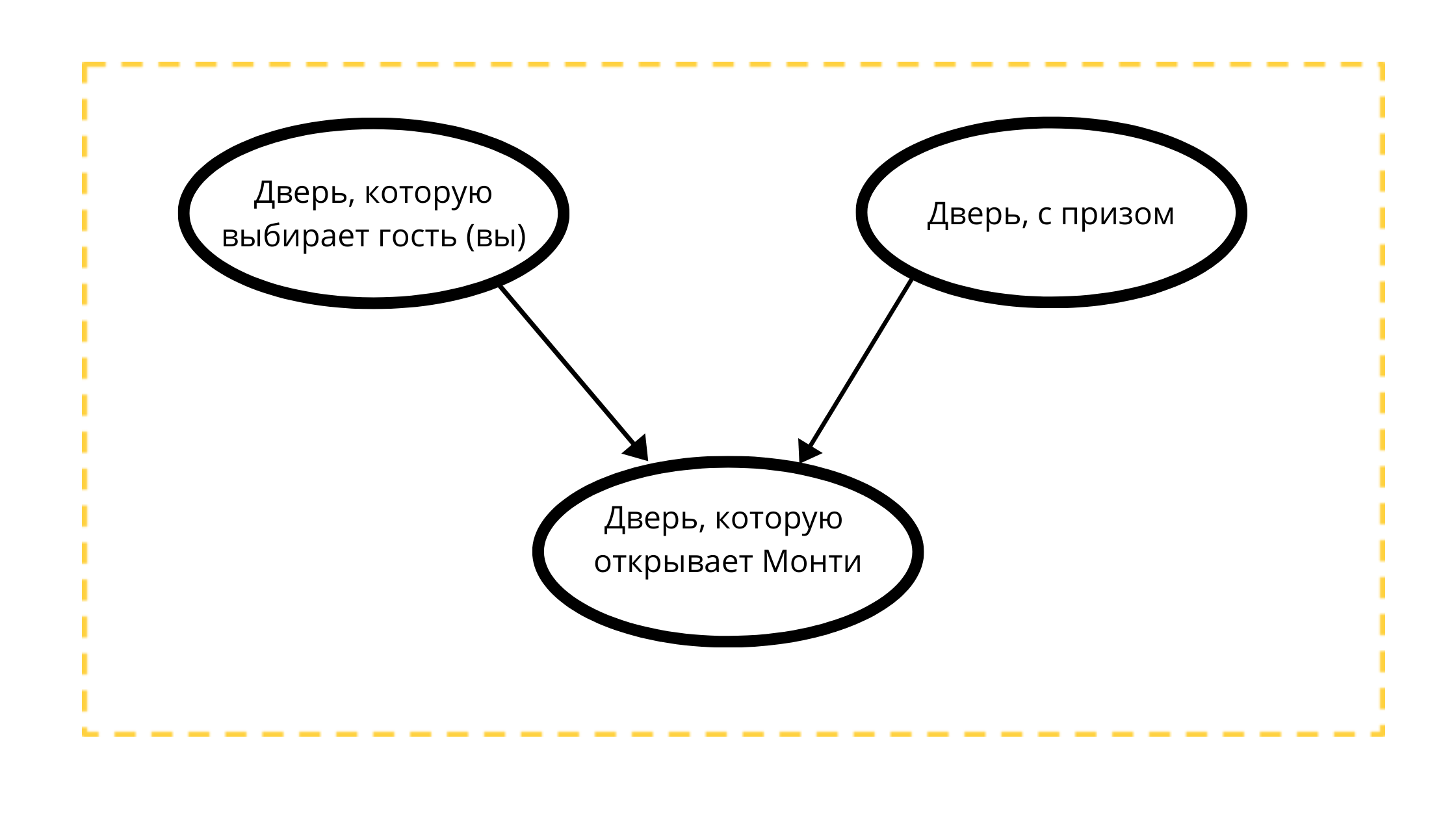
Lectura del recuento:
la puerta que Monty abrirá está estrictamente influenciada por dos variables:
- La puerta elegida por el invitado (usted) tk Monti 100% NO abrirá su elección
- Una puerta con un premio, tal vez Monty siempre abre una puerta sin premio.
De acuerdo con las condiciones matemáticas del ejemplo clásico, el premio puede ubicarse igualmente detrás de cualquiera de las puertas, así como también es probable que elija cualquier puerta.
#
import math
from pomegranate import *
# " " ( 3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# " " ( )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# , ,
#
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
#
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()En el fragmento los valores son:
- A - la puerta elegida por el huésped
- B - puerta de premio
- C - puerta elegida por Monty
En el fragmento, calculamos el valor de probabilidad para cada uno de los nodos del gráfico. Los dos nodos superiores obedecen en nuestro ejemplo una distribución de probabilidad igual, y el tercero refleja la distribución dependiente. Por lo tanto, para no perder valor, las probabilidades de cada una de las combinaciones posibles del juego se calculan para .
Una vez preparados los datos, creamos una red bayesiana.
Es importante tener en cuenta aquí que una de las propiedades de dicha red es revelar la influencia de las variables ocultas en los observables. Al mismo tiempo, ni las variables ocultas ni las observables deben especificarse o determinarse de antemano: el modelo mismo examina la influencia de las variables ocultas y lo hará con mayor precisión cuanto más variables reciba.
Comencemos a hacer predicciones.
beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}Analicemos el fragmento usando el ejemplo de la variable A.
Supongamos que el invitado lo eligió (A).
El evento “hay un premio detrás de la puerta” en la etapa de elegir una puerta por un invitado tiene una distribución de probabilidad == ⅓ (ya que cada puerta puede ser igualmente probable que sea un premio).
Luego, agregue el valor de las probabilidades de que la puerta sea el premio en la etapa en que Monty elige la puerta. Dado que no sabemos si la puerta del premio fue excluida por nuestra propia elección (invitado) en el paso 1, la probabilidad de que la puerta sea un premio en esta etapa es 50/50
beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
En este paso, modificaremos los valores de entrada para nuestra red. Ahora funciona con la distribución de probabilidad obtenida en los pasos 1 y 2, donde
- Las posibilidades de ganar en la puerta de nuestra elección no han cambiado (33%)
- las posibilidades de ganar el premio en la puerta abierta por Monty (B) han sido canceladas
- las posibilidades de ser un premio en la puerta, que se dejó desatendido, tomaron el valor 66%
Por lo tanto, como se concluyó anteriormente, la estrategia correcta por parte de los invitados para este juego es cambiar la puerta: aquellos que cambian la puerta matemáticamente tienen ⅔ posibilidades de ganar contra aquellos que no cambiarán la puerta (⅓).
En el ejemplo con tres nodos, los cálculos manuales son indudablemente suficientes, pero con un aumento en el número de variables, nodos y factores influyentes, la red bayesiana puede resolver el problema del valor predictivo.
Aplicación de redes bayesianas
1. Diagnóstico:
- predicción de enfermedad basada en síntomas
- modelado de síntomas para la enfermedad subyacente
2. Buscando en Internet:
- formación de resultados de búsqueda basados en el análisis del contexto del usuario (intenciones)
3. Clasificación de documentos:
- filtros de spam basados en análisis de contexto
- distribución de documentación por categoría / clase
4. Ingeniería genética.
- modelando el comportamiento de las redes de regulación génica basadas en las interconexiones y relaciones de segmentos de ADN
5. Productos farmacéuticos:
- Monitoreo y valor predictivo de dosis aceptables
Los ejemplos anteriores son hechos. Para una comprensión completa, es relevante imaginar en qué etapa está conectada la creación de una red bayesiana y en qué nodos consiste el gráfico que la describe.
El problema de la paradoja de Monty Hall es solo una base que le permite a uno "señalar con el dedo" ilustrar el funcionamiento de las cadenas basadas en una combinación de distribuciones de probabilidad dependientes e independientes. Espero haberlo entendido.
PD: No soy un as de Python y solo estoy aprendiendo, así que no puedo ser responsable del código del autor. La publicación de este artículo sobre Habré persigue una mayor liberación en el mundo del trabajo intelectual de traducción. Creo que en el futuro podré generar mis propios tutoriales; en ellos ya estaré contento de ver pensamientos constructivos sobre el código.