El modelo matemático del fenómeno postula que todos los procesos tienen lugar en el espacio-tiempo de 4 dimensiones, en el que los fenómenos SRT se derivan de la preservación del intervalo de eventos durante la transformación de la rotación del sistema de coordenadas. Difícilmente se puede negar que la realidad, por así decirlo, se extiende sobre construcciones matemáticas. Además, el hecho de que los números imaginarios, en realidad inimaginables, desempeñen un papel casi completamente importante en ellos, no disminuye el éxito de la ciencia. Incluso E. Mach dijo que las explicaciones son superfluas si los fenómenos observados están bien descritos por fórmulas. Y no discutamos con esta empiriocrítica.
Los matemáticos inventan abstracciones y se las prueban a la realidad. De ahí la singularidad, los agujeros de gusano y otras cosas exóticas. O tal vez valga la pena fantasear , por ejemplo, sobre lo que cambiaría en nuestras ideas sobre el mundo si la causa de la contracción de Lorentz fuera un mecanismo físico hipotéticamente asumido. Por qué no?
1 la causa física de la contracción de Lorentz
Primero, expresaré la máxima aparentemente obvia de que las partículas, los átomos y las moléculas interactúan entre sí a través de campos físicos . Por supuesto, podemos decir que intercambian partículas cuánticas, pero ahora estamos jugando en el campo de la teoría relativista, por lo que por ahora nos olvidaremos de los cuantos. Por lo tanto, la primera suposición fantástica es que es precisamente debido al equilibrio mutuo de los efectos de campo que las partículas se agregan a una determinada configuración y forman cuerpos . Si alguna partícula se desvía de la posición de equilibrio, entonces se producirá una perturbación de campo, que moverá el resto de las partículas, lo que, a su vez, causará un efecto de campo inverso en esta partícula.
Y la segunda suposición es quela perturbación de campo se propaga en un cierto espacio común con una cierta velocidad determinada . Y la naturaleza fantástica de esta suposición es que, según la ciencia, el campo existe por sí mismo en el espacio-tiempo de 4 dimensiones (P-W) y no se extiende sobre nada. En general, es difícil en ciencia ... Asumiremos que los campos se extienden y existen en un solo espacio tridimensional, en el que estamos, la Tierra y las estrellas. Parece que esto es evidente y quién no sabe, pero veamos qué sucede. Aquellos que no estén interesados en molestarse con las fórmulas pueden limitarse a leer solo el texto seleccionado.
Entonces, estamos de acuerdo en que existe un tiempo de interacción entre las partículas, que se compone de la hora de llegada de la indignación a ellos y la hora de devolución de la respuesta de ellos. Como resultado, la configuración previa del cuerpo se establecerá gradualmente nuevamente. Fig.1 Influencias de campo que determinan la posición de la partícula
Para cualquier punto del cuerpo, es posible distinguir grupos de puntos con los que tendrá tiempos de interacción iguales y que llamaremos isócronos con este punto. La situación se refleja en la figura 1. Naturalmente, en reposo, la esfera de cualquier radio de reposo R alrededor de un punto es el lugar geométrico de los puntos (GMT) isócrono con él.
Tenga en cuenta que el movimiento de una partícula en cada momento está determinado por la suma de las fuerzas resultantes que se aplican simultáneamente desde la totalidad de todos los grupos de partículas isócronas con ella.... Tratemos de descubrir cómo cambiará la superficie del GMT, formada por un conjunto de puntos 2, 3, etc., cuando el cuerpo se mueva. con los mismos tiempos de interacción con el punto 1, que ya no puede ser una esfera.
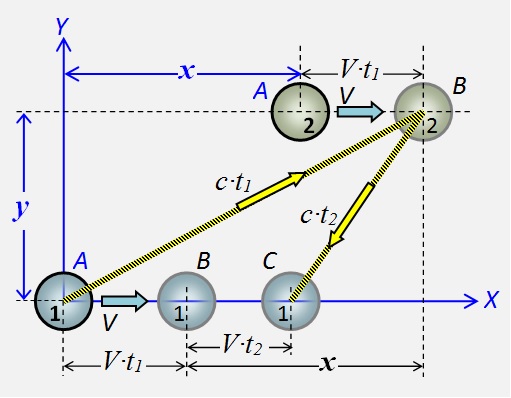Vamos puntos del cuerpo 1 y 2 están fijados mutuamente y de forma sincrónica en movimiento la derecha con velocidad V . Cuando un punto está en el origen, el campo de perturbación se envía al punto 2. La disposición mutua de los puntos marcados con la letra A . Fig.2 Esquema de interacciones de campo de los puntos del cuerpo, de ida y vuelta
Cuando la perturbación alcanza el punto 2, recorrerá la distancia V ∙ t 1 . Posiciones marcadas puntos con la letra B . Durante el tiempo que la perturbación regresa del punto 2 al punto 1, el punto 2 cubrirá la distanciaV ∙ t 2 . Su nueva posición está marcada con el C .
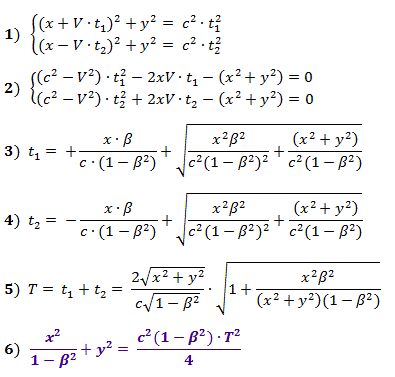Fórmulas (1), de acuerdo con el teorema de Pitágoras, describen las distancias en la Fig. 2, y la obtuvieron a partir de ellos (2) son ecuaciones para el cálculo de los tiempos t 1 y t 2 , los valores de los que se dan por las fórmulas (3) y (4) para los valores positivos de las raíces, donde β = V / c .
La fórmula (5) da el valor del tiempo de interacción desde el envío de una perturbación hasta la recepción de una respuesta.
De (5) obtenemos la ecuación (6) para las coordenadas x e y del lugar geométrico de los puntos isócronos con los cuales el tiempo de interacción del punto 1 es el mismo.
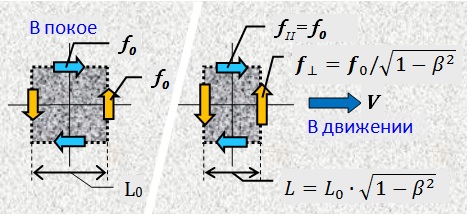
La fórmula (6) describe el elipsoide que se muestra en la Fig. 3, comprimido a lo largo de la dirección del movimiento (a lo largo del eje X) por √ (1 - β 2 ) veces, es decir, de acuerdo con la fórmula de Lorentz. El punto 2 en la superficie de la esfera en reposo, mientras se mueve, se moverá a la posición 2 ' . En este caso, los puntos de material que eran isócronos con el punto 1 en reposo permanecerán isócronos con él durante el movimiento . Fig.3
Entonces, cuando se mueve, un objeto material se comprime de acuerdo con Lorentz precisamente porque la misma "imagen" de los campos físicos está comprimida, lo que garantiza su integridad en el espacio .
Dado que la contracción de Lorentz es la misma para todos los puntos isócronos que rodean cada punto del objeto, entonces todo el objeto en movimiento se contraerá igualmente proporcionalmente a lo largo del eje de movimiento.
2. Derivación de la fórmula para la dilatación del tiempo.
Determinemos el tiempo de interacción cuando el objeto se mueve en comparación con el tiempo de interacción en reposo.
Las fórmulas (7) relacionan las coordenadas de los puntos durante el movimiento con sus coordenadas en reposo de acuerdo con la
ecuación (6). La fórmula (8) calcula el tiempo de interacción en reposo. Fórmulas (9) y (10) se obtuvieron de la fórmula (6) sustituyendo en ella los valores de las coordenadas x y y y R de resto de las fórmulas (7). La fórmula (11) es equivalente a (10). La fórmula (12), obtenida de (11) al sustituir el lado izquierdo de la fórmula (8) en ella, conecta los tiempos de interacción en reposo y durante el movimiento. En la forma tradicional, esto se refleja en la fórmula (13), donde T 0 es el intervalo de tiempo entre eventos en un objeto en reposo, yT es el intervalo de tiempo entre los mismos eventos en un cuerpo en movimiento.
Por lo tanto, los tiempos de interacción de todos los puntos en un objeto en movimiento aumentan en la misma proporción según Lorentz en comparación con el tiempo de interacción en reposo. En consecuencia, en general, todos los procesos en un objeto en movimiento en realidad se ralentizan en el mismo aspecto .
La razón de la desaceleración del tiempo es fácil de entender si tenemos en cuenta que la perturbación del campo desde la parte posterior de las partículas que interactúan tendrá que alcanzar a la delantera en la dirección del movimiento . Cuando la velocidad del cuerpo es casi igual a la velocidad de la luz, tomará mucho tiempo alcanzarla, y si la velocidad del cuerpo es igual a la velocidad de la luz, nunca se pondrá al día. Todos los cambios en el cuerpo se detendrán y el tiempo en él parecerá detenerse.
3. Explicación del fenómeno de la constancia de la velocidad de la luz, etc.
Hagamos un experimento mental. Deje que se emita un pulso de luz desde el último vagón del tren, que se recibe en su vagón principal. Tenemos que medir el tiempo T 0 que la luz pasará en el paso de un tren de longitud conocida L 0 en su propio sistema. En la prueba, utilizaremos los supuestos sobre la homogeneidad e isotropía del espacio, en particular, asumiremos los mismos resultados de medición para la primera y segunda mitad del tren, así como para las direcciones hacia adelante y hacia atrás. Pero, estrictamente hablando, estos supuestos son válidos solo dentro de la ubicación y el tiempo del experimento.
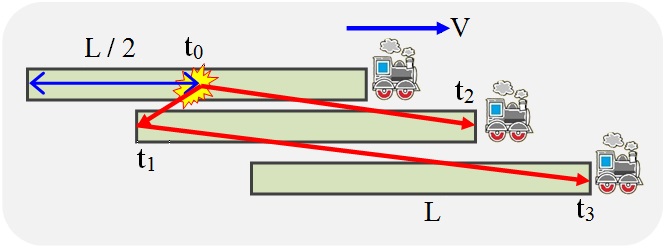
Fig.4. Pensamiento experimental para determinar la velocidad de la luz en un tren en movimiento
Para sincronizar el momento de enviar una señal desde el último vagón del tren y el inicio del contador de tiempo en su vagón delantero, usamos un pulso de luz de inicio desde el medio del tren a ambos extremos.
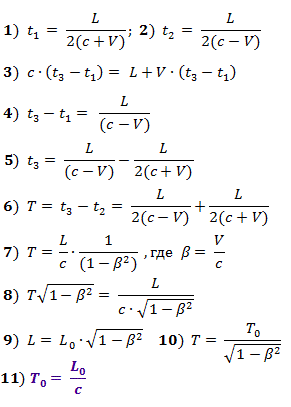
Cuando la señal de arranque desde el medio del tren alcanza su cola (tiempo t 1 ), se enviará un pulso de luz. Cuando la señal de inicio llega a la cabeza del tren (tiempo t 2 ), la cuenta regresiva comenzará hasta la llegada del pulso enviado.
Cuando la luz viaja a la cola, su velocidad se suma a la velocidad del tren; cuando a la cabeza, la velocidad del tren se resta. Obtenemos las relaciones que figuran a continuación en las fórmulas (1) - (6).
Tiempo T = t 3 - t 2 es el intervalo de tiempo, que,Según el observador en el tren , separa los eventos del momento de enviar la señal desde el final del tren (desde el momento de recibir la señal de inicio allí) y el momento de su recepción en la cabeza del tren.
De (6) obtenemos la fórmula (7), que transformamos a la forma (8). Además, tendremos en cuenta que todas las cantidades L , T y t aquí se miden en el marco de referencia de un observador externo en el espacio donde se está llevando a cabo el experimento mental. Pero cuando un objeto se mueve en el espacio, su longitud, como se demostró en el Capítulo 1 , en realidad sufre una contracción de Lorentz, y los tiempos de los eventos, como se demostró en el Capítulo 2, en realidad se ralentiza la misma cantidad de veces, es decir proceder más tiempo que en reposo, lo que se refleja en las fórmulas (9) y (10). Sustituyendo estas proporciones en la fórmula (8) por el intervalo T - el tiempo de viaje de la luz desde la cola hasta la cabeza del tren, obtenemos la relación (11).
Pero, ¿qué relación tienen estos T 0 y L 0 en reposo con su propio tiempo y duración para los mismos eventos, medidos en el marco de referencia inercial (IRF) asociado con un tren en movimiento? Obviamente son su igual . El hecho es que el tiempo y la duración se expresan numéricamente a través de su relación con los estándares. En consecuencia, las mediciones de las coordenadas temporales y espaciales de algo hecho en reposo serán numéricamenteson iguales a las mediciones de la misma, realizadas en un ISO en movimiento, ya que al mover los valores de las mediciones y los estándares cambiarán proporcionalmente.
La pregunta es cómo cambian exactamente cuando se mueven en el espacio. Un experimento mental con un tren demuestra que cambian de tal manera que el valor numérico de la velocidad de la luz medida en IFR permanece igual al valor de su velocidad en el espacio . Esto es precisamente lo que no era a priori una prueba obvia y requerida.
Vemos que el "postulado de la constancia de la velocidad de la luz" se deriva solo del hecho de la contracción de Lorentz, que se deriva matemáticamente de la dependencia de la ubicación de la materia material en la velocidad de propagación y configuración de los campos físicos en el espacio .
Para completar la imagen, también definimos la velocidad de la luz a través del movimiento del tren, por ejemplo, entre las paredes del vagón a una distancia S 0 entre sí. Para hacer esto, medimos el tiempo de movimiento del pulso de luz ( 2 · t 0 ) hacia adelante y hacia atrás. En vista de la simetría obvia de "allí" y "atrás", consideraremos solo "allí". En el sistema de un observador externo, el movimiento en el espacio ocurre como se muestra en la figura 5.
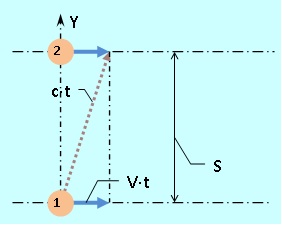Por lo tanto, tenemos (c · t) 2 = S 2 + (V · t) 2 , de donde obtenemos t = S / (c · √ (1 - β²)) , donde β = V / c .
En el sistema de trenes, el tiempo apropiado transcurrido t 0conectado con el tiempo transcurrido en el espacio por la relación t = t 0 / (√ (1 - β²)) . Sustituyendo esta expresión en la fórmula para t en el espacio, obtenemos t 0 = S / c .
Fig.5. Experimento de pensamiento para determinar la velocidad de la luz en un tren en movimiento /
En el propio sistema del tren para el mismo t 0, tenemos la relación t 0 = S 0 / c 0 . Pero dado que las dimensiones transversales no cambian durante el movimiento, es decir S = S 0 , obtenemos que c 0 = c .
Supongo que no hay necesidad de probar la constancia de la velocidad medida de la luz para una orientación arbitraria del haz, lo que solo agregaría una complejidad innecesaria. Considerando la probada invariancia de la velocidad de la luz, es fácil derivar las transformaciones de Lorentz (L), y sin ninguna apelación a las ecuaciones de Maxwell o al espacio matemáticamente abstracto de Minkowski.
4. Derivación de las transformaciones de Lorentz.
El evento consiste en la llegada de un pulso de luz en el punto " E ",
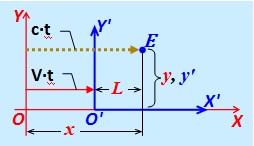ubicado en las coordenadas sin cambios x ' e y' en el sistema de referencia {X ', Y'}, moviéndose con una velocidad V relativa al IFR fijo {X, Y}, enviado en el momento en que los puntos O y O 'de ambos CO coincidieron. Fig.6.
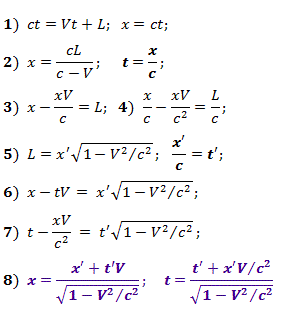En su propia longitud CO {X ', Y'} L , medida en CO {X, Y}, la coordenada x ' corresponderá . Para el evento, el sistema de ecuaciones (1) es válido, resolviendo lo que obtenemos (2), y luego (3) y (4).
Dado que las longitudes de los cuerpos en movimiento se comprimen de acuerdo con Lorentz, y la velocidad de la luz, como se demostró en el Capítulo 3 , es la misma en cualquier FR, entonces para x ' apropiadoyt ' en {X', Y '} las relaciones (5) son válidas. Sustituyendo las relaciones de (5) en (3) obtenemos (6), y sustituyéndolas en (4), obtenemos (7). En virtud de la relatividad del movimiento, podemos considerar el sistema en movimiento {X, Y}, pero luego en (6) y (7) es necesario reemplazar las variables no sombreadas con las sombreadas, y la velocidad V debe tomarse con el signo opuesto, o simplemente resolver el sistema con respecto a x y t .
Como resultado, obtenemos expresiones (8) para la forma canónica de transformaciones de Lorentz de coordenadas y tiempo de eventos en diferentes IFR.
Cuando se usa PL como un método matemático puramente formal, el mecanismo físico de los fenómenos SRT permanece inmanifiesto. Por lo tanto, en mis artículos anteriores sobre el efecto Doppler relativistayLas aberraciones de luz , así como las leyes de reflexión de un espejo inclinado en movimiento , SL no se utilizaron en principio para demostrar las razones físicas de estos fenómenos.
5. Justificación del principio de relatividad y limitaciones de su aplicabilidad.
Tenga en cuenta que si en reposo en el diagrama de la Fig. 1, la perturbación desde el punto 1 hasta el GMT de los puntos isócronos se produjo simultáneamente, entonces durante el movimiento, en el diagrama de la Fig. 2, esto ya no se cumple. En cada punto de este GMT, la respuesta a la perturbación se creará en diferentes momentos, pero convergerán en el punto 1 simultáneamente . La pregunta es, ¿el resultado será el mismo que en reposo?
Se demostró anteriormente que en cualquier IFR los tiempos y distancias adecuados medidos entre todos los puntos serán los mismos que en reposo . En consecuencia, el número de períodos, por ejemplo, iniciadosLa onda electromagnética entre cualquier punto será la misma que en reposo. Dado que la perturbación de un campo de una configuración arbitraria puede representarse mediante una expansión en una serie de armónicos monocromáticos, las configuraciones e intensidades de todos los campos en el sistema intrínseco serán las mismas en reposo, respectivamente. En consecuencia, no se violan las relaciones de fase y la sincronización de los campos que forman el cuerpo, y todos los procesos en él procederán como durante el reposo.
Esto es exactamente lo que proclama el "principio de relatividad" de Einstein, y, como vemos, matemáticamente se deduce inevitablemente de dos supuestos (ver Capítulo 1), permítanme recordarles: primero : que la posición de las partículas reales está determinada por la estructura de los campos , y segundo , queLa propagación de campo ocurre a una velocidad finita .
Es decir, el principio de la relatividad ya no es, a priori, un principio universal , sino una consecuencia, y tiene límites claros de aplicabilidad . En particular, la velocidad de la luz no tiene el significado de una constante mundial, sino que es una velocidad específica de la luz en una región específica del espacio . Y en algunos lugares puede ser diferente debido a la interacción con los campos físicos locales, por ejemplo, la gravedad. Entonces, tenemos dos alternativas que resultan en exactamente las mismas fórmulas relativistas:
- primero, ortodoxo y científico: requiere postular a priori un verdadero principio de relatividad ;
- : ,
En el primer caso, los fenómenos de SRT no requieren explicación, y sus causas y mecanismos permanecen desconocidos. La pregunta "¿Por qué?" incluso resulta estar fuera de la ciencia.
En el segundo , los supuestos son incluso bastante lógicos y no se requiere nada para postular, y son "fantásticos" solo en la medida en que otras razones para el relativismo sean aceptadas en la ciencia. A la pregunta "¿por qué los fenómenos SRT son así?" aquí se da una explicación clara e incluso casi trivial. Pero existe una necesidad urgente de descubrir la naturaleza de la materia y en qué relación se encuentra con los campos físicos.
Por lo tanto, seguiremos fantaseando más.
6. Derivación de la fórmula E = Mc² y las ecuaciones de dinámica.
Primero, descubramos cómo se transforman las fuerzas a velocidades relativistas. Seleccionemos el elemento de volumen en el cuerpo sobre el que actúan los momentos equilibrados de fuerzas. Cuando el cuerpo se mueve, el tamaño longitudinal (a lo largo de la trayectoria de movimiento) del elemento seleccionado
disminuirá de acuerdo con el coeficiente de Lorentz. Para que el elemento permanezca en equilibrio, las fuerzas perpendiculares al movimiento deben aumentar exactamente en la misma proporción. Fig.7.
La magnitud de las fuerzas paralelas al movimiento no cambiará. El factor de dependencia de las fuerzas con respecto a la orientación con respecto a la dirección del movimiento debe tenerse en cuenta en la expansión del vector de fuerzas en las siguientes fórmulas.
Tenga en cuenta que la aceleración del cuerpo a una cierta velocidad se lleva a cabo por la fuerza aplicada, que, en consecuencia, hace algo de trabajo, lo que aumenta la energía del cuerpo. Y¿Cuál es la diferencia entre un cuerpo disperso en el espacio y un cuerpo en reposo? El hecho de que el overclockeado se comprime de acuerdo con Lorentz . En el Capítulo 1, se deriva una fórmula para el locus de puntos (GMT) que rodea un punto dado, desde el cual tienen el mismo tiempo de interacción de los campos físicos. Este GMT resulta ser un elipsoide comprimido según Lorentz en la dirección del movimiento. Ahora prestemos atención al hecho de que el volumen W de este elipsoide disminuye en proporción a la contracción de Lorentz. Esto se refleja en la fórmula (1) a continuación. Ahora hagamos una suposición realmente fantástica de que cuando un cuerpo se acelera, el trabajo de fuerza se gasta en comprimir el volumen de espacio que ocupa, que luego permanece sin cambios en el movimiento libre. Al menos, esta suposición no es peor que la máxima científica de que el espacio puede doblarse o hincharse.
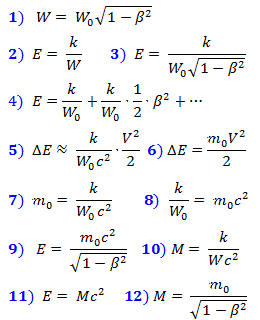Suponga que esta energía E es inversamente proporcional al volumen al que fue posible comprimirla de acuerdo con la fórmula (2) o (3) después de sustituir (1) en ella. Expandimos
E desde (3) a una serie de Taylor (4), donde (5) es el incremento de energía desde la velocidad en la primera aproximación a bajas velocidades. Pero a bajas velocidades también es igual a (6). Comparando (5) y (6), obtenemos (7) y (8). Sustituyendo (8) en (3), obtenemos (9), que conecta la energía de un cuerpo en el espacio comprimido con su masa en reposo.
Expresemos la masa relativista mediante la fórmula (10), de donde, sustituyendo (2), obtenemos la conocida expresión (11), que relaciona masa y energía. Comparando (9) y (11), obtenemos (12).
La masa es solo otra formulación de la energía gastada en el espacio de compresión. Y en este sentido son equivalentes. Y la sustancia solo "marca" el área de espacio ocupada por el cuerpo.
Cambio en la energía total E del sistema, es decir La energía de compresión del espacio, de acuerdo con la mecánica clásica newtoniana, es igual al trabajo de la fuerza aplicada como producto de la fuerza por trayectoria, y el cambio en el momento P del sistema es igual al producto de la misma fuerza y el tiempo de su acción. Estas dependencias se reflejan en las fórmulas (13). Después de sustituir en ellos las expresiones para la energía de (11) y el impulso Pde la fórmula (14)
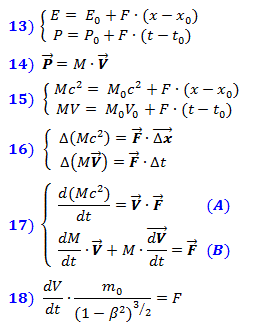obtenemos el sistema de ecuaciones (15), que se escribe en forma de pequeños incrementos en (16) en forma de vector. Luego, diferenciando con respecto al tiempo, escribimos el sistema de ecuaciones diferenciales (17) que describe la dinámica relativista. No es necesario diferenciar la fuerza F , ya que es externa y no depende de las variaciones de las variables del sistema. Sustituyendo la expresión de masa de (12) en la fórmula ( A ), obtenemos la conocida fórmula relativista para el movimiento rectilíneo (18). 
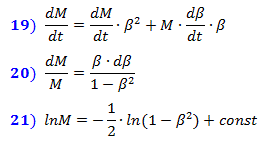Del sistema de ecuaciones (17) es posible descubrir la dependencia de la masa de la velocidad. Sustituyendo F de la fórmula ( B ) en la fórmula ( A ) y dividiendo ambos lados de la igualdad por c², al acelerar a lo largo de la trayectoria del movimiento, obtenemos las expresiones (19) y (20). De donde, integrando, obtenemos la expresión (21). Es fácil ver que es equivalente a la expresión logarítmica (12) para la masa relativista, donde const es igual al logaritmo de la masa en reposo m 0 . Esto significa que tal dependencia de la masa de la velocidad asegura la correspondencia de la energía Mc² y el momento M · V , en las fórmulas (16, 17). Y a partir de aquí también se deduce que el valor que previamente asumimos como la masa en reposo es una constante independiente de la velocidad, como está escrito en las fórmulas originales (9). Y eso significa que nuestra suposición sobre la dependencia de la energía en el grado de compresión espacial es correcta.
Por supuesto, la afirmación de compresión espacial no es muy convincente. Si se supone que el espacio es un contenedor vacío de partículas y cuerpos, ¿cómo se puede comprimir el vacío? El vacío seguirá siendo el vacío. Sin embargo, la ciencia se permite hablar sobre la curvatura del espacio vacío: las fórmulas lo requieren. Sin embargo, estrictamente hablando, su espacio es una abstracción matemática.
Pero podemos suponer razonablemente que el espacio no está vacío, sino que está lleno de algo que, supongamos, no en un estado comprimido, es percibido por nosotros como un vacío.... Cuando, por ejemplo, está bajo tensión de compresión, tenemos partículas y cuerpos materiales. Cuando estos están en reposo en él, el grado de compresión (energía) de una sección de esta materia corresponde a la masa en reposo del cuerpo, y con su aceleración, tanto el grado de compresión (energía) del cuerpo como el aumento de masa correspondiente.
Y en este entorno material, los campos físicos que determinan la ubicación y la interacción de las partículas (hasta los "muy, muy" primarios, que, seguimos fantaseando , resultarán ser el fenómeno de enfocar campos desde su entorno sin los cuales no existen), pueden existir y propagarse a una velocidad específica ), cuya energía de reposo y movimiento está determinada por el grado de compresión del área de materia primaria ocupada por ellos . Realmente,Las ecuaciones de la dinámica relativista solo describen el movimiento de estas inhomogeneidades de estrés (cuerpos materiales) en la materia prima . Como pudimos ver, no hay contradicciones con el experimento de Michelson y las transformaciones de Lorentz.