
Fuente: unsplash.com El
tres veces campeón mundial de Fórmula 1 Jackie Stewart dice que comprender el auto lo ayudó a convertirse en un mejor conductor: "Un piloto no tiene que ser ingeniero, sino un interés en la mecánica ".
Martin Thompson (creador de LMAX Disruptor ) aplicó este concepto a la programación. En pocas palabras, comprender el hardware subyacente mejorará sus habilidades a la hora de diseñar algoritmos, estructuras de datos, etc.
El equipo de Mail.ru Cloud Solutions tradujo un artículo que profundizó en el diseño del procesador y analizó cómo comprender algunos de los conceptos de CPU puede ayudarlo a tomar mejores decisiones.
Los basicos
Los procesadores modernos se basan en el concepto de multiprocesamiento simétrico (SMP). Un procesador está diseñado de tal manera que dos o más núcleos comparten una memoria común (también llamada memoria de acceso principal o aleatorio).
Además, para acelerar el acceso a la memoria, el procesador tiene varios niveles de caché: L1, L2 y L3. La arquitectura exacta depende del fabricante, modelo de CPU y otros factores. Sin embargo, la mayoría de las veces, los cachés L1 y L2 operan localmente para cada núcleo, mientras que L3 se comparte en todos los núcleos.

Arquitectura SMP
Cuanto más cerca esté la memoria caché del núcleo del procesador, menor será la latencia de acceso y el tamaño de la memoria caché:
| Cache | Retrasar | Ciclos de CPU | El tamaño |
| L1 | ~ 1.2 ns | ~ 4 | Entre 32 y 512 KB |
| L2 | ~ 3 ns | ~ 10 | Entre 128 KB y 24 MB |
| L3 | ~ 12 ns | ~ 40 | Entre 2 y 32 MB |
Nuevamente, los números exactos dependen del modelo del procesador. Para una estimación aproximada, si el acceso a la memoria principal tarda 60 ns, el acceso a L1 es aproximadamente 50 veces más rápido.
En el mundo del procesador, existe un concepto importante de localidad de enlace . Cuando el procesador accede a una ubicación de memoria específica, es muy probable que:
- Se referirá a la misma ubicación de memoria en un futuro próximo: este es el principio de la localidad horaria .
- Se referirá a las celdas de memoria ubicadas cerca: este es el principio de localidad por distancia .
La localidad horaria es una de las razones de los cachés de la CPU. ¿Pero cómo usas la localidad a distancia? Solución: en lugar de copiar una celda de memoria en los cachés de la CPU, la línea de caché se copia allí. Una línea de caché es un segmento contiguo de memoria.
El tamaño de la línea de caché depende del nivel de caché (y nuevamente del modelo de procesador). Por ejemplo, aquí está el tamaño de la línea de caché L1 en mi máquina:
$ sysctl -a | grep cacheline
hw.cachelinesize: 64
En lugar de copiar una sola variable en el caché L1, el procesador copia allí un segmento contiguo de 64 bytes. Por ejemplo, en lugar de copiar un solo elemento int64 de un segmento Go, copia ese elemento más siete elementos más int64.
Usos específicos para líneas de caché en Go
Veamos un ejemplo concreto que demuestra los beneficios de los cachés de procesador. En el siguiente código, agregamos dos matrices cuadradas de elementos int64:
func BenchmarkMatrixCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
}
}
}
}
Si es
matrixLengthigual a 64k, produce el siguiente resultado:
BenchmarkMatrixSimpleCombination-64000 8 130724158 ns/op
Ahora, en cambio,
matrixB[i][j]agregaremos matrixB[j][i]:
func BenchmarkMatrixReversedCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
}
}
}
}
¿Esto afectará los resultados?
BenchmarkMatrixCombination-64000 8 130724158 ns/op
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
¡Sí, y radicalmente! ¿Cómo se puede explicar esto?
Tratemos de dibujar lo que está sucediendo. El círculo azul indica la primera matriz y el círculo rosa indica la segunda. Cuando establecemos
matrixA[i][j] = matrixA[i][j] + matrixB[j][i], el puntero azul está en la posición (4.0) y el rosa está en la posición (0.4):
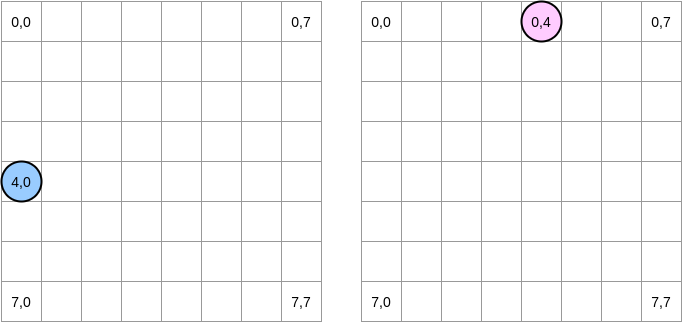
Nota . En este diagrama, las matrices se presentan en forma matemática: con una abscisa y una ordenada, y la posición (0,0) está en el cuadrado superior izquierdo. En la memoria, todas las filas de la matriz están ordenadas secuencialmente. Sin embargo, en aras de la claridad, echemos un vistazo a la representación matemática. Además, en los siguientes ejemplos, el tamaño de la matriz es un múltiplo del tamaño de la línea de caché. Por lo tanto, la línea de caché no se "pondrá al día" en la siguiente fila. Suena complicado, pero los ejemplos aclararán todo.
¿Cómo vamos a iterar sobre las matrices? El puntero azul se mueve hacia la derecha hasta llegar a la última columna y luego se mueve a la siguiente fila en la posición (5,0), y así sucesivamente. Por el contrario, el puntero rosado se mueve hacia abajo y luego se mueve a la siguiente columna.
Cuando el puntero rosado alcanza la posición (0.4), el procesador almacena en caché la línea completa (en nuestro ejemplo, el tamaño de la línea de caché es de cuatro elementos). Entonces, cuando el puntero rosado alcanza la posición (0.5), podemos suponer que la variable ya está presente en L1, ¿verdad?
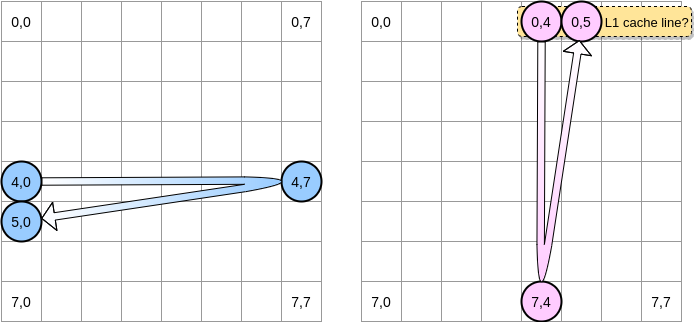
La respuesta depende del tamaño de la matriz :
- Si la matriz es lo suficientemente pequeña en comparación con el tamaño de L1, entonces sí, el elemento (0.5) ya estará en caché.
- De lo contrario, la línea de caché se eliminará de L1 antes de que el puntero alcance la posición (0.5). Por lo tanto, generará un error de caché y el procesador tendrá que acceder a la variable de una manera diferente, por ejemplo, a través de L2. Estaremos en este estado:
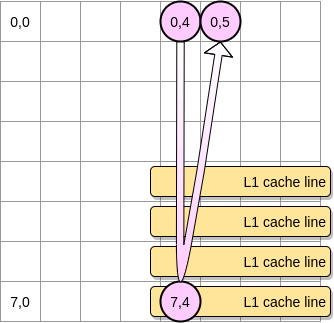
¿Qué tan pequeña debe ser una matriz para beneficiarse de L1? Vamos a contar un poco Primero, necesita saber el tamaño de la caché L1:
$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768
En mi máquina, el caché L1 es de 32,768 bytes mientras que la línea de caché L1 es de 64 bytes. De esta manera, puedo almacenar hasta 512 líneas de caché en L1. ¿Qué pasa si ejecutamos el mismo punto de referencia con una matriz de 512 elementos?
BenchmarkMatrixCombination-512 1404 718594 ns/op
BenchmarkMatrixReversedCombination-512 1363 850141 ns/opp
Aunque arreglamos la brecha (en una matriz de 64k la diferencia fue aproximadamente 4 veces), aún podemos notar una ligera diferencia. ¿Qué podría estar mal? En los puntos de referencia, trabajamos con dos matrices. Por lo tanto, el procesador debe mantener las líneas de caché de ambos. En un mundo ideal (no hay otras aplicaciones ejecutándose, etc.), el caché L1 está lleno al 50% con datos de la primera matriz y 50% de la segunda. ¿Qué pasa si redujimos el tamaño de la matriz a la mitad para trabajar con 256 elementos:
BenchmarkMatrixCombination-256 5712 176415 ns/op
BenchmarkMatrixReversedCombination-256 6470 164720 ns/op
Finalmente, hemos llegado al punto en que los dos resultados son (casi) equivalentes.
. ? , Go. - LEA (Load Effective Address). , . LEA .
, int64 , LEA , 8 . , . , . , () .
Ahora, ¿cómo limitar el impacto de los errores de caché en el caso de una matriz más grande? Hay un método, que se llama optimización de bucles anidados (optimización de anidación de bucles). Para aprovechar al máximo las líneas de caché, solo debemos iterar dentro de un bloque determinado.
Definamos un bloque en nuestro ejemplo como un cuadrado de 4 elementos. En la primera matriz, iteramos de (4.0) a (4.3). Luego pasa a la siguiente fila. En consecuencia, iteramos sobre la segunda matriz solo de (0.4) a (3.4) antes de pasar a la siguiente columna.
Cuando el puntero rosado pasa sobre la primera columna, el procesador almacena la línea de caché correspondiente. Por lo tanto, repasar el resto del bloque significa aprovechar L1:
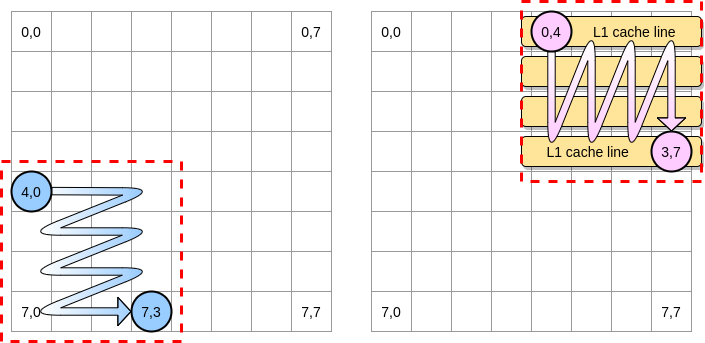
Escribamos una implementación de este algoritmo en Go, pero primero debemos elegir cuidadosamente el tamaño del bloque. En el ejemplo anterior, era igual a la línea de caché. No debe ser más pequeño, de lo contrario almacenaremos elementos que no serán accesibles.
En nuestro benchmark Go, almacenamos elementos int64 (8 bytes cada uno). La línea de caché es de 64 bytes, por lo que puede contener 8 elementos. Entonces el valor del tamaño del bloque debe ser al menos 8:
func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
blockSize := 8
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i += blockSize {
for j := 0; j < matrixLength; j += blockSize {
for ii := i; ii < i+blockSize; ii++ {
for jj := j; jj < j+blockSize; jj++ {
matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
}
}
}
}
}
}
Nuestra implementación ahora es un 67% más rápida que cuando iteramos en toda la fila / columna:
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000 6 185375690 ns/op
Este fue el primer ejemplo que demostró que comprender el funcionamiento de los cachés de la CPU puede ayudar a diseñar algoritmos más eficientes.
Intercambio falso
Ahora entendemos cómo el procesador gestiona los cachés internos. Como resumen rápido:
- El principio de localidad por distancia obliga al procesador a tomar no solo una dirección de memoria, sino una línea de caché.
- El caché L1 es local para un núcleo de procesador.
Ahora analicemos un ejemplo con coherencia de caché L1. La memoria principal almacena dos variables
var1y var2. Un hilo en un núcleo accede var1, mientras que otro hilo en el otro núcleo accede var2. Suponiendo que ambas variables son continuas (o casi continuas), terminamos en una situación en la que está var2presente en ambas memorias caché.
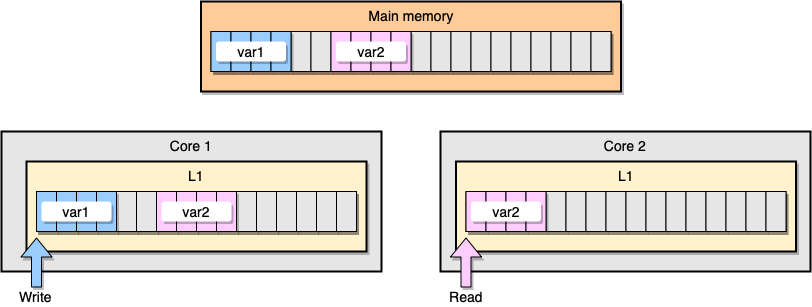
Ejemplo L1 Caché
¿Qué sucede si el primer hilo actualiza su línea de caché? Potencialmente puede actualizar cualquier ubicación de su cadena, incluyendo
var2. Luego, cuando se lee el segundo subproceso var2, el valor puede no ser coherente.
¿Cómo mantiene el procesador la caché coherente? Si dos líneas de caché tienen direcciones compartidas, el procesador las marca como compartidas. Si un hilo modifica una línea compartida, marca ambos como modificados. Se requiere coordinación entre núcleos para garantizar la coherencia de los cachés, lo que puede degradar significativamente el rendimiento de la aplicación. Este problema se llama intercambio falso .
Consideremos una aplicación Go específica. En este ejemplo, creamos dos estructuras una tras otra. Por lo tanto, estas estructuras deben ser secuenciales en la memoria. Luego creamos dos goroutines, cada uno de ellos se refiere a su propia estructura (M es una constante igual a un millón):
type SimpleStruct struct {
n int
}
func BenchmarkStructureFalseSharing(b *testing.B) {
structA := SimpleStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
En este ejemplo, la variable n de la segunda estructura solo está disponible para la segunda rutina. Sin embargo, dado que las estructuras son contiguas en la memoria, la variable estará presente en ambas líneas de caché (suponiendo que ambas gorutinas estén programadas en hilos en núcleos separados, lo cual no es necesariamente el caso). Aquí está el resultado de referencia:
BenchmarkStructureFalseSharing 514 2641990 ns/op
¿Cómo evitar el intercambio de información falsa? Una solución es la memoria completa (relleno de memoria). Nuestro objetivo es garantizar que haya suficiente espacio entre dos variables para que pertenezcan a diferentes líneas de caché.
Primero, creemos una alternativa a la estructura anterior al llenar la memoria después de declarar la variable:
type PaddedStruct struct {
n int
_ CacheLinePad
}
type CacheLinePad struct {
_ [CacheLinePadSize]byte
}
const CacheLinePadSize = 64
Luego instanciamos las dos estructuras y continuamos accediendo a esas dos variables en gorutinas separadas:
func BenchmarkStructurePadding(b *testing.B) {
structA := PaddedStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Desde una perspectiva de memoria, este ejemplo debería parecer que las dos variables son parte de diferentes líneas de caché:
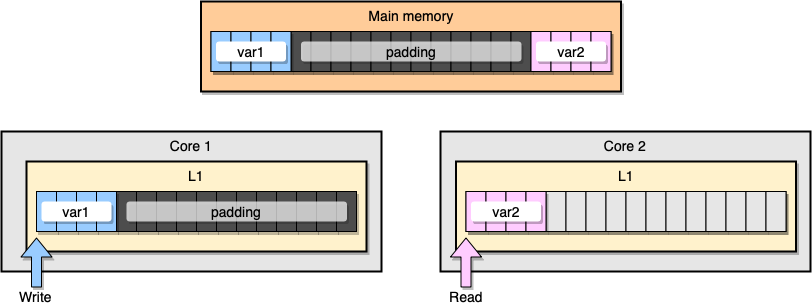
Relleno de memoria
Veamos los resultados:
BenchmarkStructureFalseSharing 514 2641990 ns/op
BenchmarkStructurePadding 735 1622886 ns/op
Un segundo ejemplo con el llenado de memoria es aproximadamente un 40% más rápido que nuestra implementación original. Pero también hay un inconveniente. El método acelera el código, pero requiere más memoria.
La mecánica de gusto es un concepto importante cuando se trata de optimizar aplicaciones. En este artículo, hemos visto ejemplos de cómo comprender la CPU nos ha ayudado a mejorar la velocidad del programa.
¿Qué más leer?