
Muchas gracias. Pido disculpas por sentarme aquí. Soy un hombre muy viejo
Mi tema de hoy es, en cierto sentido, muy especial, porque es muy antiguo. Las torceduras son una parte integral de la vida humana, siempre están ahí. Los antiguos escribieron sobre esto. Esto está en gran medida fuera de nuestro control. Y en cierto sentido, parecen ser un grado extremo de complicación, solo un completo desastre.
Hay muchos tipos de desorden. Entonces, por pura coincidencia, hace muchos años comencé a lidiar con esta forma de complicación y, para mi completa sorpresa, encontré signos y, debo decir, signos muy claros de orden en los problemas. Así que hoy me gustaría presentarles algunos ejemplos de lo que esto significa. Prefiero la palabra "roto" a "desigual" porque para alguien que estudió latín, como yo en mi juventud distante, la desigualdad es lo opuesto a la uniformidad. Pero este no es el caso.
La igualdad es lo opuesto a la fractura, porque el mundo en su mayor parte nos parece lleno de fracturas.
Déjame mostrarte un par de objetos. Algunos de ellos son creados artificialmente. Otros son muy reales, en cierto sentido. Esto es lo real.

Esta es la coliflor. ¿Por qué te estoy mostrando coliflor, una planta común y antigua? Porque, a pesar de su rutina y antigüedad, es complejo y simple. Es complejo y simple. Por ejemplo, no es difícil pesarlo. El peso importa si vamos a comerlo. Pero supongamos que vamos a medir su superficie. Esto se está poniendo interesante. Después de cortar una de las flores de coliflor con un cuchillo afilado, y mirando de cerca, vemos toda la coliflor, solo que de un tamaño más pequeño. Luego puedes cortar una y otra y otra y otra y otra vez ... Y obtienes especímenes cada vez más pequeños de coliflor. La experiencia humana ha demostrado que hay formas con una propiedad tan interesante que cada parte es similar a la totalidad, pero de menor tamaño. ¿Y qué aprendió la persona de este hecho? Muy poco.
En relación con el estudio de este problema, descubrí algo completamente sorprendente: la deformación puede medirse mediante un número, digamos, 2.3 o 1.2, y a veces mucho más. Un día, un amigo mío trajo una fotografía y, medio en broma, preguntó: "¿Cuál es el doblez de esta curva?" Le dije: "Un poco menos de un año y medio". Resultó que era igual a 1,48. No me llevó mucho tiempo estudiar estas cosas por tanto tiempo. Los números en cuestión indican el grado de fractura de la superficie.

Permítanme hacer una reserva de inmediato que las superficies son absolutamente artificiales y fueron creadas en una computadora. El único punto de partida fue el número. Este número es retorcido. La fractura de la izquierda es el resultado de la copia de varios paisajes. A la derecha, yo mismo me doy una vuelta más alta. Si observa de cerca, después de un tiempo puede reconocer las diferencias en estos dos casos a simple vista.
El hombre tuvo que acostumbrarse al concepto de fractura. Esto está muy roto, pero esto, uno podría decir, es suave, pero esto es completamente suave. Pocas cosas son muy suaves. Hagámonos ahora la pregunta: ¿cuál es la superficie de la coliflor? Puede medirse, medirse y medirse ... Cuanto más precisa sea la medición, mayor será la superficie, etc., a distancias muy pequeñas. ¿Cuál es la longitud de la costa de estos lagos? Cuanto más precisa sea la medición, más tiempo resultará. El concepto de longitud de la costa, que parece tan obvio porque a menudo se cita, de hecho es completamente erróneo: simplemente no existe tal cosa. Debe haber un enfoque diferente.
¿Y de qué sirve este conocimiento? Sorprendentemente, hay muchos beneficios. Para empezar, los paisajes artificiales que yo, digamos, he inventado se usan constantemente en la cinematografía. Vemos montañas en la distancia. Puede ser montañas, pero puede ser simplemente fórmulas fluidas. Esto es muy fácil de lograr. Solía llevar mucho tiempo, pero ahora es un mero truco. Echa un vistazo aquí. Esto es luz real.
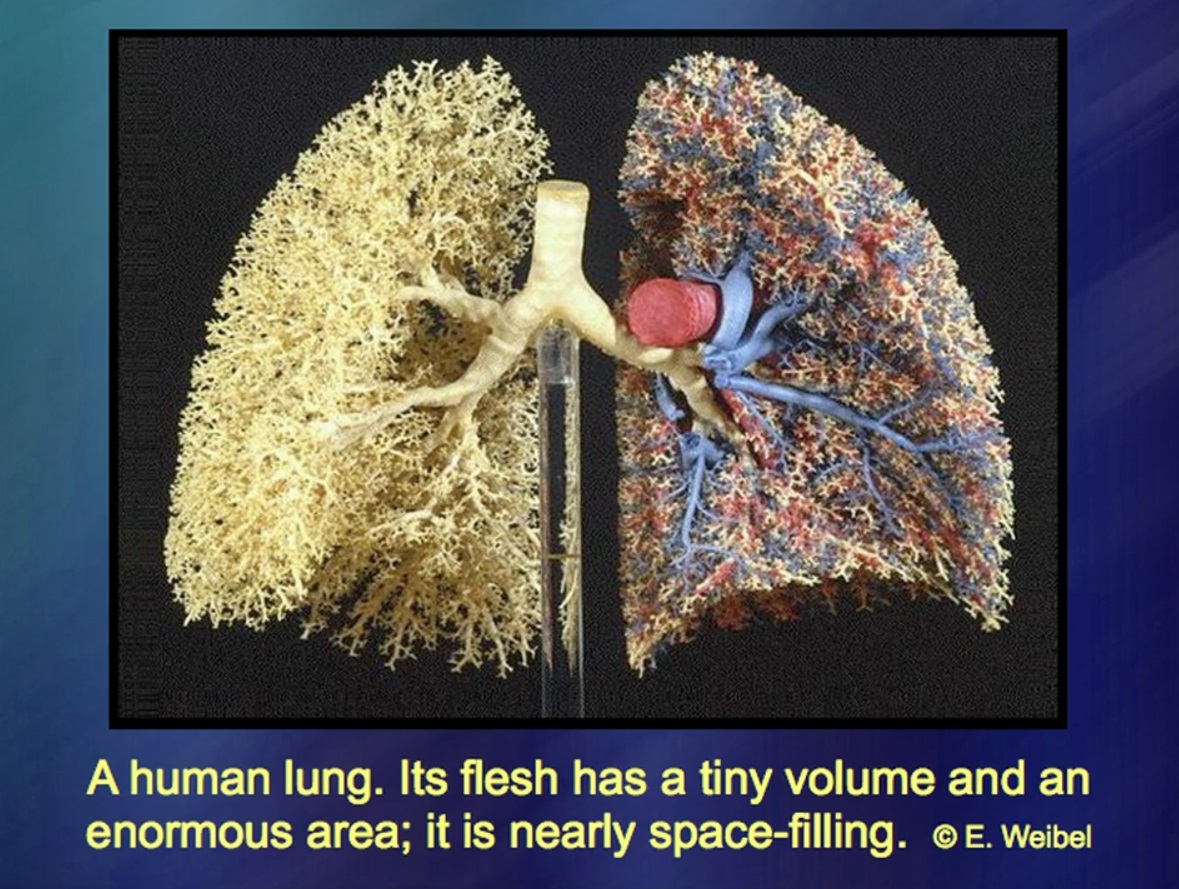
El pulmón es un objeto muy extraño. Todos sabemos muy bien que tiene algo de peso. También se sabe que el volumen del pulmón es muy pequeño. ¿Qué pasa con el área pulmonar? Los anatomistas han debatido durante mucho tiempo este tema. Se cree que en un hombre normal, el área del pulmón es igual al área de una pelota de baloncesto. Otros argumentan que no hay cinco bolas de este tipo. Las discrepancias son colosales. ¿Por qué? Porque el área del pulmón es un concepto muy vagamente definido. Los bronquios se ramifican y se ramifican más y más. Y dejan de ramificarse no por algún principio, sino por condiciones puramente físicas, por moco dentro del pulmón. Así es como se forma un pulmón mucho más grande: los bronquios se ramifican más y más profundo, mientras que la brecha entre ellos es aproximadamente la misma para una ballena, para una persona y para un pequeño roedor.
Entonces, ¿de qué sirve esto? Sorprendentemente e incluso asombrosamente, los anatomistas tenían una idea pobre de la estructura del pulmón hasta hace poco. Creo que mi investigación matemática, sorprendentemente, fue de gran ayuda para los cirujanos que estudian enfermedades pulmonares, así como enfermedades hepáticas, donde existen tales sistemas de ramas con una falta de geometría inteligible. En otras palabras, tuve que crear geometría para algo que no tiene su propia geometría. Se encontró una calidad sorprendente: muy a menudo las reglas de esta geometría son extremadamente concisas. Comienza con fórmulas cortas, aplíquelas varias veces, a veces repetidamente, una y otra vez. La misma repetición. Y al final resulta algo así.
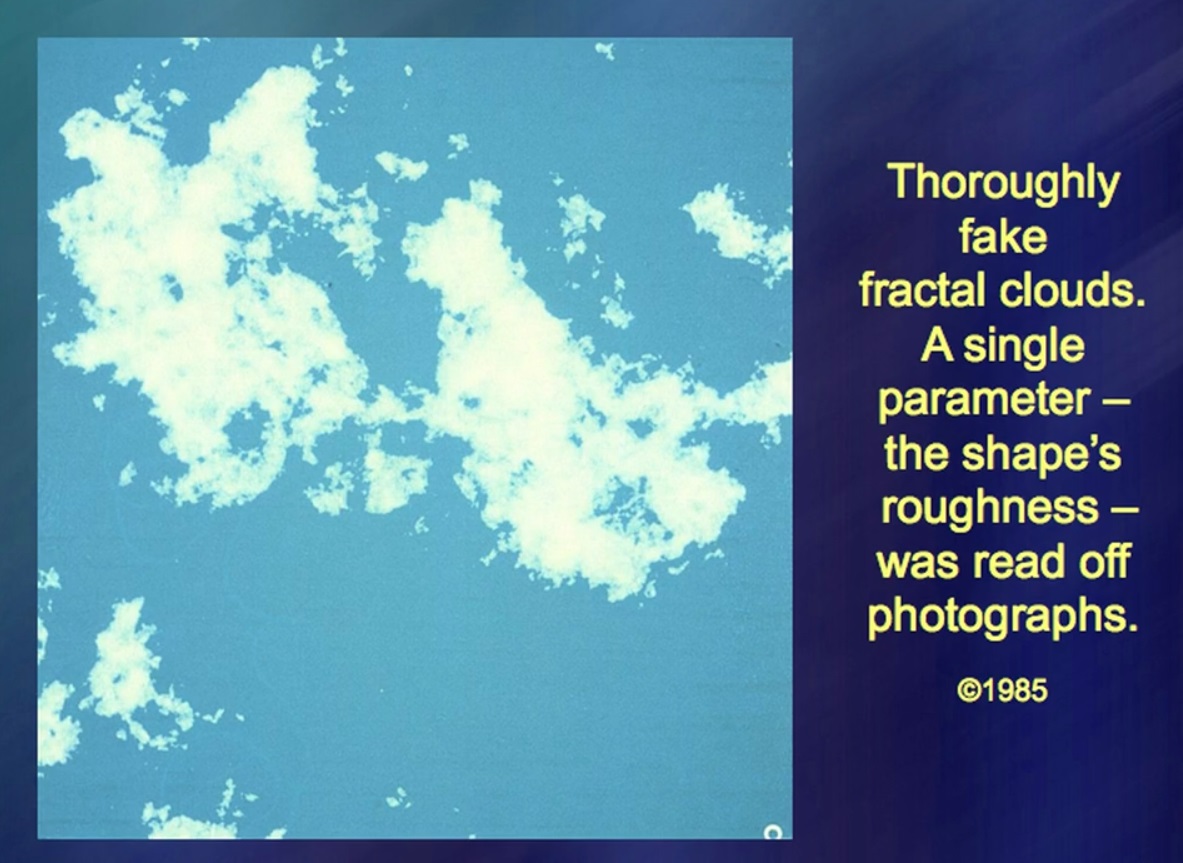
Esta nube es completamente artificial, 100%. De acuerdo, 99.9%. El único elemento natural aquí es el número, la fractura de la nube: este número está tomado de la naturaleza. Una cosa tan compleja como una nube, tan inestable, cambiante, obedece a una regla simple. Esta simple regla no es una explicación para la nubosidad. Pero el mar de nubes debe tener en cuenta esta regla. No sé cuán perfectas son estas viejas fotos. Hice esto intensamente, pero luego mi atención se dirigió a otros fenómenos.
Y aquí hay una cosa más interesante. Uno de los eventos revolucionarios en la historia de las matemáticas, insuficientemente apreciado por muchos, tuvo lugar hace unos 130 años, hace 145 años. Los matemáticos comenzaron a crear formas inexistentes. Entre los matemáticos, la capacidad de una persona para crear algo que nunca existió en la naturaleza ha llegado a ser apreciada, y en un grado absolutamente inimaginable. En particular, pudieron inventar una curva que llena todo el plano hasta el último punto. Una curva es una curva, un plano es un plano, y los dos no encajan entre sí. Resultó que encajan juntos.
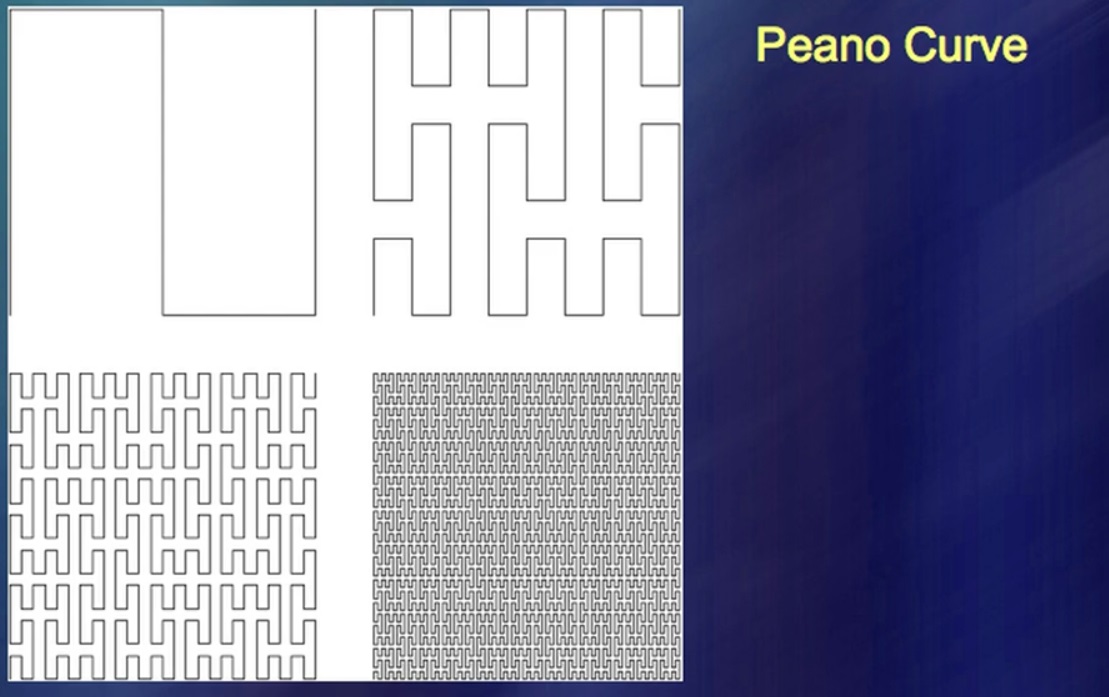
Un hombre llamado Peano identificó tales curvas y generaron un interés excepcional. Son muy importantes y despiertan interés en gran parte porque ha habido algún tipo de división de las matemáticas en una que se basa en la realidad y una que proviene de la razón pura. Desafortunadamente, probé que lo que se supo a través de los esfuerzos de la razón pura, de hecho, se conoce desde hace mucho tiempo en una forma diferente. Aquí tengo un sistema de riachuelos en forma de curvas que llenan el plano.

En sí mismo, esto es historia. Fue entre 1875 y 1925, un momento increíble cuando las matemáticas se preparaban para separarse del mundo real. Ciertos objetos han servido como una ilustración de la brecha, desde mi infancia y mis años de estudiante, la brecha entre las matemáticas y la realidad visible. Sin embargo, logré repensarlos, ponerlos al revés y, con su ayuda, describir algunos aspectos de la complejidad de la naturaleza.
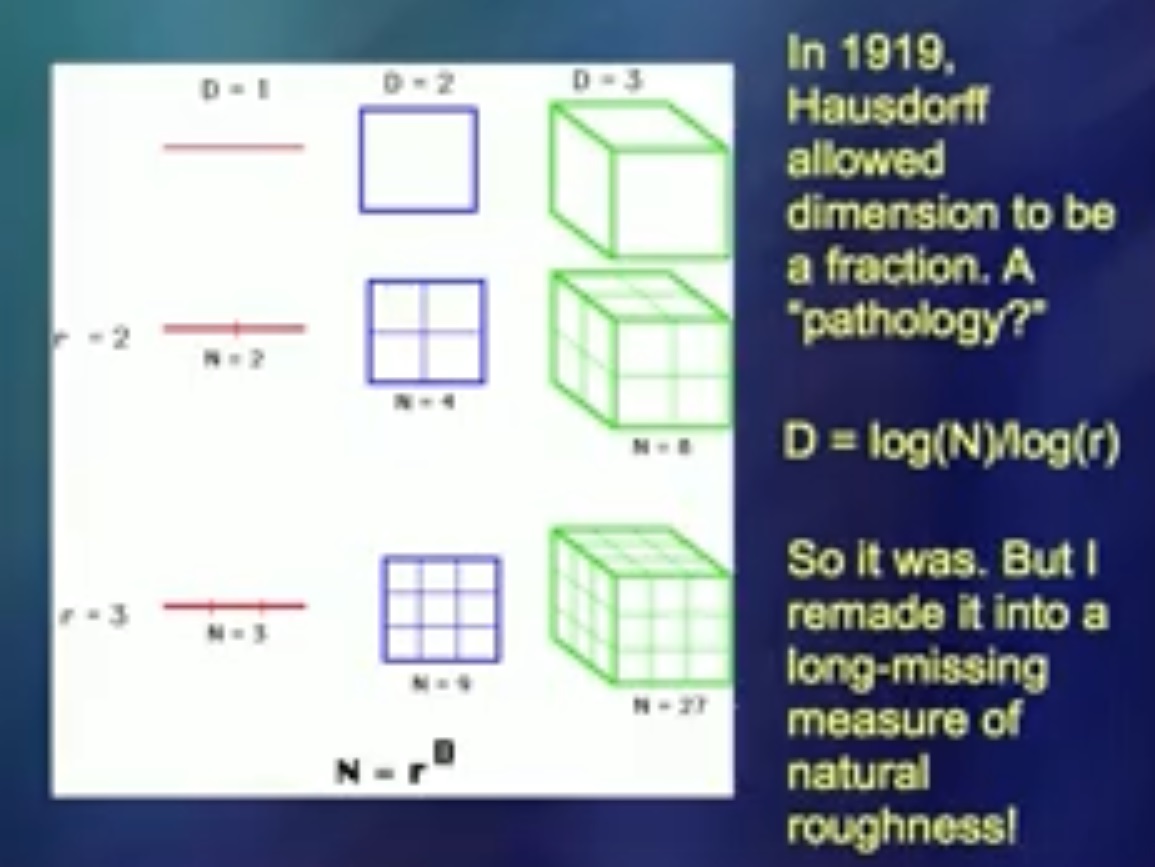
En 1919, un hombre llamado Hausdorff identificó un número que podría considerarse una broma matemática. Pero he descubierto que este número es una buena herramienta para medir el pliegue. Cuando les dije esto a mis colegas por primera vez, me dijeron: "No seas tonto. Esto es algo ... ”En realidad, no estaba haciendo cosas estúpidas.

El gran artista Hokusai lo sabía muy bien. En la parte inferior de la imagen hay algas. Hokusai no sabía las matemáticas necesarias: simplemente no existía entonces. Además, siendo japonés, él [en ese momento] no tenía contacto con Occidente. Pero el arte ha contenido elementos fractales durante mucho tiempo. Puedo hablar sobre esto por mucho tiempo.

La Torre Eiffel tiene elementos fractales. Leí el libro de Eiffel sobre su torre; el alcance de su comprensión es sorprendente.
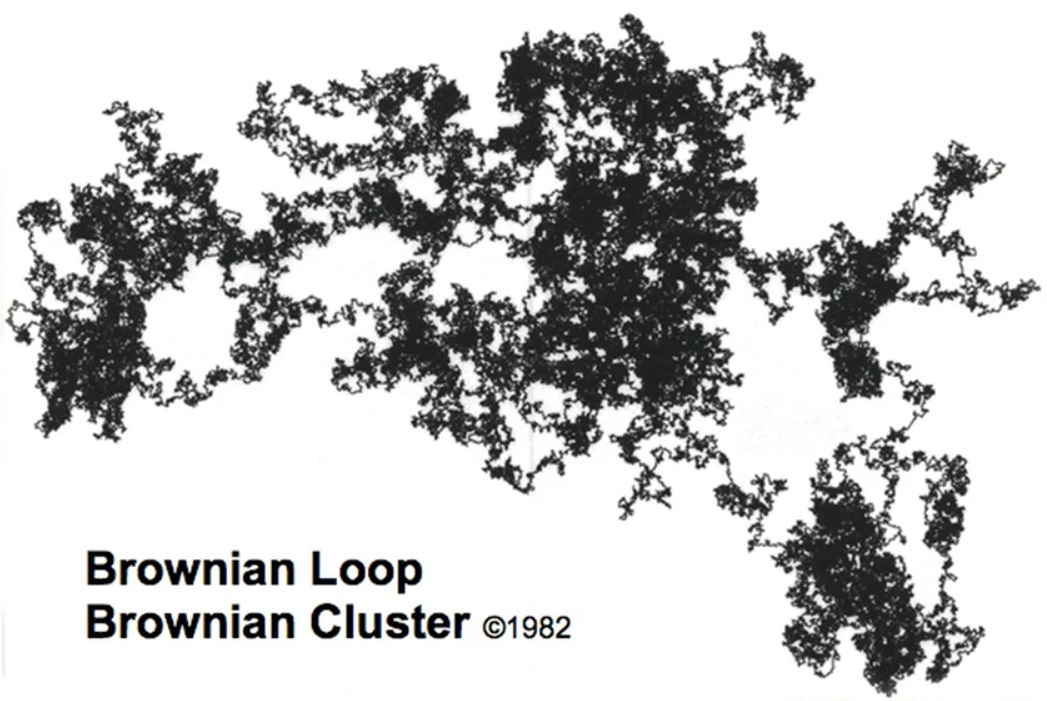
Aquí hay un desastre dentro de un desastre. Bucle browniano. Una vez que decidí que había pasado por una parte considerable de mi vida profesional, y que me ocupaban tantas cosas diferentes, decidí que era hora de ponerme a prueba. ¿Puedo explorar un objeto que todos han estado explorando durante mucho tiempo y encontrar algo radicalmente nuevo en él? Comencé a estudiar todo lo que cae en la categoría de movimiento browniano. Probé diferentes ángulos, probé diferentes métodos y regresé a donde comencé. Luego le sugerí a mi asistente: “No veo nada aquí. ¿Puedes pintar? " Lo hizo, es decir, llenó todo el interior. "Me las arreglé ..."

Pero grité: "¡Alto! ¡Detener! ¡Detener! Entendido: esta es una isla ". Asombroso. El movimiento browniano tiene un doblez igual a dos. Lo mido, resulta 1.33. Mido una y otra vez. Mediciones largas, grandes movimientos brownianos. De nuevo: 1.33. Un problema matemático surge de inmediato: ¿cómo probarlo? Le tomó a mis amigos 20 años. Tres tenían evidencia incompleta. Unieron fuerzas y juntos lograron obtener pruebas. Como resultado, recibieron la famosa medalla [Fields] para matemáticos. En general, los matemáticos recibieron tres medallas [Fields] por probar hechos que vi pero que no pude probar.
Ahora la gente me pregunta en todas partes: “¿Cómo empezó todo? ¿Cómo te condujeron tus estudios a cosas tan inusuales?
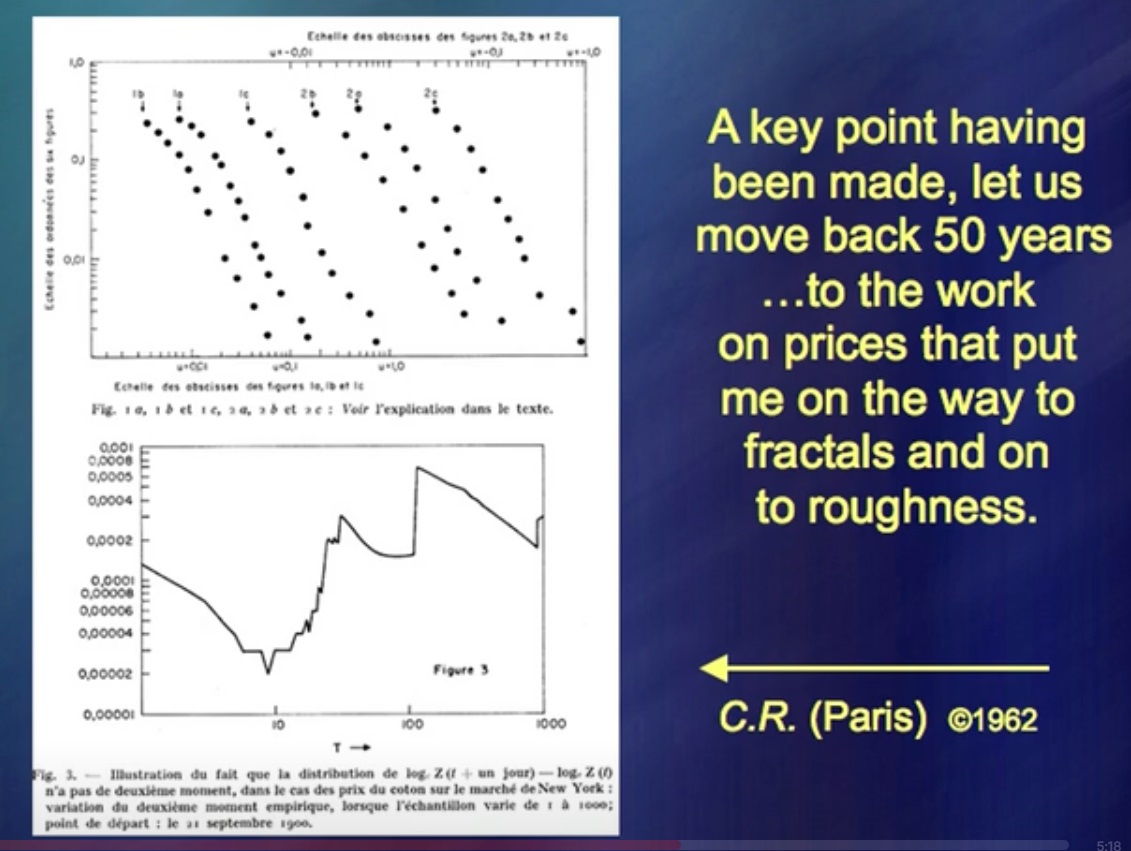
¿Qué me permitió ser simultáneamente ingeniero mecánico, geógrafo, matemático, etc.? Por extraño que parezca, pero comencé estudiando los precios en el mercado de valores.

Tenía una teoría y escribí libros al respecto.
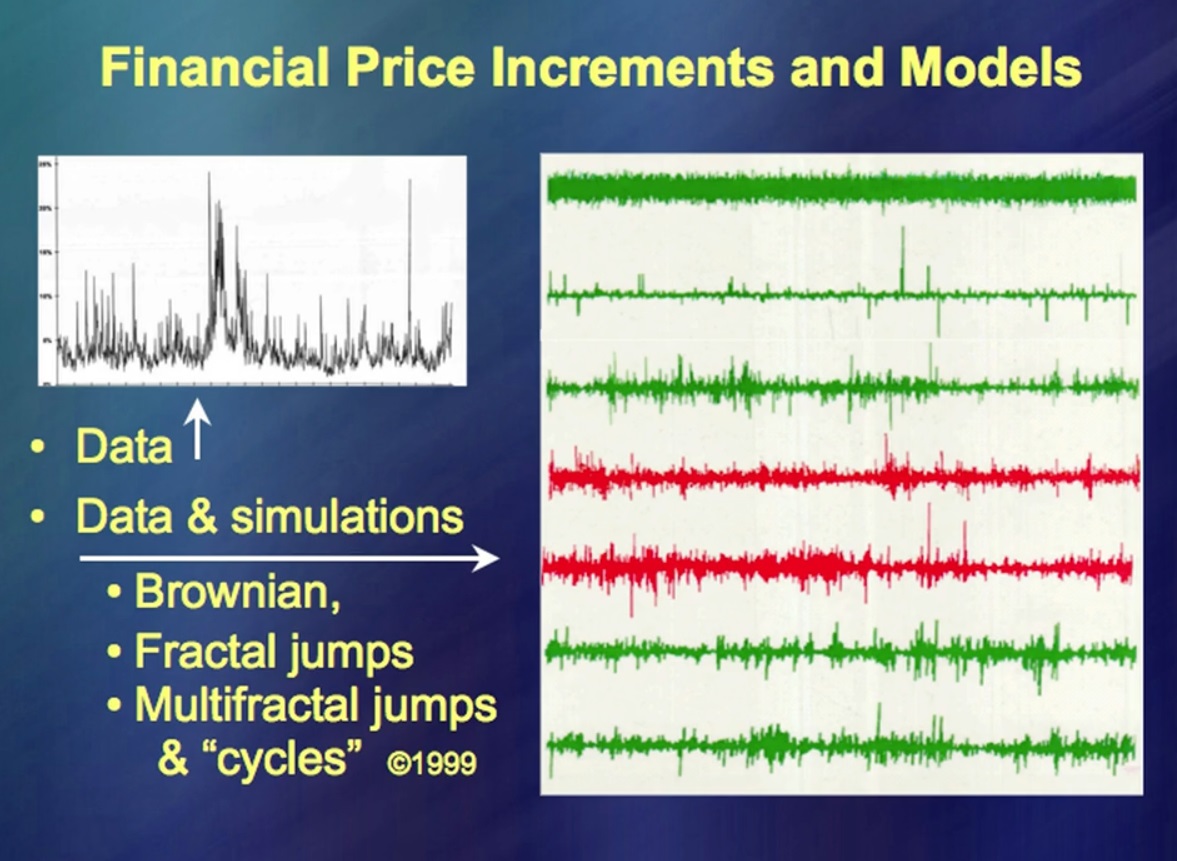
"Movimientos de precios de los instrumentos financieros" A la izquierda puede ver los datos durante un largo período, a la derecha, en la parte superior, los datos de acuerdo con una teoría muy, muy de moda. Es extremadamente simple y puedes escribir muchos libros al respecto muy rápidamente. (Risas) Hay miles de libros sobre este tema. Ahora compare con los movimientos de precios reales. Y donde estan Las líneas adicionales incluyen movimientos de precios reales, así como una pequeña falsificación de mi parte. La idea principal era que necesita poder hacer ... ¿Cómo se llama? ... Simulación de fluctuaciones de precios. Esto funcionó muy bien hace 50 años.
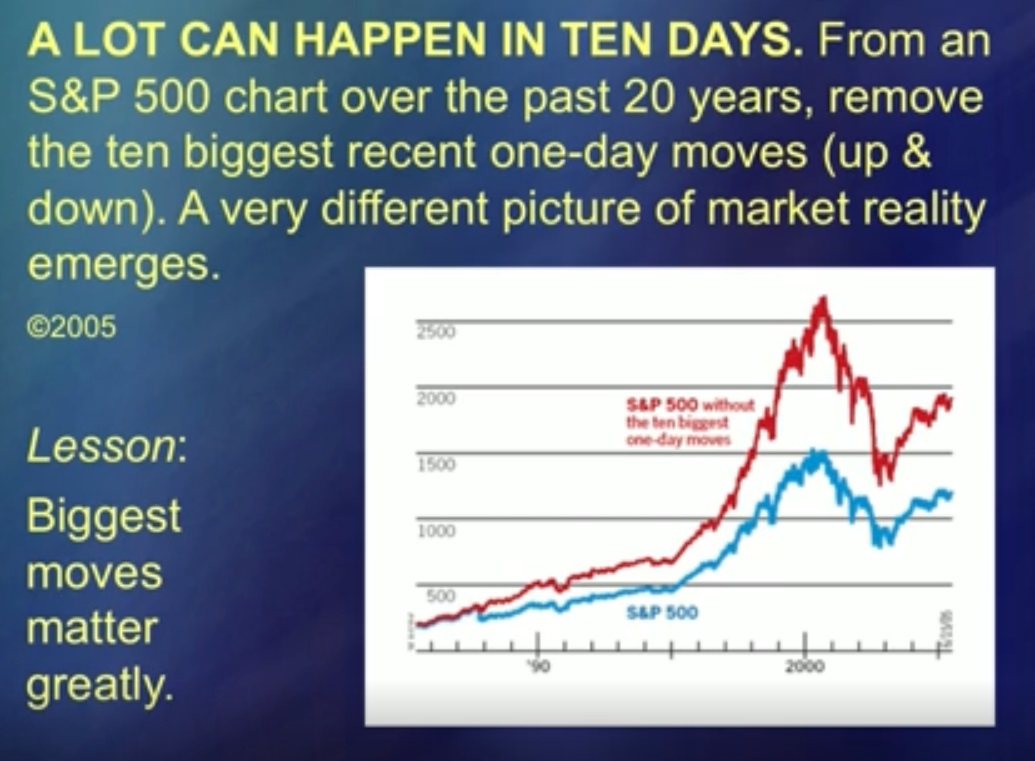
Durante 50 años, mi idea fue ridiculizada porque podría haberse hecho más fácilmente. Pero ahora, te digo, comenzaron a escucharme. (Risas) Estas dos curvas representan promedios. El azul es el Standard and Poor's [S&P 500] y el rojo es el Standard and Poor's, del cual se han restado los 5 picos de precios más grandes. El salto ciertamente arruina el análisis, y en muchos estudios se considera [no analítico] un caso especial. “Increíble coincidencia, intervención del Señor. Bueno, una pequeña cosa, puedes dejarlo a un lado ". Las intervenciones del Señor en este gráfico, y hay exactamente cinco de ellas, como resultado, son tan importantes como todo lo demás. En otras palabras, las intervenciones del Señor no se pueden dejar de lado.
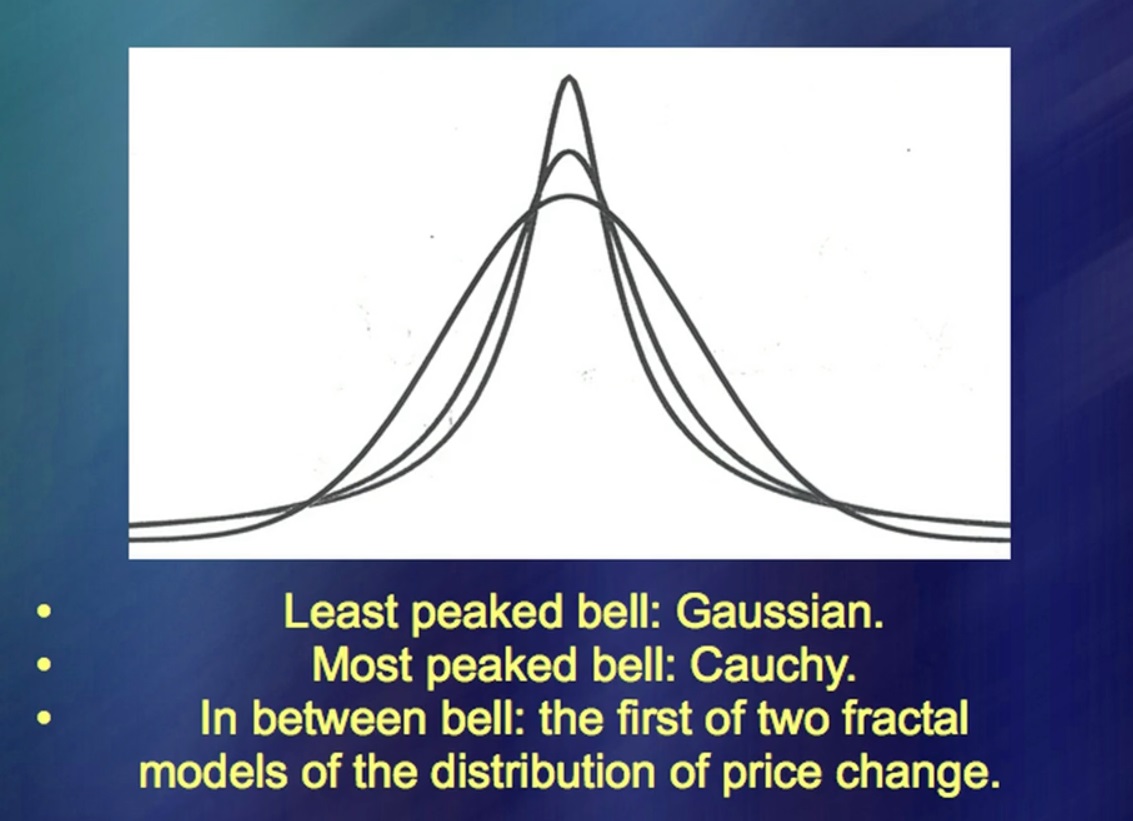
Es un ser, es el mismo objeto de análisis. Si trata con ellos, también puede lidiar con los movimientos de precios. Pero no he descubierto los saltos, entonces puedes analizar el llamado ruido tanto como quieras, pero este análisis no tendrá sentido. Estas curvas muestran el impacto.

Ahora pasaré al último tema: el conjunto que lleva mi nombre. En cierto modo, esta es la historia de mi vida. Mi adolescencia la pasé en Francia, que fue ocupada por Alemania en esos años. Como pensaba que en cualquier momento podría no serlo, tuve grandes sueños. Después de la guerra, me encontré con mi tío otra vez. Mi tío era un matemático sobresaliente y dijo: “Aquí hay un problema para ti. Hace 25 años no pude resolverlo, y nadie puede resolverlo. Esta es la construcción de un matemático llamado Gaston Julia y otro llamado Pierre Fatou. Si puede encontrar algo nuevo aquí, cualquier cosa, considere que su carrera está asegurada ". Muy simple. Comencé a estudiar este problema y, como miles de los que intentaron hacerlo antes que yo, no lograron nada.
Pero luego aparecieron las computadoras. Y decidí que necesitaba aplicar la potencia informática no a nuevos problemas matemáticos, como, por ejemplo, esta curva: es un problema nuevo, sino a problemas antiguos. Y cambié de los llamados números reales, es decir desde puntos en línea recta hasta números complejos, y estos son puntos en un plano, es decir, lo que se requiere en este problema. El resultado es una figura así.

Este es de una complejidad excepcional. La ecuación está oculta en ella: z se transforma en z ^ 2 + c. Tan simple y aburrido, tan poco interesante. Ahora vamos a ejecutarlo una, dos veces ... Dos veces es suficiente. Sobre un milagro! Esto es lo que aparece. No voy a explicar estas cosas aquí, pero resulta que esto es qué y esto es qué.


Figuras de tal complejidad, tal armonía y tanta belleza se obtienen repetidamente, una y otra y otra vez. Mi descubrimiento principal fue que estas islas tienen la misma forma, más o menos, que toda la figura. El resultado es una impresionante joyería barroca.

Y toda esta breve fórmula, en la que hay de todo, ¿cuánto hay? - cinco iconos Y este es el resultado.

El color se agregó por dos razones. En primer lugar, porque las cifras son tan complejas que es difícil ver qué significado tienen los números. Y debe elegir algún tipo de sistema para reflejarlos en el avión. Por lo tanto, tomé como principio representar siempre las figuras en diferentes colores: un color significa una cosa y otro significa otra, etc. Es muy dificil.
En 1990, estaba en el Reino Unido, en Cambridge, donde recibí un premio de la universidad. Tres días después, un piloto, volando sobre el campo, vio esto.

¿De dónde vendría tal cosa? Por supuesto, de los extraterrestres.
Uno de los periódicos de Cambridge publicó un artículo sobre este "descubrimiento", y al día siguiente recibió 5.000 cartas, que decían que este es el conjunto de Mandelbrot, simplemente muy grande.

Déjame terminar. Esta imagen se obtiene a través de las matemáticas puras. Las reglas simples pueden crear un milagro sin fondo si se repiten sin cesar.
Traducido por Namik Kasumov
Revisado por Ekaterina Tsvetkova

Descubra los detalles de cómo obtener una profesión de alto perfil desde cero o subir de nivel en habilidades y salario tomando los cursos en línea pagos de SkillFactory:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )