Clasificación inferior del montón

Este es el artículo final de la serie de clasificación de montón. En conferencias anteriores, observamos una amplia variedad de estructuras de montón que muestran excelentes resultados de velocidad. Esto plantea la pregunta: ¿qué montón es el más eficiente a la hora de ordenar? La respuesta es: la que veremos hoy.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

Los montones elegantes que vimos anteriormente están bien, pero el montón más eficiente es el montón estándar con limpieza mejorada.



Qué es el cribado, por qué se necesita en el montón y cómo funciona, descrito en la primera parte de una serie de artículos.



El cribado estándar en la clasificación clásica por grupo funciona aproximadamente como "frente": un elemento de la raíz del subárbol se envía al portapapeles, los elementos de la rama, según los resultados de la comparación, suben. Es bastante simple, pero hay demasiadas comparaciones.







En la pantalla ascendente, las comparaciones se guardan debido al hecho de que los padres casi no se comparan con los descendientes, básicamente, solo los descendientes se comparan entre sí. En un montón común, tanto el padre se compara con los niños como los niños se comparan entre sí, por lo tanto, hay casi una vez y media más comparaciones con el mismo número de intercambios.



Entonces, cómo funciona, echemos un vistazo a un ejemplo específico. Digamos que tenemos una matriz en la que casi se forma un montón: todo lo que queda es tamizar a través de la raíz. Para todos los demás nodos, la condición se cumple: cualquier hijo no es más grande que su padre.



En primer lugar, desde el nodo para el que se realiza el borrado, debe descender a lo largo de los descendientes grandes. El montón es binario, es decir, tenemos un hijo izquierdo y un hijo derecho. Bajamos a esa rama donde el descendiente es más grande. En esta etapa, se realiza el número principal de comparaciones: los descendientes izquierdo / derecho se comparan entre sí.







Al llegar a la hoja en el último nivel, decidimos sobre la rama, los valores en los que deben cambiarse. Pero no necesita mover toda la rama, sino solo la parte que es más grande que la raíz desde la que comenzó.



Por lo tanto, subimos la rama al nodo más cercano, que es más grande que la raíz.







El último paso es utilizar una variable de búfer para mover los valores del nodo hacia arriba de la rama.







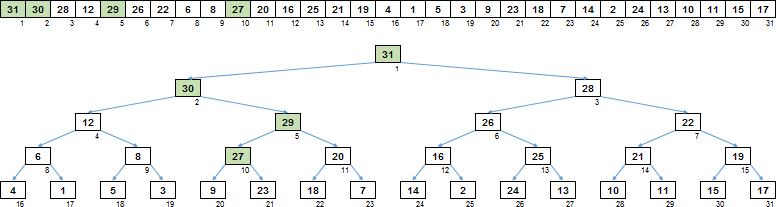
Eso es. Un claro ascendente ha formado un árbol de clasificación a partir de una matriz, en la que cualquier padre es mayor que sus descendientes.



Animación final:

Implementación de Python 3.7

El algoritmo de clasificación básico no es diferente del montón habitual:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

El descenso a la hoja inferior se puede extraer convenientemente / visualmente en una función separada:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

Y lo más importante: un claro, primero bajando, luego emergiendo hacia arriba:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

Puramente empíricamente: de acuerdo con mis mediciones, la ordenación del montón ascendente es 1.5 veces más rápida que la ordenación del montón normal.



De acuerdo con cierta información (en la página del algoritmo en Wikipedia, en los archivos PDF proporcionados en la sección "Enlaces"), BottomUp HeapSort está en promedio antes de una clasificación rápida, incluso para conjuntos bastante grandes de 16 mil elementos o más.

Enlaces

Clasificación ascendente ascendente



Una variante de clasificación ordenada con un número casi óptimo de comparaciones



Construcción rápida de montones



Una nueva variante de clasificación de latidos, en promedio, clasificación rápida (si n no es muy pequeño)

Artículos de la serie:

• Aplicación Excel AlgoLab.xlsm
• Ordenar intercambios
• Ordenar inserciones
• Selección de selección
  • Tipos de montón: pirámides n-ary
  • Clases de montón: números de Leonardo
  • Clases de montón: montón débil
  • Tipo de montón: árbol cartesiano
  • Clases de montón: árbol de torneo
  • Clasificación de montón: limpieza ascendente
• Combinar clasificaciones
• Ordenar por distribución
• Clases híbridas

La clasificación de hoy se ha agregado a la aplicación AlgoLab, que la está utilizando: actualice el archivo de Excel con macros.