
Nacido para gatear no puede volar. Esta frase puede usarse tanto en sentido metafórico como en sentido literal, porque las criaturas sin alas (o partes del cuerpo funcionalmente similares) realmente no pueden conquistar los cielos. Al menos la mayoría de ellos. La regla no sería la regla si no hubiera excepciones. En el aspecto del vuelo no volador, también hay excepciones: serpientes de árbol decoradas ( Chrysopelea) Los representantes de este género de serpientes son capaces de volar, una habilidad extremadamente útil dado que viven en las copas de los árboles muy por encima del suelo. Científicos de la Universidad Politécnica de Virginia (EE. UU.) Decidieron considerar el vuelo de una cometa desde el punto de vista de la cinemática. ¿Qué características anatómicas permiten que las serpientes vuelen (caen de forma controlada, para ser exactos), qué sucede durante el vuelo en términos de cinemática y cómo puede ayudar esta investigación en robótica? Las respuestas a estas preguntas nos esperan en el informe de los científicos. Vamos.
Base de estudio
Las serpientes de árbol decoradas son un género de serpientes de la familia de la misma, que viven en el sur y sureste de Asia. Los representantes de este género no pueden presumir de grandes dimensiones (longitud del cuerpo solo de 0.6 a 1.5 m) y veneno mortal. Aunque la presa que cazan durante el día no estaría de acuerdo con la última. Dado el hábitat (coronas de los árboles), estas serpientes tienen muy pocos enemigos, por lo tanto, no tienen una necesidad especial de veneno fuerte. Además, tienen tácticas mucho más efectivas: saben cómo planificar.

Las serpientes voladoras, como se las llama popularmente, se arrastran a través de los árboles usando escamas duras a lo largo de su vientre, lo que les permite moverse verticalmente. Si la serpiente quiere moverse de un árbol a otro, primero se arrastra hacia el borde de la rama, luego dobla el cuerpo en la forma de la letra latina "J" para apuntar (para determinar el ángulo deseado de "despegue" y el lugar de aterrizaje). Al decir "vámonos", la serpiente empuja su cuerpo hacia adelante y hacia arriba, estirando su estómago y sobresaliendo sus costillas (por lo que su cuerpo se vuelve más plano y ligeramente cóncavo). Durante la planificación, la serpiente realiza constantemente movimientos serpentinos del cuerpo de un lado a otro, lo que le permite controlar el vuelo y aterrizar suavemente.
Vista lateral de una serpiente voladora de deslizamiento largo Chrysopelea paradisi.
Una ventaja adicional del método de movimiento tan inusual para las serpientes es el impresionante ahorro de energía, porque el vuelo es mucho más rápido (y más seguro) que gatear lentamente de un árbol a otro en el suelo. A partir de esta breve descripción, queda claro que hay muchos elementos importantes en la mecánica del vuelo de la serpiente; ángulo de despegue, forma del cuerpo durante el despegue y el vuelo, movimiento del cuerpo en vuelo, etc.
El aspecto más llamativo, especialmente para los observadores, del vuelo de la serpiente es el movimiento ondulado del cuerpo. Esta técnica es utilizada por muchas criaturas en el planeta para moverse por tierra y agua. No es necesario ir lejos, ya que las serpientes lo usan perfectamente. Los científicos señalan que el movimiento ondulado en tierra y agua se ha estudiado bastante bien, pero tales piruetas en el aire siguen siendo un misterio.
En las serpientes Chrysopelea , la ondulación se caracteriza por una forma de cuerpo en forma de S, una baja frecuencia de ondulación (1–2 Hz) y una sección transversal aerodinámica aplanada del cuerpo.
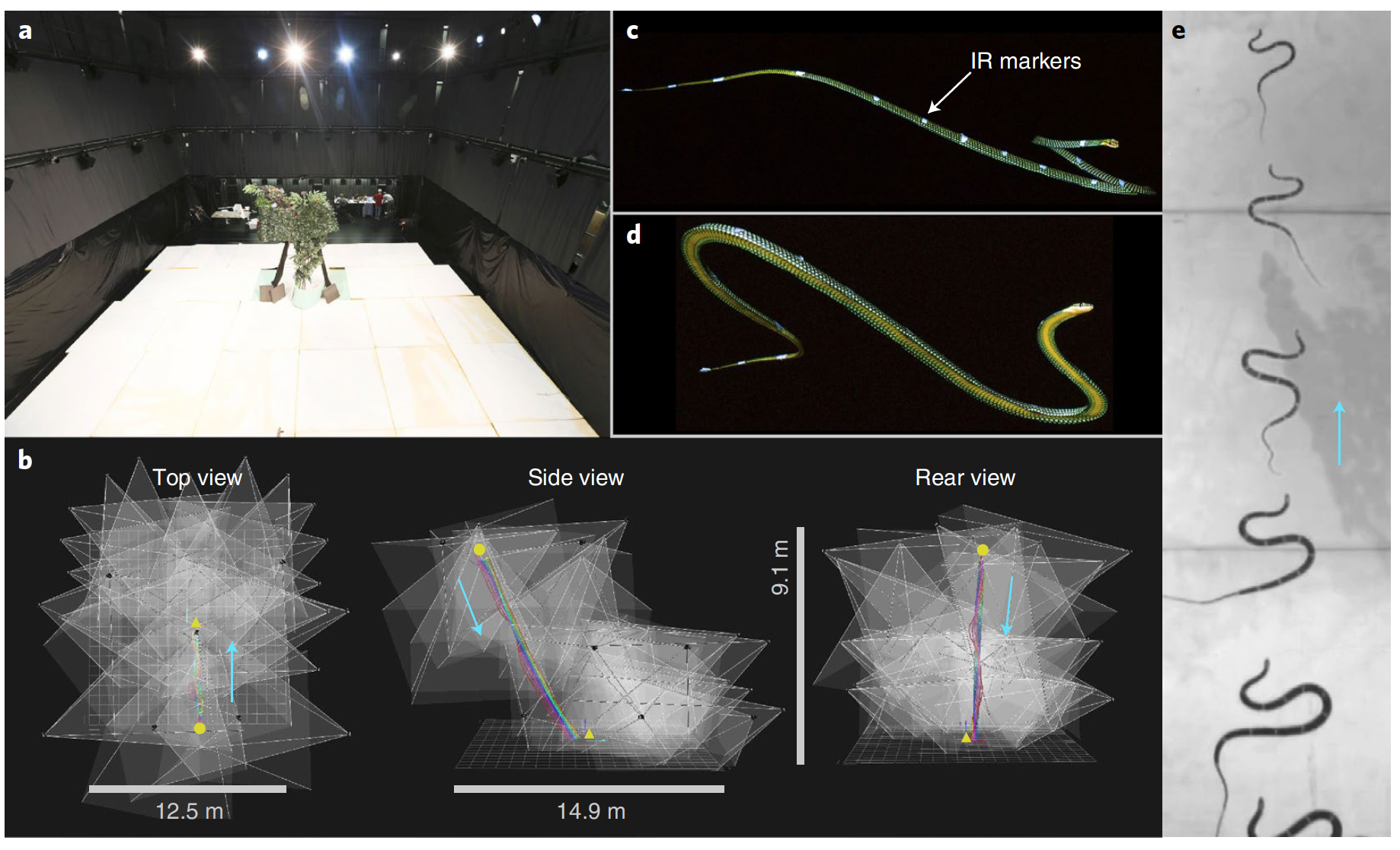
Imagen No. 1
De hecho, la ondulación ondulada reconstruye continuamente el cuerpo de la serpiente, transformándola en forma en un ala ( 1e) Investigaciones anteriores han demostrado que las cometas voladoras siempre realizan movimientos ondulados en vuelo. Sin embargo, no está claro si la ondulación es una parte esencial de un vuelo exitoso o si es solo un hábito. El aspecto conductual de moverse en tierra, migró a la fuga sin ninguna intención.
Si tenemos en cuenta la ondulación en tierra y agua, entonces podemos suponer que en el aire genera empuje. En medios sólidos, el movimiento ondulante se produce debido a las fuerzas de contacto distribuidas sobre las regiones ventral y lateral del cuerpo, y en el agua, el desplazamiento o la absorción de líquido a lo largo del cuerpo provoca un movimiento hacia adelante. En ambos casos, la fuerza impulsora pura actúa principalmente en el plano de ondulación. La modulación del cuerpo fuera del plano (vertical) se puede utilizar para fines secundarios, como disminuir la resistencia o aumentar la fuerza normal.
Pero para volar cometas, una planificación exitosa requiere la generación de fuerzas aerodinámicas necesarias para compensar el peso del animal. Las fuerzas de elevación y resistencia son creadas por el aire que fluye a través del cuerpo aplanado cuando es acelerado hacia abajo por la gravedad, y el movimiento recíproco causado por las contracciones musculares probablemente no aumenta la generación de fuerza.
Vista frontal del despegue y aplanamiento de la serpiente voladora Chrysopelea paradisi.
Las fuerzas aerodinámicas resultantes deben actuar fuera del plano de ondulación, y la ondulación misma debe cambiar constantemente la distribución de fuerzas en el cuerpo de la serpiente. También vale la pena considerar que las cometas voladoras pueden "revolotear" no solo horizontalmente, sino verticalmente. Esto significa que el modelo de vuelo de la cometa contiene elementos de pitch * y roll * .
Paso * : movimiento angular relativo al eje transversal horizontal de inercia.En este estudio, los científicos decidieron examinar en detalle el papel de la ondulación en el vuelo de la serpiente. Utilizando grabaciones de vuelo de serpiente a alta velocidad, los científicos pudieron cuantificar la ondulación en el aire. Los datos obtenidos nos permitieron crear un modelo tridimensional preciso del vuelo de la serpiente.
Roll * - movimiento angular sobre su eje longitudinal.
Resultados de la investigacion
La ondulación aérea consiste en un montón de ondas de flexión horizontal y vertical. Se colocaron entre 11 y 17 marcadores a lo largo del cuerpo de las serpientes (7 individuos) que participaron en el tiroteo del vuelo (área de despegue alta de 8.3 m). Evaluar el cambio de posición de estos marcadores le permite determinar con precisión la estructura de la ondulación durante el vuelo.
Vista superior del deslizamiento de prueba de una serpiente voladora Chrysopelea paradisi.
Marcadores infrarrojos obtenidos mientras se deslizaba una serpiente voladora, Chrysopelea paradisi.
Después de 36 observaciones prácticas, los científicos crearon un modelo tridimensional del cuerpo de la serpiente ( r ).
Desarrollo de un modelo 3D de la cometa voladora Chrysopelea paradisi según datos de captura de movimiento.
Usando el vector tangente (t̂ = ∂r / ∂s), fue posible descomponer la ondulación en dos ondas de flexión angular que se mueven a lo largo del cuerpo.
Las ondas horizontales y verticales están dadas por las siguientes fórmulas:
θ̅ (s, t) = -tan -1 t̂ x / t̂ y
y
ψ̅ (s, t) = sin -1 t̂ z
donde θ̅ (s, t) y ψ̅ (s, t ) Son los ángulos locales que forma el cuerpo en relación con las direcciones horizontal y vertical, en función de la longitud del arco sy el tiempo t.
Los datos muestran que las cometas voladoras usan dos ondas: una onda horizontal con una gran amplitud y una onda vertical con una amplitud más baja, las cuales pasan sucesivamente por el cuerpo desde la cabeza hasta la cola (imagen No. 2).

Imagen # 2
Estas ondas se forman después de un transitorio inicial cuando la serpiente salta en una postura relativamente recta y luego forma una postura característica en forma de S para deslizarse.
Hay cuatro características de la ondulación del aire que asocian una onda vertical con una horizontal ( 2a ). Primero, la onda vertical tiene frecuencias espaciales y temporales dos veces mayores que la onda horizontal. Esto indica que el cuerpo tiene dos veces más curvas verticales que las curvas laterales ( 2a ,2e ). En segundo lugar, las curvas en U en el cuerpo de una cometa voladora pueden identificarse como cruces por cero en la gráfica del ángulo de plegado ( 2b ). En tercer lugar, estos cruces son máximos de ondas verticales, lo que indica que las ondas horizontales y verticales están desfasadas 90 °. Cuarto, la flexión máxima fuera del plano ocurre en las curvas en U y aproximadamente a la mitad de los segmentos rectos. En las curvas en U, la sección transversal del "ala" de la serpiente se pliega debido al movimiento del cuerpo fuera del plano ( 1c , 1d ).
La forma de las olas que viajan cambian con el tiempo a medida que la cometa se acelera y produce fuerzas aerodinámicas, pero algunas características siguen siendo comunes. La onda horizontal es una sinusoide con una parte superior plana, cuya amplitud (80-120 °) depende del número de períodos espaciales, y un número menor de períodos conduce a ángulos de flexión horizontales más altos. La onda vertical es una sinusoide de pico estrecho con canales amplios con amplitudes que van desde 20 ° a 45 °.
La cuantificación de las características espaciales y temporales de las olas mostró que las cometas usan ondas horizontales con 1-1.5 períodos espaciales y una frecuencia de ondulación de 1-1.7 Hz y ondas verticales con 2-3 períodos espaciales y una frecuencia de ondulación de 2-3.4 Hz.
Hay un componente adicional en la ondulación del aire, que los científicos han llamado la "curva dorsoventral", que representa el movimiento hacia arriba y hacia abajo de la parte posterior del cuerpo en relación con la cabeza. El ángulo de inclinación de esta curva fue de -20 ° a 30 °. La curva dorsoventral siempre estuvo presente en los vuelos observados, pero no tuvo una relación significativa con el número de períodos espaciales.
Para determinar con precisión el grado de influencia de la relación entre las ondas horizontales y verticales, así como la influencia de la flexión dorsoventral en la dinámica del vuelo, los científicos crearon un modelo anatómicamente preciso de una serpiente en vuelo. El control sobre el modelo permite, según los científicos, verificar sistemáticamente cómo los componentes de la ondulación (la amplitud de la onda horizontal, el número de períodos espaciales y la frecuencia de la ondulación) afectan la dinámica de planificación a corto y largo plazo.
La onda horizontal se modela como una sinusoide con un pico plano de gran amplitud, y la onda vertical se modela como una sinusoide de pequeña amplitud:
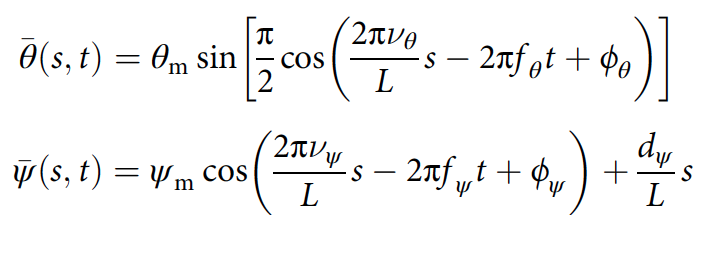
donde θ my ψ m son los ángulos máximos de flexión horizontal y vertical; ν es el número de períodos espaciales; f - frecuencia de ondulación; ϕ - cambio de fase; d ψ - ángulo de flexión dorsoventral; L es la longitud del cuerpo ( 2f , 2g ).
Las ondas horizontales y verticales están conectadas en los datos cinemáticos ( 2e ): ν ψ = 2ν θ , f ψ = 2f θ y ϕ ψ = 2 (ϕ θ- π / 2). Esto simplifica enormemente el modelo a 5 variables que determinan la forma del cuerpo: θ m , ψ m , ν θ , f θ y d ψ .
La posición r = [x, y, z] del cuerpo con respecto al centro de masa se calcula de la siguiente manera: ∂ s x = cosψ̅sinθ̅, ∂ s y = -cosψ̅cosθ̅ y ∂ s z = sinψ̅.
La posición del centro de masa R 0 y la orientación del cuerpo (ángulos de guiñada * , cabeceo y balanceo) se determinan integrando las ecuaciones de movimiento traslacional y rotacional.
Guiñada * : movimientos angulares sobre el eje vertical.
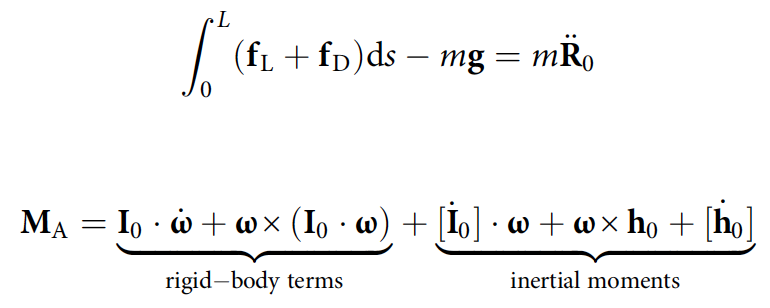
donde f L y f D - fuerzas de elevación y resistencia infinitesimales; M A - momento aerodinámico; m es la masa de la serpiente.
Para confirmar que el modelo matemático da resultados físicamente realistas, los científicos modelaron los vuelos utilizando los parámetros obtenidos durante las observaciones reales de la planificación de serpientes reales (en la imagen a continuación se muestra una comparación de modelado y observaciones).

Imagen # 3
En comparación, el modelo funciona, pero tiene algunas imprecisiones menores que deben corregirse en el futuro.
Para verificar la influencia de la ondulación en las características de planificación, se llevaron a cabo dos simulaciones: con f θ = 0 Hz (sin ondulación) y f θ= 1.2 Hz (frecuencia de ondulación promedio en serpientes). En ambas versiones, ν θ y θ m fueron variadas ( 4a ).

Imagen №4 Los
datos cinemáticos de la forma del cuerpo de la serpiente en el modelo permitieron obtener 121 formas con 1 ≤ ν θ ≤ 1.5 ondas corporales y amplitudes de onda horizontal en el rango de 90 ° ≤ θ m ≤ 119 °. Además, las formas del cuerpo observadas (la parte media del gráfico, separadas diagonalmente; 4b ) se extrajeron de esta matriz . La parte del gráfico que se resalta a continuación contiene las formas del cuerpo "abierto" (que se asemeja a la letra S) y la parte superior - "cerrado" (que se asemeja a un signo de infinito).
La amplitud de la onda vertical y el ángulo dorsoventral se mantuvieron a un nivel constante: 20 ° y 10 °, respectivamente. La simulación se consideró completa cuando el centro de masa de la serpiente tocaba el suelo (aterrizaje) o cuando alguno de los ángulos de orientación excedía el umbral de 85 °. Si esto sucedió, entonces la planificación se consideró inestable, es decir, No es lo mismo que en la naturaleza. Durante la simulación, se probaron tanto la dinámica a corto plazo (altura inicial 10 m) como la dinámica a largo plazo (altura inicial 75 m) con / sin ondulación.
El modelo muestra que la ondulación del aire tiene un efecto positivo en las características de planificación, generalmente aumentando las distancias horizontales y verticales recorridas antes de que la serpiente simulada se vuelva inestable.
Simulación de una serpiente voladora deslizándose con y sin ondulación.
La planificación breve con una altura de lanzamiento de 10 m mostró un buen coeficiente de estabilidad en presencia de ondulación (94%). Si la ondulación no se incluyó en el modelo, entonces solo el 50% de los vuelos fueron estables. La ondulación también aumenta la distancia de deslizamiento (de 4 ma 4,3 m).
Al simular el deslizamiento desde 75 m, la ondulación aumentó la distancia horizontal y vertical antes de que la inestabilidad se manifestara en el 86% de los lanzamientos. En este caso, la ondulación también aumentó la distancia de vuelo en el 92% de los lanzamientos. La ondulación también aumentó la distancia horizontal promedio en 6.9 m.
Para aclarar la influencia de la amplitud de la onda vertical y la flexión dorsoventral en la dinámica de deslizamiento, se utilizaron diferentes valores de estos parámetros en el modelado y se consideraron los resultados.
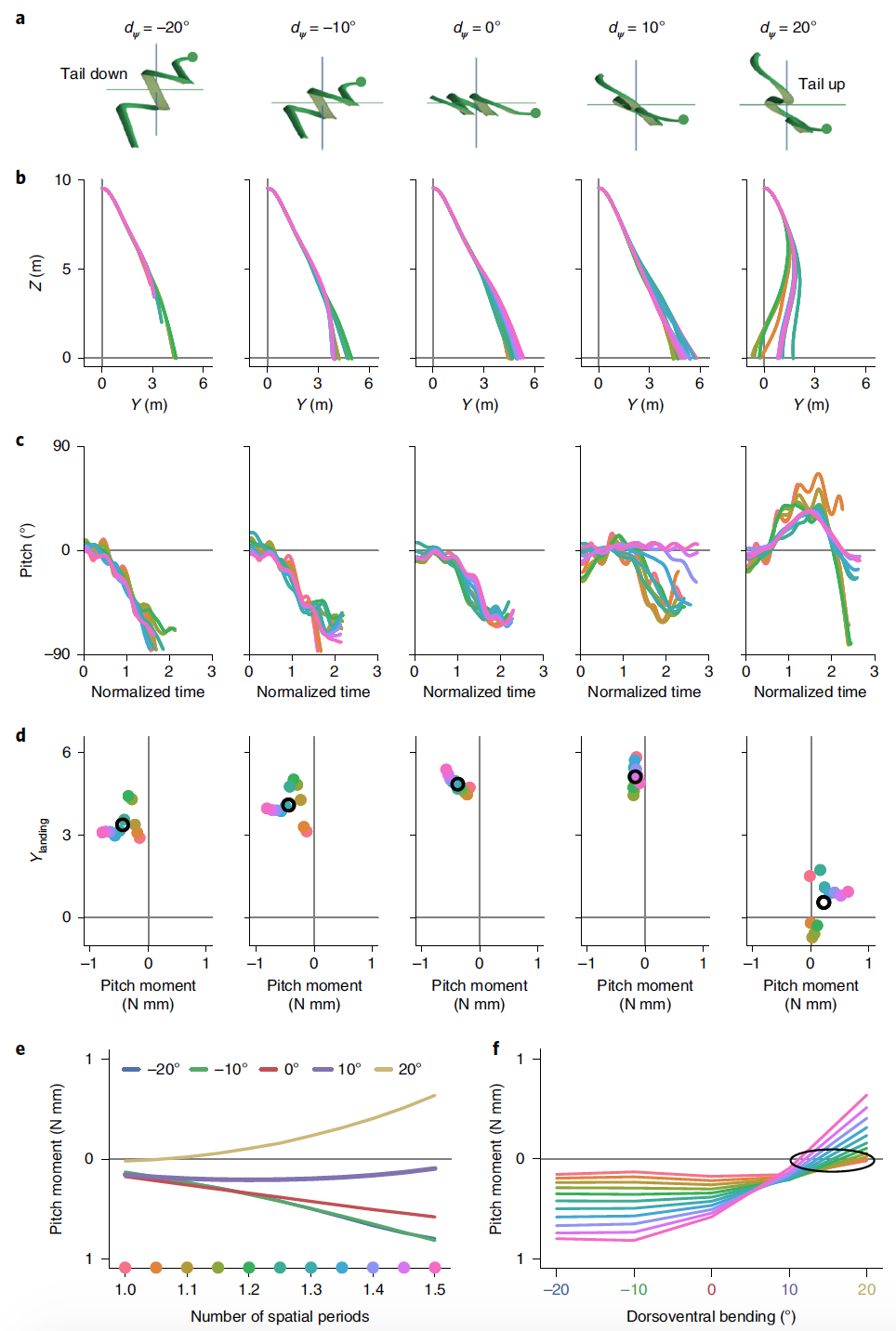
Imagen # 5
Planificación se simuló con ψ m = 0 °, 10 ° y 20 ° y curva dorsoventral de -20 ° a 20 ° en 10 ° pasos ( 5a ) para 11 formas diferentes de cuerpo.
Las vibraciones verticales tienen un efecto relativamente pequeño en la ruta de planificación, mientras que la flexión dorsoventral tiene un efecto significativo.
Una serpiente perfectamente plana (ψ m= 0 °), que nunca se observó durante las pruebas experimentales, mostró los peores resultados esperados. El aumento de la amplitud de la onda vertical aumentó la eficiencia de planificación debido a la torsión de la sección transversal en el plano, proporcionando un ángulo más favorable para crear la fuerza ( 2j ).
En contraste con la amplitud de onda vertical, la curva dorsoventral tuvo un efecto notable en las características de deslizamiento, especialmente en el tono.
En ψ m = -20 ° con la parte posterior del cuerpo por debajo de la cabeza, la planificación no era poco profunda, sino que se volvió inestable en altura antes de caer por 10 m En ψ. M= 20 ° con la parte posterior del cuerpo por encima de la cabeza, la trayectoria es curva hacia atrás, con algunas formas del cuerpo que aterrizan detrás del salto. Tal mala planificación se justifica por una inclinación hacia arriba del cuerpo. Sin embargo, la planificación con los parámetros anteriores tuvo buena estabilidad rotacional.
Para verificar la conexión entre las características de curvatura, inclinación y planificación del cuerpo dorsoventral, se realizó una simulación sin rotación. En lugar de resolver un sistema no lineal acoplado de ecuaciones # 4 y # 5, los científicos tomaron muestras de las fuerzas aerodinámicas en diferentes fases del cuerpo durante el ciclo de ondulación. Luego, la ecuación # 4 se integró aquí, y se calculó la posición y la velocidad del centro de masa.
De hecho, esta manipulación es un experimento de un "túnel de viento virtual", en el que el modelo dinámico se utiliza para calcular las fuerzas distribuidas que actúan sobre el cuerpo durante su aceleración. Este método le permite eliminar la relación entre el movimiento de traslación y de rotación para cuantificar las contribuciones aerodinámicas e inerciales individuales al movimiento de rotación.
Con un aumento en la curva dorsoventral de -20 ° a 10 °, la posición de aterrizaje de la serpiente simulada aumenta a medida que el tono promedio aumenta en la dirección cero ( 5d ). Con una curva dorsoventral de 20 °, el momento de cabeceo promediado por fase se vuelve positivo y las características de planificación disminuyen.
Para cada ángulo de curvatura dorsoventral, la eficiencia de planificación y el momento oblicuo medio también dependen de la forma utilizada, en particular del número de períodos espaciales y la amplitud de la onda horizontal. Para cualquier forma del cuerpo en el momento de la planificación, la curva dorsoventral tiene un gran efecto en el momento promedio de lanzamiento, y con un aumento en el número de períodos espaciales, los momentos divergen, volviéndose más positivos o negativos dependiendo de d ψ .
Las marcas de los momentos de cabeceo promediados por fase en 5e corresponden a la pendiente ascendente o pendiente mostrada en 5c y el rendimiento de deslizamiento resultante en 5b . A las 5fSe muestra que para las formas del cuerpo con el período espacial más pequeño, el momento de cabeceo promedio será el más pequeño.
A partir de los datos anteriores, se puede suponer que la onda vertical hace que el cuerpo se enrolle fuera del plano, cambiando la orientación local del "ala aplanada" (la forma del cuerpo de la serpiente durante la planificación) usando una corriente de aire. La flexión dorsoventral controla la magnitud y el signo del momento principal aerodinámico que actúa sobre el cuerpo. Una cometa voladora puede controlar el momento de lanzamiento cambiando el ángulo de flexión de la región dorsoventral o la forma de una onda horizontal durante el vuelo.
En consecuencia, la curvatura dorsoventral del cuerpo juega un papel extremadamente importante en la estabilidad de deslizamiento, el aterrizaje exitoso y la capacidad de cambiar la trayectoria de deslizamiento justo durante su ejecución.

Imagen No. 6
El análisis de la fase por promedio le permite cuantificar la contribución relativa de los momentos aerodinámicos e inerciales a la dinámica de planificación.
De las ecuaciones No. 5 se deduce que tanto las fuerzas aerodinámicas como la distribución de masa cambiante afectan la orientación del cuerpo. La contribución aerodinámica ( 6a ) aumenta con el tiempo a medida que aumenta la velocidad, mientras que la contribución inercial ( 6b ) permanece constante. Ambos tiempos son periódicos, y solo el momento de lanzamiento muestra un promedio de fase diferente de cero.
Inicialmente, los momentos de inercia predominan cerca de los ejes de cabeceo y balanceo, pero durante un ciclo similar a una onda, su contribución disminuye rápidamente. Los momentos de guiñada inercial, como regla, son un orden de magnitud mayor que los momentos de guiñada aerodinámica y son mayores que los momentos de inercia alrededor de otros ejes. Los momentos de inercia de guiñada surgen debido a una onda horizontal de gran amplitud y un cuerpo ancho en forma de S. Este resultado sugiere que las cometas voladoras pueden usar la rotación inercial como mecanismo de maniobra.
Para conocer más detalladamente los matices del estudio, le recomiendo que examine el informe de los científicos y los materiales adicionales .
Y aquellos que deseen familiarizarse con el software utilizado para analizar la planificación de una cometa voladora pueden hacer clic en este enlace .
Epílogo
En este estudio, los investigadores utilizaron las últimas técnicas de captura de movimiento y modelado 3D para crear un modelo anatómicamente preciso de una serpiente voladora.
Comprender la dinámica del vuelo de un pájaro también fue una vez difícil, pero no desconcertó a los científicos tanto como lo hace una cometa voladora. En la naturaleza, no hay tantos ejemplos de vuelos sin alas, y todos ellos están asociados con el uso de mecanismos no estándar que permiten al animal planificar y no caer como una piedra al suelo.
En el caso de las cometas voladoras, la ondulación que ocurre en el movimiento de las cometas que se arrastran y nadan juega un papel muy importante. Un mecanismo adicional para la estabilización de la planificación es la corrección del ángulo de flexión dorsoventral del cuerpo. Al combinar estos elementos, las cometas voladoras pueden volar de árbol en árbol, sabiendo exactamente el lugar de la futura plantación.
Los autores de este trabajo creen que sus datos no solo nos permitieron comprender mejor los hábitos de las serpientes de árbol decoradas, sino también obtener inspiración adicional para crear robots con forma de serpiente. Sí, tales robots ya existen. Se arrastran, pueden navegar por superficies difíciles y llegar a lugares difíciles de alcanzar, pero ¿pueden volar?
Con tales consideraciones, nuestro mundo pronto se verá como la ciudad de los automóviles de Matrix, donde criaturas robóticas extremadamente inusuales (y ligeramente aterradoras) se arrastraron a lo largo de las paredes, cuyo propósito era difícil de entender. El deseo de una persona de hacer una versión robótica de todo lo que lo rodea no puede ser sofocado. Esta es nuestra naturaleza: entenderlo todo, saberlo todo, poder crear lo que la naturaleza hizo maravillosamente ante nosotros. Si la serpiente robótica, las arañas, los perros y otros animales robóticos tienen muchos más beneficios que daños, dicha investigación está totalmente justificada.
¡Gracias por su atención, tengan curiosidad y tengan un excelente fin de semana, chicos!
Viernes off-top:
, .
, .
Fuera de la parte superior 2.0:
, :)
, :)
Un poco de publicidad
Gracias por estar con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más contenido interesante? Apóyenos haciendo un pedido o recomendando a amigos, VPS en la nube para desarrolladores desde $ 4.99 , un análogo único de servidores de nivel de entrada, que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2697 v3 (6 núcleos) 10GB DDR4 480GB SSD 1Gbps desde $ 19 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).
Dell R730xd es 2 veces más barato en el centro de datos Equinix Tier IV en Amsterdam? ¡Solo tenemos 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV desde $ 199 en los Países Bajos!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - ¡Desde $ 99! Lea sobre Cómo construir la infraestructura de bldg. clase c con servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?