Clever Geek Handbook

Proyecto de aprendizaje de Python: algoritmo de Dijkstra, OpenCV y UI (Parte 1)

Los laberintos son un rompecabezas común para los humanos, pero son un problema de programación interesante que podemos resolver utilizando métodos de ruta más corta como el algoritmo de Dijkstra.



Recordando el algoritmo de Dijkstra



El algoritmo de Dijkstra es uno de los algoritmos de teoría de grafos más populares. Se utiliza para encontrar la ruta más corta entre nodos en un gráfico dirigido. Comenzaremos con el nodo original y las longitudes de borde conocidas entre los nodos.



Primero, asignamos la distancia desde la fuente a todos los nodos. El nodo s obtiene el valor 0 porque es la fuente; el resto obtiene valores ∞ para comenzar.



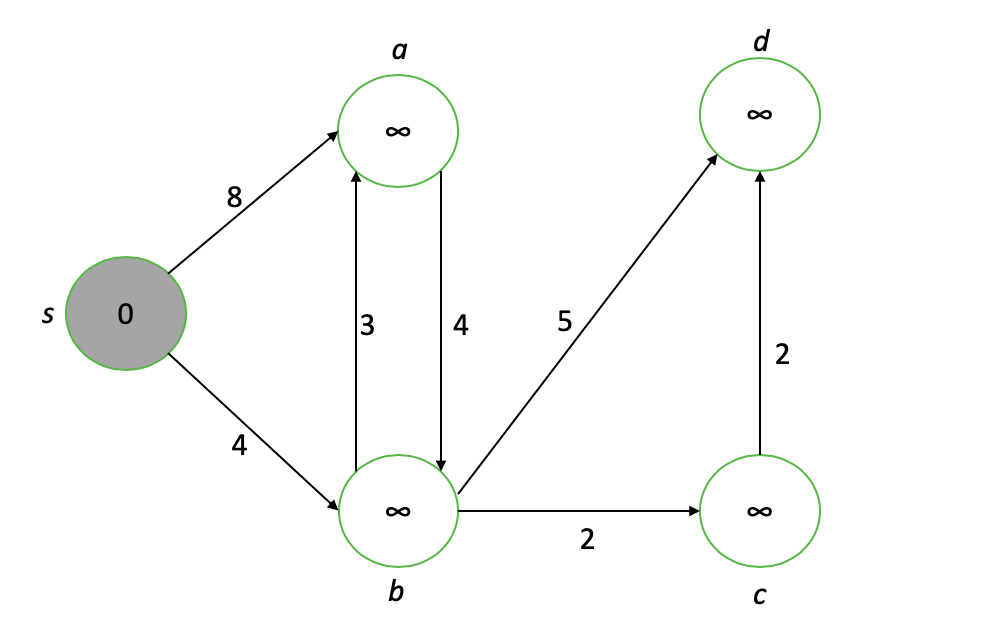
imagen



Nuestro nodo de interés es el nodo sin procesar con el valor más bajo (se muestra en gris), es decir, s. Primero, "debilitamos" cada vértice adyacente a nuestro nodo de interés, actualizando sus valores al mínimo de su valor actual o el valor del nodo de interés más la longitud del borde de conexión ...



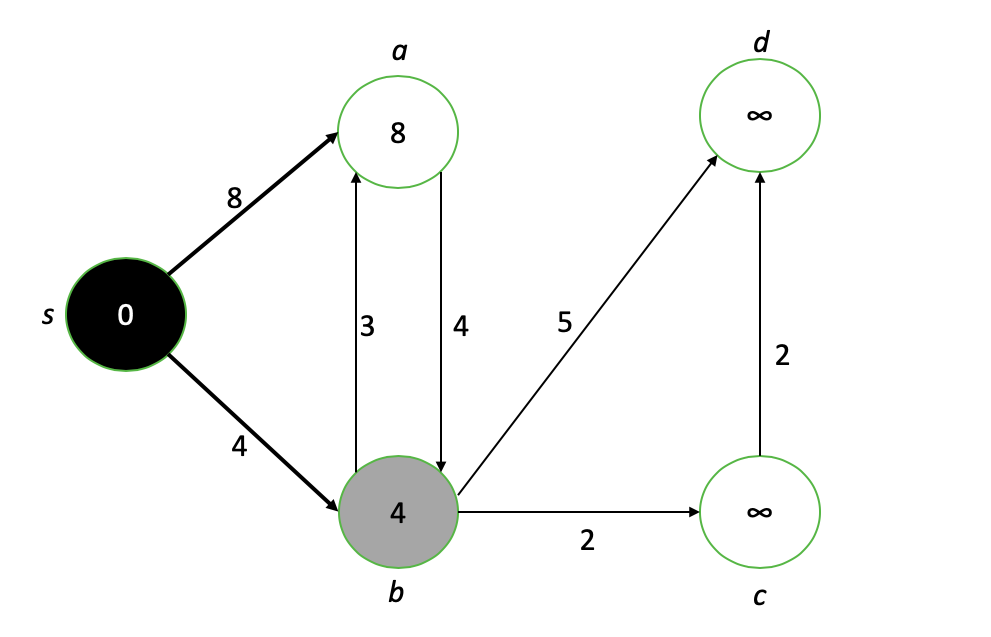
imagen



El nodo s ahora está completo (negro), y sus vecinos ayb tienen sus nuevos valores. El nuevo nodo de interés es b, por lo que repetimos el proceso de "debilitar" a los vecinos de b y finalizar el valor del camino más corto para b.



imagen



Después de pasar por cada nodo, terminamos con un gráfico que muestra la longitud de ruta más corta desde el origen hasta cada nodo.



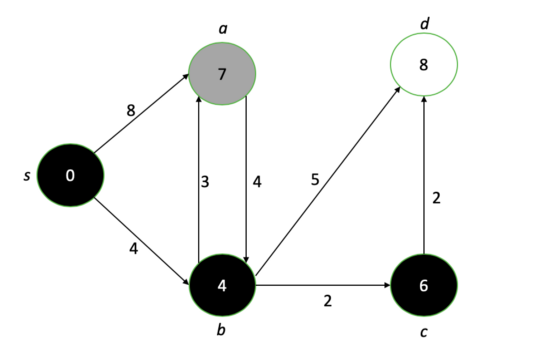
imagen



imagen



imagen



Nuestro diagrama final después de ejecutar el algoritmo de Dijkstra. Los números en cada nodo representan la distancia más corta posible desde el nodo original.



Conceptualización de imágenes de laberintos.



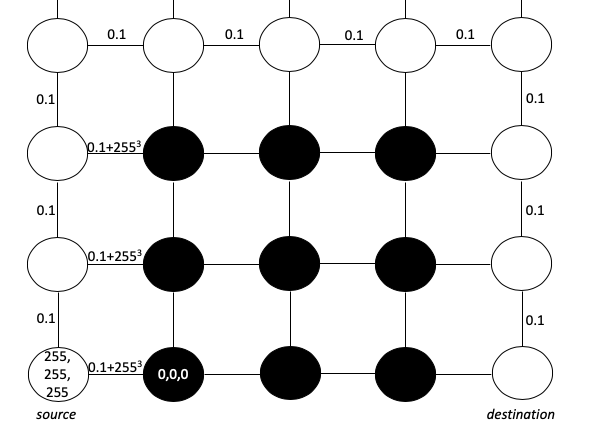
imagen



Podemos imaginar la imagen como una matriz de píxeles. Cada píxel (por simplicidad) tiene un valor RGB de 0,0,0 (negro) o 255,255,255 (blanco). Nuestro objetivo es crear un camino más corto que comience en blanco y no cruce a bordes negros. Para representar este objetivo, podemos considerar cada píxel como un nodo y dibujar bordes entre píxeles adyacentes con longitudes de borde basadas en la diferencia en los valores RGB. Usaremos la fórmula de distancia cuadrada euclidiana y agregaremos 0.1 para asegurar que no haya una longitud de ruta 0 - (requisito para el algoritmo de Dijkstra):



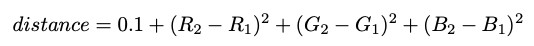
imagen



Esta fórmula hace que la distancia de intersección a través del límite del laberinto sea excesivamente grande. Como podemos ver, el camino más corto desde el origen hasta el destino claramente atravesará la barrera y no a través de ella.



imagen



Implementación



Podemos usar OpenCV, la popular biblioteca de visión de Python para Python, para extraer valores de píxeles y mostrar nuestras imágenes de laberinto. También definamos las coordenadas de nuestras ubicaciones de inicio y final agregando puntos a nuestro laberinto 



import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()


imagen


Creamos una clase Vertex para ayudarnos a rastrear coordenadas. También queremos rastrear el nodo principal para que podamos restaurar la ruta completa tan pronto como encontremos los valores de distancia. 



class Vertex:
    def __init__(self,x_coord,y_coord):
        self.x=x_coord
        self.y=y_coord
        self.d=float('inf') #current distance from source node
        self.parent_x=None
        self.parent_y=None
        self.processed=False
        self.index_in_queue=None


Necesitamos crear una matriz de vértices que represente la disposición bidimensional de los píxeles en la imagen. Esta será la base del algoritmo de Dijkstra. También mantenemos una cola con un montón mínimo de prioridades para el seguimiento de nodos sin procesar. 



def find_shortest_path(img,src,dst):
    pq=[] #min-heap priority queue
    imagerows,imagecols=img.shape[0],img.shape[1]
    matrix = np.full((imagerows, imagecols), None) 
    #access matrix elements by matrix[row][col]
    #fill matrix with vertices
    for r in range(imagerows):
        for c in range(imagecols):
            matrix[r][c]=Vertex(c,r)
            matrix[r][c].index_in_queue=len(pq)
            pq.append(matrix[r][c])
    #set source distance value to 0
    matrix[source_y][source_x].d=0
    #maintain min-heap invariant (minimum d Vertex at list index 0)
    pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)


Necesitamos algunas funciones de ayuda que nos ayuden a encontrar bordes y la longitud de los bordes entre vértices: 



#Implement euclidean squared distance formula
def get_distance(img,u,v):
    return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
    shape=mat.shape
    neighbors=[]
    #ensure neighbors are within image boundaries
    if r > 0 and not mat[r-1][c].processed:
         neighbors.append(mat[r-1][c])
    if r < shape[0] - 1 and not mat[r+1][c].processed:
            neighbors.append(mat[r+1][c])
    if c > 0 and not mat[r][c-1].processed:
        neighbors.append(mat[r][c-1])
    if c < shape[1] - 1 and not mat[r][c+1].processed:
            neighbors.append(mat[r][c+1])
    return neighbors


Ahora podemos implementar el algoritmo de Dijkstra y asignar valores de distancia (d) a todos los vértices de píxeles en la imagen del laberinto: 



while len(pq) > 0:
    u=pq[0] #smallest-value unprocessed node
    #remove node of interest from the queue
    pq[0]=pq[-1] 
    pq[0].index_in_queue=0
    pq.pop()
    pq=bubble_down(pq,0) #min-heap function, see source code 
    
    u.processed=True
    neighbors = get_neighbors(matrix,u.y,u.x)
    for v in neighbors:
        dist=get_distance(img,(u.y,u.x),(v.y,v.x))
        if u.d + dist < v.d:
            v.d = u.d+dist
            v.parent_x=u.x #keep track of the shortest path
            v.parent_y=u.y
            idx=v.index_in_queue
            pq=bubble_down(pq,idx) 
            pq=bubble_up(pq,idx)


Ahora podemos llamar a la función de ruta más corta y dibujar la solución en nuestro laberinto: 



img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen 
plt.show()


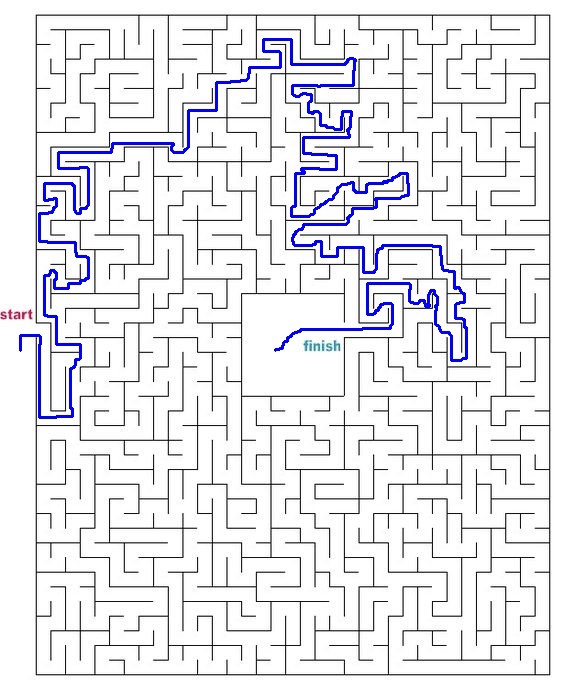
imagen



imagen



Probemos otros laberintos de todo internet.



imagen



imagen



imagen



imagen



El código fuente completo está disponible en GitHub aquí .



Continuación: un proyecto de capacitación de Python: una interfaz con 40 líneas de código (parte 2)



imagen



Obtenga más información sobre cómo obtener una profesión buscada desde cero o subir de nivel en habilidades y salario tomando cursos en línea pagados de SkillFactory:










More articles:


All Articles